Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化)

Courseraの機械学習コースの3週目です。ロジスティック回帰と正則化について学びます。Andrew先生曰く、ここまで学べばシリコンバレーで稼いでいる人たちより深く機械学習を理解しているらしいです。
記事「Coursera機械学習入門オンライン講座虎の巻(文系社会人にオススメ)」を最初に読むことをお勧めします。

サマリ

実績時間：約6.5時間
目安時間：約6時間(正確には時間358分)
※コースに各章の時間目安が書かれています。

一覧

No.	章	目安時間	内容
1.	Logistic Regression	109分	ロジスティクス回帰
1.1	Classification and Representation	37分	分類とその表現方法
1.2	Logistic Regression Model	43分	ロジスティクス回帰のモデル
1.3	Multiclass Classification	9分	多クラス分類
1.4	Review	20分	ロジスティック回帰のレビュー。難しかった。
2.	Regularization	249分	正則化
2.1	Solving the Problem of Overfitting	49分	過学習への対応
2.2	Review	200分	正則化のスライド・クイズとロジスティック回帰・正則化のプログラム演習

講義内容

1. Logistic Regression

1.1. Classification and Representation

1.1.1. Classification

Video:8分, Reading:2分
分類(Classification)の基礎。
分類には、二値分類(Binary Classification)と他クラス分類(Multiclass Classification)があります。
ちなみにロジスティック回帰(Logistic Regression)は「回帰」という単語を含みますが、分類の手法です。

1.1.2. Hypothesis Representation

Video:7分, Reading:3分
仮説の表現。
二値分類で目的変数を0と1に分類する場合、正解ラベルとしては $y\in{0,1}$ で、仮説としてとり得る値範囲は$ 0 \leq h_\theta(x) \leq 1$です。
仮説にシグモイド(Sigmoid)関数を使うと以下の計算式です。
「シグモイド(Sigmoid)関数」と「ロジスティック(Logistic)関数」は同じ意味。

h_\theta(x)= g(\theta^T x) \\
z = \theta^T x \\
g(z) = \frac{1}{1+e^{-z}}

グラフ上で以下の値をとります。

$h_\theta(x)$は確率を示します。例えば$h_\theta(x) = 0.7$の場合は1である確率が70%です。数式で表すと下記の通りです。

h_\theta(x)= P(y=1|x;_\theta)

※ちなみに不等号の下に棒が1本($\leq$)でも2本($\leqq$)でも同じ意味らしいです。中高では常に2本でしたが、大学になると1本な模様。「高校数学の美しい物語」より。

1.1.3. Decision Boundary

Video:14分, Reading:3分
決定境界について。
まず、前提。

h_\theta(x) \geq 0.5 \rightarrow y = 1 \\
h_\theta(x) \lt 0.5 \rightarrow y = 0 \\

zの値が0以上の場合は$g(z)$の値は0.5以上となり、分類(y)は1。

when \quad z \geq 0 \\
g(z) \geq 0.5

zを詳しく書くと。

when \quad \theta^T x \geq 0 \\
g(\theta^T x) \geq 0.5

決定境界を求める例。

\theta =  \left(
    \begin{array}{ccc}
      5  \\
      -1  \\
      0 
    \end{array}
  \right)\\
y=1 \quad if \quad 5+(−1)x_1+0x_2 \geq 0 \\
5−x_1 \geq 0 \\
−x_1 \geq −5 \\
x_1 \leq 5

決定境界は下のスライドのように非線形でも表現できる。

1.2. Logistic Regression Model

1.2.1. Cost Function

Video:10分, Reading:3分
ロジスティック回帰のコスト関数です。
以下の式で表します。正解(y)が1なのに0と間違えると$\infty$に近い誤差を出し、ペナルティを大きくします。逆もまた然りです。

J(\theta) = \frac{1}{m} \sum_{i=1}^{m} Cost(h_\theta(x^{(i)},y^{(i)})) \\
Cost(h_\theta(x),y = -\log(h_\theta(x))) \qquad if \quad y = 1 \\
Cost(h_\theta(x),y = -\log(1 - h_\theta(x))) \qquad if \quad y = 0 \\

1.2.2. Simplified Cost Function and Gradient Descent

Video:10分, Reading:3分
コスト関数の単純化と最急降下法。
「1.2.1. Cost Function」で2行で表現していたコスト関数を1行で表すと以下の式です。これはyを1か0で条件分岐していたのを統合したものです。

Cost(h_\theta(x),y) = -y \quad \log(h_\theta(x))) - (1 - y) \log (1 - h_\theta(x)))\\

これによりコスト関数を1行で表せます。

J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} [y^{(i)}\quad\log(h_\theta(x^{(i)}))) + (1 - y^{(i)}) \log (1 - h_\theta(x^{(i)})))] \\

ベクトル化した実装は以下のとおりです。

h = g(X\theta) \\
J(\theta) = \frac{1}{m} (-y^T \log(h) - (1 - y)^T \log(1 - h))

パラメータを以下のように更新していきます。これは線形回帰と同じです。
なぜこの式になるかは、記事「【機械学習】Stanford University Machine Learning / Week3【学習メモ】」の最後で書いてくれています。

\begin{align*} & Repeat \; \lbrace \newline & \; \theta_j := \theta_j - \frac{\alpha}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} \newline & \rbrace \end{align*}

1.2.3. Advanced Optimization

Video:14分, Reading:3分
最急降下法以外の高度なオプティマイザーとして”Conjugate gradient”(共役(きょうやく)勾配法、”BFGS”、”L-BFGS”を紹介。それらはLearning Rateを手動で決めておく必要もなく、最急降下法より収束が速いことが多い。一方で複雑な処理なので、具体的な説明は今回の講座の対象外。

1.3. Multiclass Classification

1.3.1. Multiclass Classification: One-vs-all

Video:6分, Reading:3分
多クラス分類についてです。
下図のように3クラスに分類する場合は、3つの決定境界を引きます。1クラスを他クラスと識別するためOne-vs-allとも呼ぶようです。

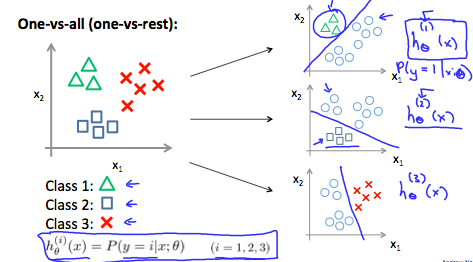
1.4. Review

1.4.1. Lecture Slides

Reading:10分
ここまでのスライドPDFです。

1.4.2. Logistic Regression

Quiz:5問, Reading:10分
ロジスティック回帰のレビュー。
今までのレビューで一番難しかったです(ただ、本当に難しいというより私の理解度がいまいちなのが原因)。5回ほどやり直しました。
3回間違えると8時間再挑戦できなくなります。

2. Regularization

2.1. Solving the Problem of Overfitting

2.1.1. The Problem of Overfitting

Video:9分, Reading:3分
過学習(Overfitting)についてです。
学習が進んでいない状態はUnderfittingまたはHigh Biasと言い、逆に学習しすぎは過学習(Overfitting)またはHigh Varianceと呼びます。
過学習を防ぐために以下の方法があります。

• 特注量を減らす
  • 手動で特徴量を減らす
  • モデルを選択するアルゴリズムの適用
• 正則化(Regularization)
  • 特徴は残すが、$\theta_j$の大きさを減らす
  • 多くの特徴がある場合、正則化(Regularization)は効果的に働く

2.1.2. Cost Function

Video:10分, Reading:3分
正則化(Regularization)を含めたコスト関数についてです。
パラメータが増えた場合にペナルティを加えます。その際に、$\lambda$という正則化パラメータ(Regularization Parameter)を使ってペナルティの多寡を調整できるようにします。

min_\theta \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)} )^2 + \lambda \sum_{j=1}^n \theta_j^2  

正則化パラメータ(Regularization Parameter)の$\lambda$が大きすぎる場合には、Underfittingが起きます。

2.1.3. Regularized Linear Regression

Video:10分, Reading:3分
正則化した線形回帰。
パラメータの$\theta_0$は、最適化の式で独立させます。これは、正則化のペナルティ対象外とするためです。その結果、以下の式により最適化をします。

\begin{align*} & \text{Repeat}\ \lbrace \newline & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \newline & \ \ \ \ \
theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\newline & \rbrace \end{align*}

パラメータ$\theta_j$に関する式を変形できます。

\theta_j := \theta_j (1-\alpha \frac{\lambda}{m})- \alpha \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}

正規方程式(Normal Equation)で解くとこんな感じです。

\begin{align*}& \theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty \newline& \text{where}\ \ L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}\end{align*}

2.1.4. Regularized Logistic Regression

Video:8分, Reading:3分
正則化したロジスティック回帰について。
コスト関数は以下の式(パラメータ$\theta_0$は除く)。

J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} [y^{(i)}\quad\log(h_\theta(x^{(i)}))) + (1 - y^{(i)}) \log (1 - h_\theta(x^{(i)})))] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2  \\

2.2. Review

2.2.1. Lecture Slides

Reading:10分
正則化(Regularization)のスライドPDF。

2.2.2. Regularization

Quiz:5問, Reading:10分
正則化(Regularization)のテスト。
そんなに難しくなかったため、今度は1度で合格。80%ではありましたが・・・

2.2.3. Logistic Regression

Programming Assignment:3時間
ロジスティック回帰の正則化なしとありをOctave/MATLABで実装です。
とても難しいとは思わないのですが、時間短縮のためにGitHubでカンニングしてしまいました
カンニング結果を理解しながら進めてはいますが、ゼロからやった人に比べると理解はだいぶ落ちるはずです。その代わりに40分程度で終わらせることができました。

感想

理解に時間がかかる内容も増え、何度か聞き直すことも多くなってきました。Quizもやり直しやプログラミング演習もカンニングと駄目学生一直線な気がします。このやり方でいいのかわからないですが、まずは終わらせることへ一直線で行きたいと思います。

関連記事

私より詳しくまとめてくれています。

• 【機械学習】Stanford University Machine Learning / Week3【学習メモ】
• Coursera Machine Learning (3): ロジスティック回帰、正則化
• カンニング用GitHub

他の週のリンクです。

• Coursera機械学習入門コース(1週目 - 線形回帰と線形代数)
• Coursera機械学習入門コース(2週目 - 重回帰、多項式回帰、正規方程式)
• Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化) <- 本記事
• Coursera機械学習入門コース(4週目 - ニューラルネットワーク)
• Coursera機械学習入門コース(5週目 - ニューラルネットワークと誤差逆伝播法)
• Coursera機械学習入門コース(6週目 - 様々なアドバイス)
• Coursera機械学習入門コース(7週目 - SVM)
• Coursera機械学習入門コース(8週目 - 教師なし学習(K-MeansとPCA))
• Coursera機械学習入門コース(9週目 - 異常検知、レコメンデーション)
• Coursera機械学習入門コース(10週目 - ビッグデータ対応)
• [Coursera機械学習入門コース(11週目 - 写真OCR)] (https://qiita.com/FukuharaYohei/items/46c60cf591223915e6b4)