More than 5 years have passed since last update.

Coursera機械学習入門コース(10週目 - ビッグデータ対応)

Last updated at 2019-11-16Posted at 2019-11-06

Courseraの機械学習コースの10週目です。ビッグデータ対応ということで、確率的最急降下法とオンライン学習、MapReduceについて学びます。プログラム演習がなくなり、計算系も少ない内容です。
記事「Coursera機械学習入門オンライン講座虎の巻(文系社会人にオススメ)」を最初に読むことをお勧めします。

サマリ

実績時間：約3.5時間
目安時間：約1.5時間(正確には1時間21分)
※コースに各章の時間目安が書かれていて、それを足しただけです。

一覧

No.	章	目安時間	内容
1.1	Gradient Descent with Large Datasets	35分	ビッグデータに対する最急降下法
1.2	Advanced Topics	26分	オンライン学習と処理並列化
1.3	Review	20分	クイズ

1. Large Scale Machine Learning

1.1. Gradient Descent with Large Datasets

1.1.1. Learning With Large Datasets

Video:5分
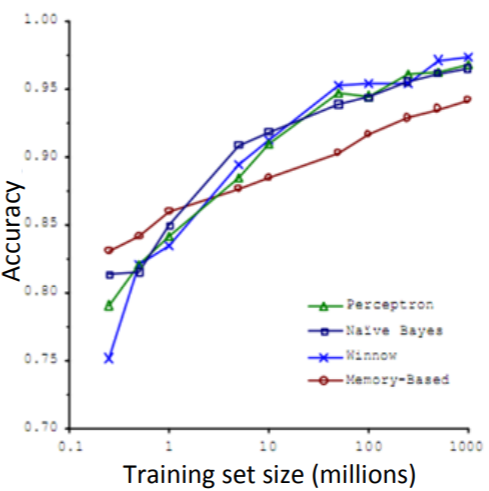
大量データを使って機械学習をする意義について。
6週目で学習した「Data For Machine Learning」の復習ですが、こんな格言？を引用していました。

It’s not who has the best algorithm that wins. It’s who has the most data.

いいアルゴリズムよりも大量データを持つことが勝ちへつながる

ただデータを大量に持つことに注力しすぎずに、本当時必要なことに目を向けることが重要。これも6週目で学習したハイバイアスとハイバリアンスの復習。
ハイバイアス(High Bias)の状態 -> 誤差が大きくてもデータ数を増やすことは解決策にならない

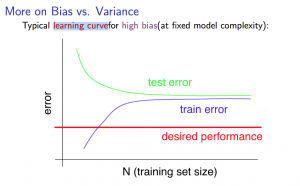
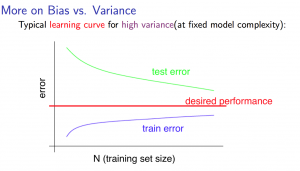
ハイバリアンス(High Variance)の状態 -> 誤差が大きい場合にデータ数を増やすことは解決策になりえる

1.1.2. Stochastic Gradient Descent

Video:13分
確率的最急降下法(Stochastic Gradient Descent)について。
1週目に学習した最急降下法を大量データ向けに変更したのが確率的最急降下法です。オリジナルの最急降下法をバッチ最急降下法(Batch gradient descent)とも呼びます。
バッチ最急降下法は、以下の式でパラメータの更新をしました。

\theta_j := \theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(({h}_\theta(x_i) - y_i)x_{j})

この時にデータ数$m$の値が1億などの大きい数の場合、全データを1回の計算で行い非常に大きな負荷(メモリおよびCPU負荷)がかかります。
これに対して、確率的最急降下法では1回では1データのみに対して計算を行います。具体的には以下のステップを踏みます。

ステップ1. データシャッフル

訓練データをランダムにシャッフル

ステップ2. パラメータ最適化

$i$は訓練データ数、$j$はパラメータ数で、以下の式でパラメータ最適化計算をします。ポイントは1回の計算に1つのデータのみを使うことです。

{ { 
(for \hspace{4pt} i = 1, ..., m ) \hspace{4pt} { \\
\theta_j := \theta_j - \alpha (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}
\hspace{10pt} (for \hspace{4pt} j = 0, ..., n) } \\
}
}

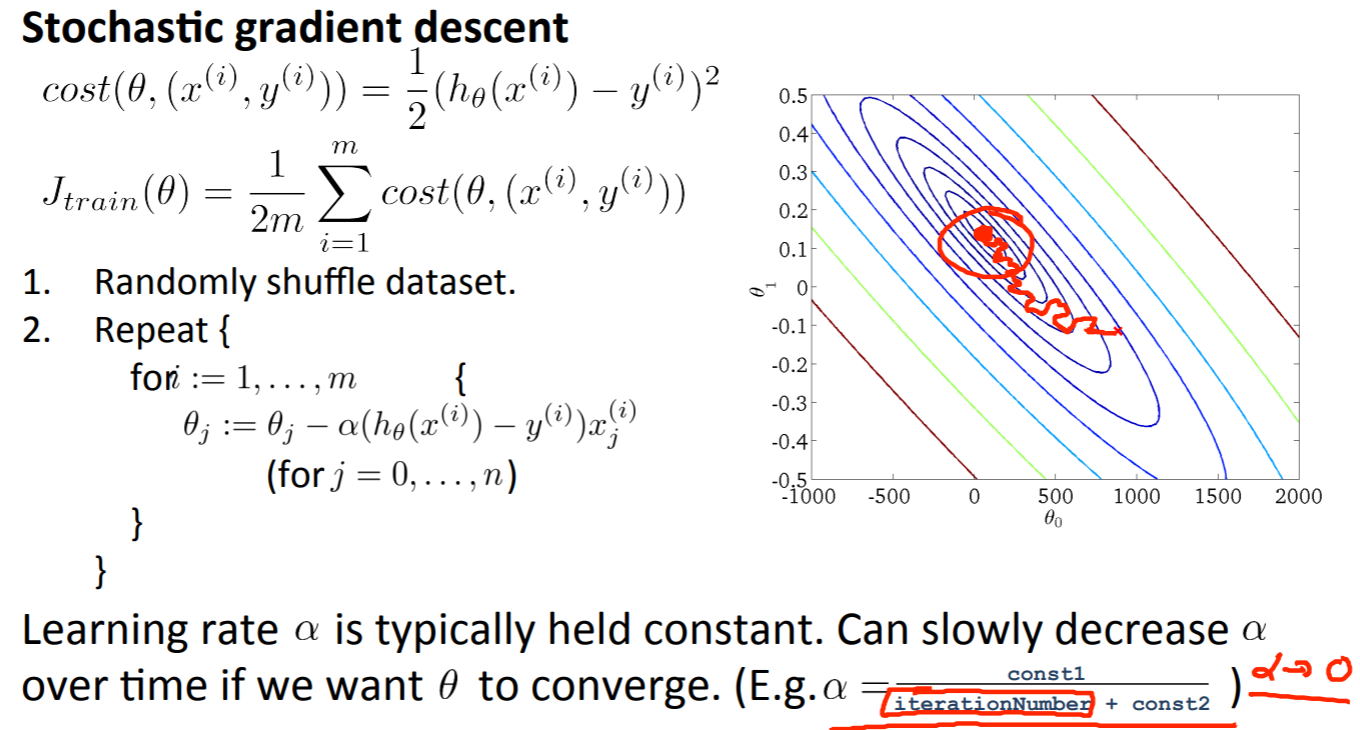
バッチ最急降下法と比較して、収束の際に遠回りをします。これは1データしか使用しないため、間違った方向に進むこともあり得るためです。
※絵を記事「ディープラーニング(深層学習)を理解してみる(勾配降下法：最急降下法と確率的勾配降下法)」から拝借しました。

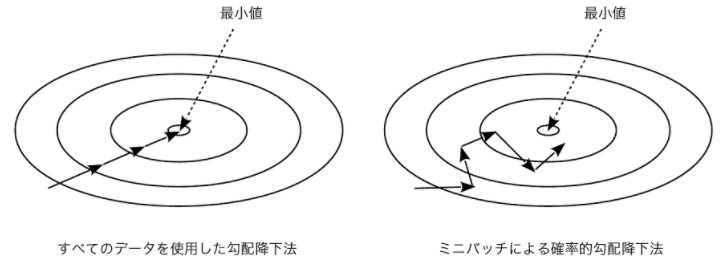
確率的最急降下法は、1データに対する学習を複数回(1から10回程度)行います。ただ、大量データを使った場合には1回でも十分。データ数に依存して1データに対する学習回数を決めます。

1.1.3. Mini-Batch Gradient Descent

Video:6分
ミニバッチ最急降下法(Mini-Batch Gradient Descent)についてです。
バッチ最急降下法と確率的最急降下法のハイブリットな方法で、ミニバッチ最急降下法があります。確率的最急降下法はデータ１件ごとにパラメータを更新していきましたが、ミニバッチ最急降下法はデータN件ごとに同じことを行います。

1.1.4. Stochastic Gradient Descent Convergence

Video:11分
確率的最急降下法が正しく収束しているかを確認する方法についてです。
確率的最急降下法のコスト関数は以下で計算します。

{J(\theta) = \frac{1}{m}\sum^m_{i=1}cost(\theta, (x^{(i)}, y^{(i)}))\\
cost(\theta, (x^{(i)}, y^{(i)}))=\frac{1}{2}(h_\theta(x^{(i)}-y^{(i)})^2)
}

バッチ最急降下法では、コストをトレーニングデータ全体に対して計算していたのに比べて、確率的最急降下法はデータ１件に対して計算します。そして、コスト計算をする対象データは、未学習の次のデータ１件に対して行います。
そして、N(1000など)件ごとにコスト平均した値をグラフ上にプロットして確認します。

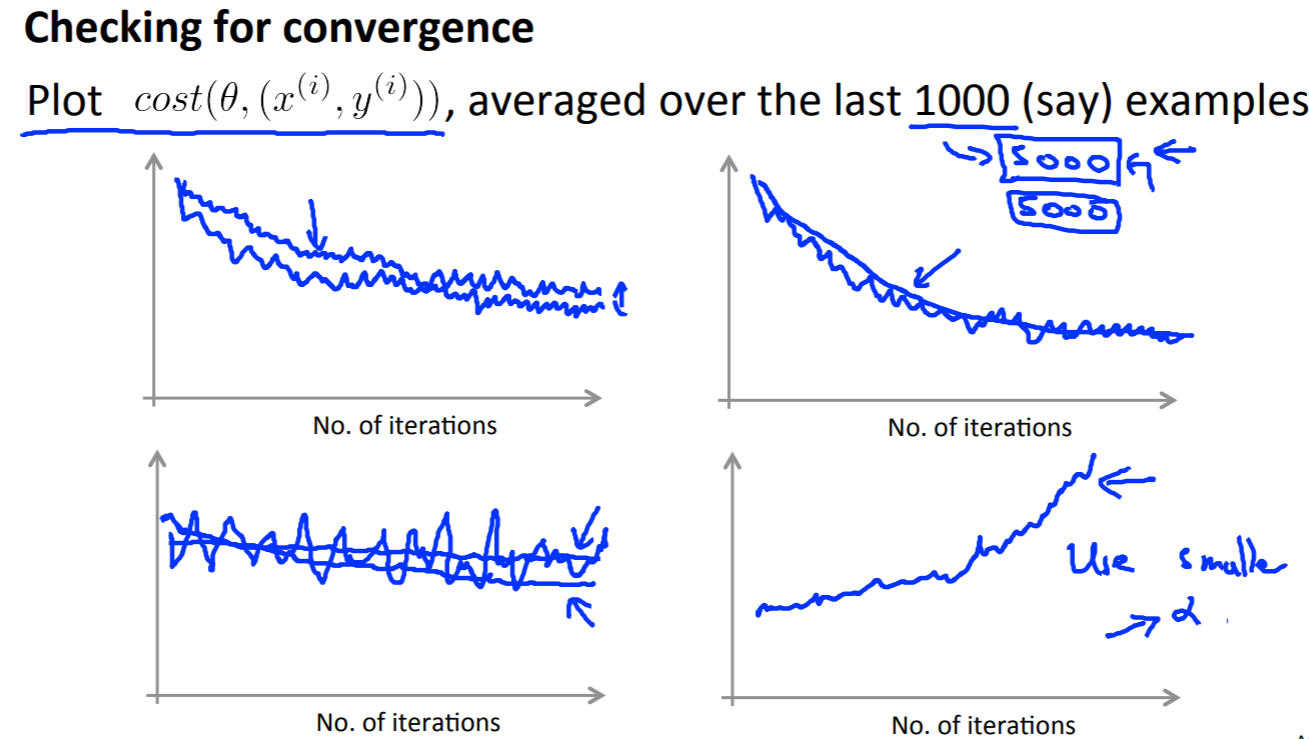
確率的最急降下法では通常、学習率(Learning Rate)$\alpha$を固定させます。確率的最急降下法の特性上、トレーニングデータの最後の方で完全にコスト最小値で収束しにくいので学習率を低下させていく方法を採ることもあります。その場合の学習率は以下の計算式で算出します。

{\alpha = \frac{constant 1}{iterationNumber + constant 2}}

上記の学習率を逓減させていく方法は、あまり採用されないようです。2つの定数値を調整する手間がかかるからです。

1.2. Advanced Topics

1.2.1. Online Learning

Video:12分
オンライン学習について。
E-Commerceサイトでのユーザの閲覧・購買などのデータがストリーミングしてくる系に関する学習です。このような場合は、常に新鮮なデータが来るのでオンラインで(リアルタイムに)学習させます。
求める結果を$y=1$とし、特徴量$x$とパラメータ$\theta$を使って、$y=1$となる確率を考えます。

p(y=1 | x; \theta)

例えば、E-Commerceサイトでのユーザの購入を$y=1$として、ユーザ属性や価格などを$x$とします。これによって購買確率の高い商品をページ上に目立つように掲載させます。
オンライン学習時には、訓練データ$(x^{(train)}, y^{(train)})$は、$(x^{(i)}, y^{(i)})$ではなく、$(x, y)$で表します。これは、1回使った過去データは二度と学習に使わずに、常にストリーミングしてくるデータのみで学習し続けるからです。

1.2.2. Map Reduce and Data Parallelism

Video:14分
MapReduceと並列化について。
Hadoopに代表されるNapReduceを使うことで処理の並列化ができます(処理並列化の対象処理は機械学習に限りません)。トレーニングデータを分割し、それぞれのサーバで計算をさせます。最終的にはどこかのサーバで個々の計算結果を統合します。

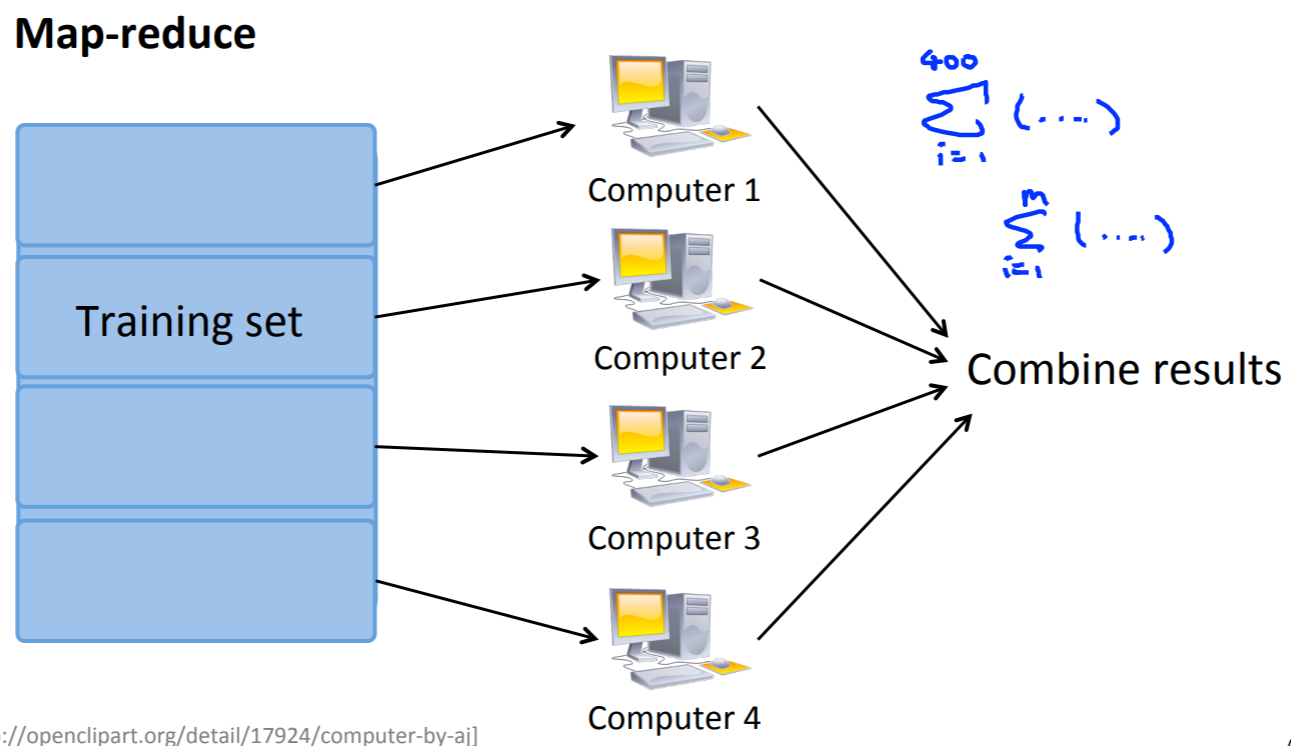
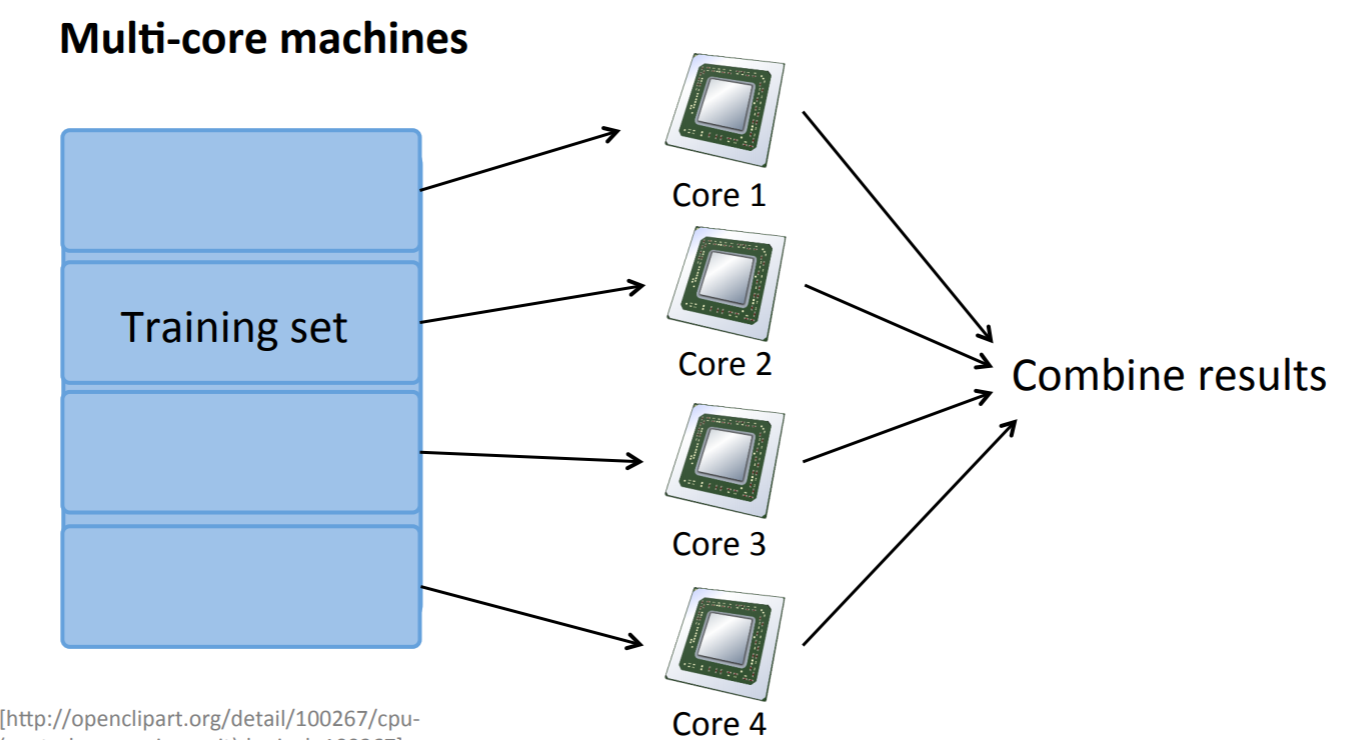
また、マルチコアのサーバ(PC)で処理することでも処理高速化が図れます。優れたライブラリでは、特にプログラム上で意識をせずにマルチコアを有効活用して計算してくれます。

1.3. Review

1.3.1. Lecture Slides

Reading:10分
スライドPDF。

1.3.2. Large Scale Machine Learning

Reading:10分
計算もないので簡単です。
80%の1回目で合格(MapReduceの意味を正確に理解していなかった？)。

感想

ビッグデータ対応に役に立つ内容ということで、そんなに計算系もなくすっきり学べました。プログラム演習もなく理解がしやすかったです。残すところもあと1週です。

私より詳しくまとめてくれています。

他の週のリンクです。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up