機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第十弾は、**大規模機械学習 (Large Scale Machine Learning)**です。ビッグデータを扱わなくなったときにどうしたらいいか、ざっくり学んでいきます。
過去の記事
Coursera Machine Learning (1): 機械学習とは?単回帰分析、最急降下法、目的関数
Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式
Coursera Machine Learning (3): ロジスティック回帰、正則化
Coursera Machine Learning (4): ニューラルネットワーク入門
Coursera Machine Learning (5): ニューラルネットワークとバックプロパゲーション
Coursera Machine Learning (6): 機械学習のモデル評価(交差検定、Bias & Variance、適合率 & 再現率)
Coursera Machine Learning (7): サポートベクターマシーン (SVM)、カーネル (Kernel)
Coursera Machine Learning (8): 教師なし学習 (K-Means)、主成分分析 (PCA)
Coursera Machine Learning (9): 異常検知 (Abnomaly Detection)、レコメンダシステム (Recommender System)
なぜビッグデータなのか? (Why big data?)
ビッグデータビッグデータと騒がれて久しい現代ですが、そもそもビッグデータの何が良いのでしょうか。
勝つのは最高のアルゴリズムを持っている者ではない。最も多くのデータを持っている者だ。(It's not who has the best algorithm that wins. It's who has the most data.)
Coursera Machine Learningで複数回紹介される例です。互いに似ている言葉 ('to', 'too', 'two'など)を文脈に合わせて分類する課題で、4つの代表的な分類アルゴリズムの精度を競ったところ、以下のような結果になったそうです。

(Banko & Brill, 2001から出典)
どのアルゴリズムを使っても、データが多ければ多いほどよい分類精度が出るのは同じ。つまり、多くデータを持っている者がよいモデルを作ることができるということです。
それに、データ数が大きいほうがモデルのオーバーフィット (Overfit. High Varianceとも言う)を防ぐことができ、より汎用性のあるモデルが期待できます。
注意点
当たり前ですが、取ってきたデータ$X$に$Y$を予測するのに十分な情報が含まれていないといけません。意味のないデータをいくら取ってきても仕方ありません。
確率的最急降下法 (Stochastic Gradient Descent)
どの機械学習のアルゴリズムであれ、
1: モデル (Model)として仮説関数 (Hypothesis function) を作る。
Y = h_\theta (X)
2: **目的関数 (Cost Function)**を作る。
J(\theta) = \frac{1}{m}\sum^m_{i=1}cost(\theta, (x^{(i)}, y^{(i)}))
3: 目的関数を最小にするモデルパラメーター$\theta$を、最急降下法 (Gradient Descent) などで求める。
repeat \hspace{15pt}
\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)
\hspace{15pt} (for \hspace{4pt} every \hspace{4pt} j = 0, 1, ..., n)
という流れは同じです。
最急降下法は汎用的な学習アルゴリズムですが、パラメーター$\theta$の1回のアップデートにつきデータ数$m$個分すべての誤差を合計するので、ビッグデータ ($m\ge100,000,000$など)になればなるほど計算に時間がかかってしまいます。
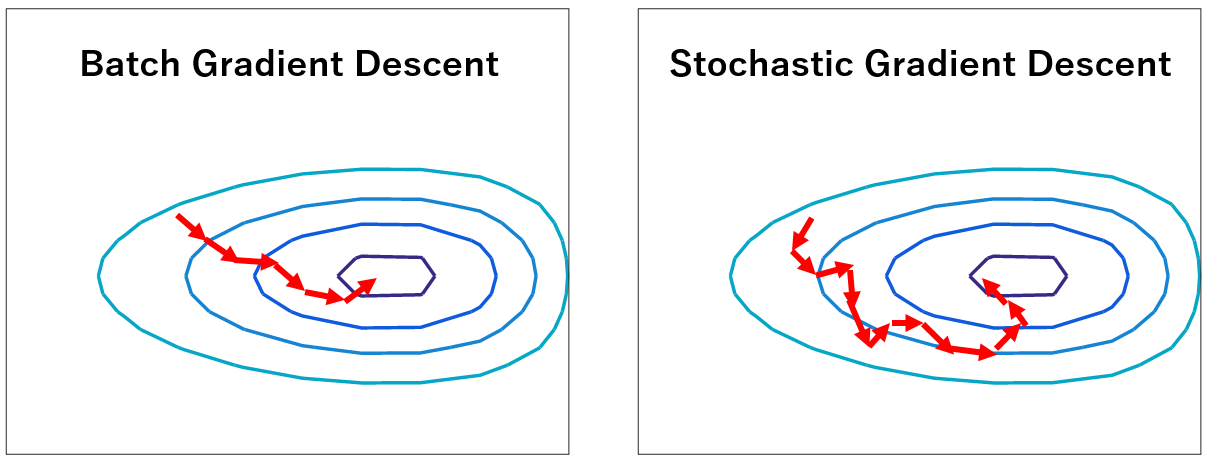
この方法はBatch Gradient Descentといい、時間はかかりますが着実に$J(\theta)$が最小となる$\theta$へ値が収束 (Converge) していきます。
「Batchだと時間かかりすぎるな。もう1回のアップデートで$m$個のデータ全部使うのやめよ。1個でいいや」
というのが、**確率的最急降下法 (Stochastic Gradient Descent)**です。誤差を1回のリピートごとに全てのデータから計算するのではなく、1回のリピートで1つのデータから計算し、それをデータ数$m$回行います。以下のようなアルゴリズムになります。
1: データ$X$のラベルをランダムに入れ替える (Reorder)。
2: $i = 1, ..., m$のループを行う。1回のループ内で、$cost(\theta, (x^{(i)}, y^{(i)}))$を最小にする$\theta_j (j = 0, ..., n)$を計算する。例えば、線形回帰 (Linear Regression)なら以下のようになる。
{
(for \hspace{4pt} i = 1, ..., m ) \hspace{4pt} { \\
\theta_j := \theta_j - \alpha (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}
\hspace{10pt} (for \hspace{4pt} j = 0, ..., n) } \\
}
まず$cost(\theta, (x^{(i)}, y^{(i)}))$を最小にする$\theta$を求め、
次に$cost(\theta, (x^{(i+1)}, y^{(i+1)}))$を最小にする$\theta$を求め、
次に$cost(\theta, (x^{(i+2)}, y^{(i+2)}))$を最小にする$\theta$を求め、......
というように、各データ毎のアップデートを総データ数$m$回繰り返すことで、最終的に全体の目的関数$J(\theta)$を最小にするモデルパラメーター$\theta$に迫ろう!というアルゴリズムが確率的最急降下法です。
各リピートで誤差の総和を計算しない分早いです。ただ、Batch Gradient Descentと違い、リピート毎に目的関数$J(\theta)$は小さくなっていきません。あくまで個別のデータにおける$\theta$のアップデートだからですね。2つを比べると、リピート毎の$J(\theta)$の変化は以下のようなイメージになります。
「さすがに各リピートで1つのデータしか使わないのはよくないか。でも$m$個全部使いたくはないから、そのうちの$b$個を使うことにしよう」
ということもできます。Mini-batch Gradient Descentと呼ばれています。その名の通りですね。
注意点
「Stochastic (Mini-Batch) Gradient Descentが収束しねえ!リピートすればするほど目的関数が大きくなっていくぜ!」という場合は、学習率 (Learning Rate) $\alpha$を小さくします。$\theta$を確実に収束させたければ、リピート回数 (Iteration Number)が大きくなるごとに$\alpha$が小さくなっていくように設計します。例えば、以下のようにします。
\alpha = \frac{constant 1}{iterationNumber + constant 2}
オンライン学習 (Online Learning)
ネットショッピングなどのサービスですと、ユーザーがひっきりなしにやってきて様々な行動をし、去っていきます。ユーザーの行動や嗜好を予測し、よりよいサービスを提供したいときに、モデルがオンラインで学習してくれるといいですよね。
ユーザーの個人情報などから導出した$X$と、モデルパラメーター$\theta$を用いて、ユーザーがある行動(広告をクリックする、など)をする確率は以下のように表現できます。
p(y=1 | x; \theta)
先ほど学んだ確率的最急降下法 (Stochastic Gradient Descent)と同じ要領で、モデルに学習させればいいですね。あるデータ$(x^{(i)}, y^{(i)})$における目的関数$cost(\theta, (x^{(i)}, y^{(i)}))$を最小にする$\theta$を見つける要領で、新しいデータ$(x_{new},y_{new})$における目的関数$cost(\theta, (x_{new}, y_{new}))$を最小にする$\theta$を探させればいいわけです。
マップリデュース (Map-Reduce)
データが大きいとき、並列処理 (Parallel Computing)が必要かもしれません。まず、データを分割し、各計算単位であるノード (Node)に振り分けます (Map step)。各ノードで担当分の計算をしたのち、元のマスターノードへと値を返し、マスターノードが集約してアウトプットを出力します (Reduce Step)。
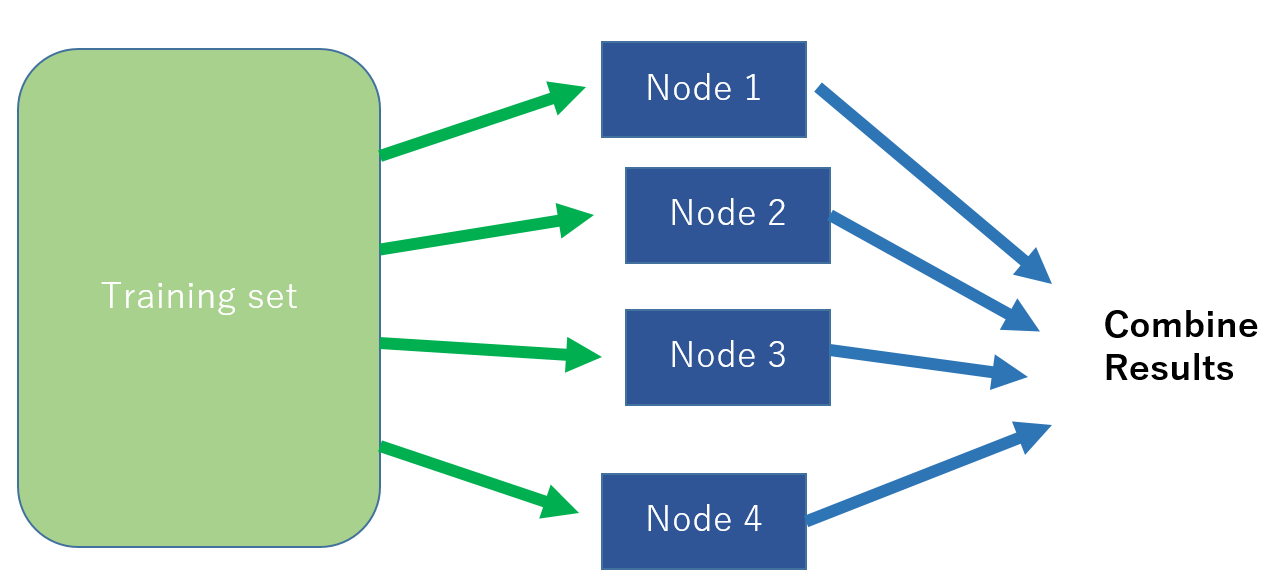
このときのノードは別々のコンピューターであってもいいですが、マルチコア (Multi-Core)CPU内蔵のコンピューターなら各CPUをノードとすることで1台で並列処理することもできます。
まとめのまとめ#
- 意味のあるデータなら、多い方がモデル精度はよくなる。
- 確率的最急降下法やMini-Batch最急降下法は、ビッグデータ向けのモデルの学習手法である。
- オンライン学習は、インターネットサービスなどでデータが日々更新されるときに役立つ。
- Map-Reduceなどの並列処理が、ビッグデータを扱うときには必要になる。
終わりに#
今回は大規模機械学習という、話題のビッグデータに関する話でした。StochasticやMini-BatchのGradient Descentを除くと、あまり具体的な話はありませんでした。プログラミング課題もなかったですし。ビッグデータのイントロ的な内容で、興味があれば自分で調べてみてね!ってことでしょうね。
次回は、最終回。機械学習の応用例として、コンピュータービジョン (Computer Vision)の1ジャンルであるPhoto OCR (Optical Character Recognition) を扱います。機械に写真の中にある文字を認識させようという試みですね。