機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第三弾は、**ロジスティック回帰 (logistic regression)、正則化 (Regularization)**です。のちに学ぶニューラルネットワーク、SVMの土台となる、とても大切なアルゴリズムです。
過去の記事
Coursera Machine Learning (1): 機械学習とは?単回帰分析、最急降下法、目的関数
Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式
ロジスティック回帰 (Logistic Regression)
回帰分析 (Regression)は、ある目的変数$Y$の値を、パラメーター$\theta$によって重み付けされた説明変数$X$によって予測する方法でした。$Y$の予測値である仮定関数$h_\theta(x)$は以下のようになります。
h_\theta (x) = \theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n = \theta^{\mathrm{T}} x
ある値を別の要素の線形和によって説明するこの方法は、直感的にもわかりやすいですね。
では、この方法を回帰分析 (Regression)のみならず分類 (Classification)にも使えないでしょうか?
それを可能にするのが、**ロジスティック回帰 (Logistic Regression)**です。
分類とは、例えば腫瘍 (Tumor)の画像データから、その腫瘍が良性 (Benign) か悪性 (Malignant)を判定する課題のことです。アウトプット、目的変数$Y$は、連続した値ではなく$0$か$1$のようなカテゴリーになります。$0$なら良性、$1$なら悪性、といった感じですね。
通常の回帰分析だと、仮定関数$h_\theta(x)$は連続した値を取り、特別範囲が定まっていません。ただ、分類課題においては、少なくとも予測値の値を$0 \le h_\theta (x) \le 1$にしたい。
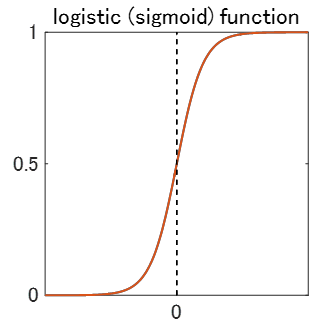
そのために登場するのが、**ロジスティック関数 (Logistic Function)、別名シグモイド関数 (Sigmoid Function)**です。
g(z) = \frac{1}{1 + e^{-z}}
この関数を使えば、$z$にどんな値を入れても、$g(z)$は必ず$0 \le g(z) \le 1$になります。
ロジスティック回帰では、単純に回帰分析の仮定関数$h_\theta (x)$をこの$z$に放り込みます。
h_\theta (x) = \frac{1}{1 + e^{-\theta^{\mathrm{T}} x}}
これがロジスティック回帰における新しい仮定関数で、
- $h_\theta (x) \ge 0.5$なら$y = 1$
- $h_\theta (x) \le 0.5$なら$y = 0$
というように分類判定をします。
さて、この仮定関数$h_\theta (x)$と実際のデータ$Y$との差を最小にする、重み付けパラメーター$\theta$を探すため、目的関数 (Cost function)を導入します。
目的関数 (Cost Function)
回帰分析 (Regression)での目的関数は、以下のようでした。
J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta (x^{(i)}) - y^{(i)})^2
選んだパラメーター$\theta$を用いて計算した予測値$h_\theta (x)$と、実際の値$y$がどれだけずれているのか、二乗差をとって足し合わせ、平均を取っています。要は誤差を計算しているわけですね。
ロジスティック回帰では、例えば0か1のカテゴリーに分類する課題の場合、$y = 0$ or $1$の2値しかとりません。そのため、**$h_\theta (x)$が$y$の値と一致していれば目的関数$J(\theta)$が最小($ \to 0$)になり、$h_\theta (x)$が$y$の値と不一致ならば目的関数$J(\theta)$が最大($\to \infty$)**になるような関数を$J(\theta)$に使う必要があります。
こんなときうってつけな、簡単な関数があります。logに$-$をつけたものです。
$y = 1$なら
J(\theta) = -log(h_\theta (x))
$y = 0$なら
J(\theta) = -log(1 - h_\theta (x))
とすれば、どちらも$h_\theta (x) = y$のとき、log内の括弧の中の値が1になり、$J(\theta) = 0$となります。逆に$y$がもう一方の値だったとき、$J(\theta) \to \infty$となります。
この2つをまとめると、以下のように目的関数を表現できます。これにより、場合分けがいらなくなります。
J(\theta) = - \frac{1}{m} [ \sum_{i=1}^m y^{(i)} log(h_\theta (x^{(i)})) + (1 - y^{(i)}) log(1 - h_\theta (x^{(i)}))]
さて、これで目的関数$J(\theta)$ができました。
これが最小値を取るパラメーター$\theta$を求めるために、最急降下法 (Gradient Descent)というアルゴリズムを使うのは単回帰分析や重回帰分析と一緒です。
最急降下法 (Gradient Descent)
\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta)
= \theta_j - \alpha \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) x_j ^{(i)}
これを、$j = 0, 1, ... , n$それぞれについて同時に、$\theta_j$の値が収束するまで (目安としては、1回のアップデートでの値の変化が$10^{-3}$より小さくなるまで)繰り返します。1回のリピートで、パラメーター$\theta_j$は、(そのときの目的関数$J(\theta)$の傾き) x (学習率$\alpha$) だけ値が変化していきます。
・・・つまり、単回帰分析や重回帰分析となにも変わりません。ロジスティック回帰の場合は、$h_\theta (x)$がロジスティック(シグモイド)関数である点が唯一の違いです。
複数クラスへの分類 (Multiclass Classification)
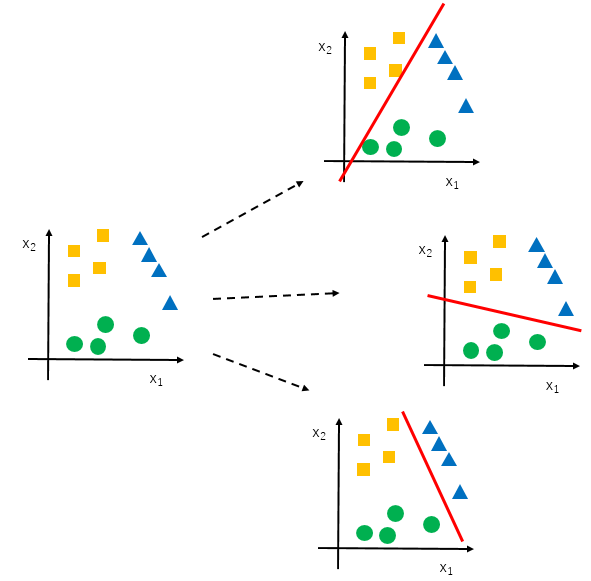
カテゴリーが3とか4のときもありますよね。天気予報などでは、晴れ、曇り、雨、雪と、分類すべきカテゴリーは2つ以上あるのが普通です。こんなとき、ロジスティック回帰では、one vs restあるいはone vs allという方法を取ります。
その名の通り、全てのカテゴリー ($j = 0, 1, ... $)それぞれについて、そのカテゴリー vs その他のカテゴリー と分類するロジスティック回帰モデル$h_\theta ^{(i)} (x)$を作ります。カテゴリーが$n$個あれば、モデルも$n$個できます ($n \ge 3$)。
それぞれのモデルは、
h_\theta ^{(i)} (x) = P (y = i | x; \theta)
というように、$\theta$によってパラメーターづけられたインプット$x$に対して、$y = i$となる条件付き確率を返します。新たなインプット$x_{new}$が与えられたとき、それが属するカテゴリーは、$h_\theta ^{(i)} (x_{new})$が最大となるカテゴリー$i$となります。
オーバーフィッティング (Overfitting)
回帰分析では、仮定関数$h_\theta (x)$は必ずしも直線である必要はありません。説明変数$x$の次数を増やしていけば ($x^2$,$x^3$,...)、データを曲線でフィットすることができます。これを、**多項回帰 (Polynomial Regression)**といいます。
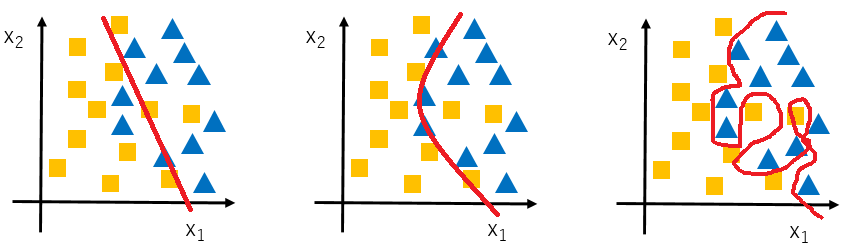
ロジスティック回帰でも同様です。データを分類する**決定境界 (decision boundary)**は、直線のみならず曲線になることができます。
- (左) $h_\theta (x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2)$
- (真ん中) $h_\theta (x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2 + ...)$
- (右) $h_\theta (x) = g(\theta_0 + \theta_1 x_1 + \theta_2 x_1^2 + \theta_3 x_1^2 x_2 + \theta_4 x_1^2 x_2^2 + \theta_5 x_1^2 x_2^3 + \theta_6 x_1^3 x_2 + ...)$
多項回帰を使うと、上記右図のように、手持ちのデータセット (training set)を100%近い精度で説明するモデルを作ることができます。ただ、そのモデルはあまりにもtraining setの説明に特化しているため、新しいデータセット (test set)には全く役に立たないかもしれません。これが、**オーバーフィッティング (Overfitting)**の問題です。
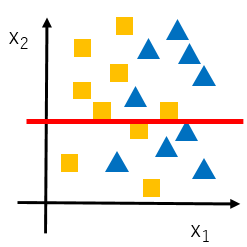
多項回帰が問題なわけではなく、上記左図のように、線形回帰だけだとモデルの精度が悪いことがあります。フィッティングが悪すぎる場合、アンダーフィッティング (Underfitting)と呼ばれます。
オーバーフィッティングでもアンダーフィッティングでもない、汎用性があってかつ精度の高いモデルを作るためには、余計な説明変数を減らしたり、必要な説明変数を増やしたりする他、**正則化 (Regularization)**という方法があります。
正則化 (Regularization)
パラメーター$\theta$の値を十分小さくしてしまえば、説明変数$x$がどんな多項式であっても、その説明変数の予測値$h_\theta(x)$への影響を小さくできるからオーバーフィットしにくくなる、という考えです。
そのために、正則化パラメーター (Regularization Parameter) $\lambda$ を目的関数$J(\theta)$に導入します。
J(\theta) = \frac{1}{2m} [ \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2]
2つ目の$\sum$の項が目的関数$J(\theta)$に入ることにより、$\theta$の値を大きく取ると目的関数が最小値に近づけないように設計しています。
注目したいのは、この2つ目の$\sum$の項の範囲が$j = 1, ..., n$であること、つまり$\theta_0$には$\lambda$がかからないことです。$\theta_0$は説明変数$x$の重み付けをしない、切片 (Intercept)項なので、正則化しなくていいのですね。
この事実は、目的関数$J(\theta)$の最小値を求めるアルゴリズムである最急降下法 (Gradient Descent)にも影響してきます。$\theta_0$のアップデートのときは、正規化パラメーターが介入しないのです。
正則化された最急降下法 (Gradient Descent with Regularization)
\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})x_0^{(i)} \\
\theta_j := \theta_j - \alpha [ \frac{1}{m} \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)})x_j^{(i)} - \frac{\lambda}{m} \theta_j ]
このように、$j \ge 1$のときは正則化された項がアップデートに影響します。収束まで上記アルゴリズムを全ての$j = 0, 1, ..., n$で同時に繰り返すのは、今までと同様です。
注意点
$\lambda$を大きくしすぎると ($\lambda = 10^6$など)、$\theta_0$以外の全ての$\theta$ ($\theta_1$, $\theta_2$, ..., $\theta_n$)が、限りなく$0$に近づきます。すると、$h_\theta (x) \to \theta_0$となり、$h_\theta (x)$はどんなインプット$x$に対しても同じ値$\theta_0$しか返さないため、アンダーフィットになってしまいます。
まとめのまとめ#
- ロジスティック回帰は、回帰分析を分類課題に応用した方法である。
- ロジスティック回帰では、ロジスティック(シグモイド)関数を使うため、目的関数 (cost function)の形が単回帰分析や重回帰分析と異なる。
- 複数カテゴリーへの分類は、one vs allを用いてカテゴリー数だけモデルを作る。
- 正則化により、オーバーフィッティングを防ぐことができる。
終わりに#
ロジスティック回帰は名前こそ回帰ですが、その実は分類課題に対するモデルなんですね。
ここまでくると、Andrew Ng教授曰く「シリコンバレーで機械学習を使って金を荒稼ぎしてる奴らより、君たちの方がよほど機械学習を理解している。おめでとう!」らしいです。いやいや。んなわけねー。
次回はとうとう、ニューラルネットワーク (Neural Network)のお話に入っていきます。