機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第一弾は、機械学習の定義 (What is machine learning?)、単回帰分析 (linear regression)、最急降下法 (gradient descent)、目的関数(cost function) です。
そもそも機械学習ってなに?
機械学習の元々の定義は、
The field of study that gives computers the ability to learn without being explicitly programmed. (Arthur Samuel)
つまり、**「明示的なプログラミングをせず、コンピューターに学習能力を持たせる学問」**です。機械学習のコンピュータープログラムは、ある課題に触れる中で経験から学び、その課題を解く能力が経験によって改善しなければなりません。
あらゆる機械学習は、おおざっぱに2つに分類できます。
教師あり学習 (Supervised Learning)###
あるデータにおいてインプットとアウトプットの関係が明らかな場合、その課題は教師あり学習と呼ばれます。
教師あり学習は、1)**回帰分析 (regression)**と2)**分類 (classification)**に分かれます。
1) 回帰分析 (regression)
インプット$X_1$...$X_n$とアウトプット$Y_1$...$Y_n$の関係がわかっているデータを用いて、新しいインプット$X_a$からアウトプット$Y_a$の具体的な数値を予測する課題のことです。
例)人の写真を見て、その人の年齢(数値!)を予測。
2) 分類 (classification)
インプット$X_1$...$X_n$とアウトプット$Y_1$...$Y_n$の関係がわかっているデータを用いて、新しいインプット$X_a$からアウトプット$Y_a$のカテゴリーを予測する課題のことです。
例)人の写真を見て、その人に恋人がいるかどうか (いる、いないのカテゴリー!) を予測。
教師なし学習 (Unsupervised Learning)###
データに含まれる変数同士の関係を仮定せず、そのデータの構造を決定するとき、その課題は教師なし学習と呼ばれます。
教師なし学習の代表例は、クラスタリング(clustering)です。
クラスタリング (clustering)
データ内の変数に基づき、データを複数の小さなグループに仕分けする。
例)男性の新入社員500人の履歴書を、そこにある変数(専攻、学歴、職歴、趣味など)から、自動的に似た者同士のグループに仕分ける。
単回帰分析 (Linear Regression with One Variable)
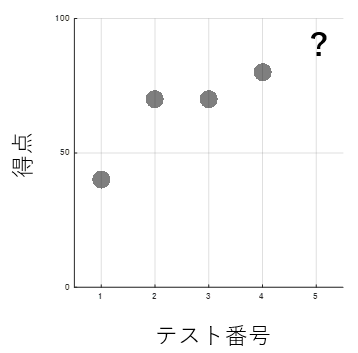
太郎君の過去4回分の数学の試験の得点は、以下のようであったとします。
| テスト番号 | 得点 |
|---|---|
| 1 | 40 |
| 2 | 70 |
| 3 | 70 |
| 4 | 80 |
数学が得意になってきた太郎君は、自分の次の数学の試験の得点を予測しようと試みます。得点、という数値を予測するので、教師あり学習の、回帰分析を使います。今回は単回帰分析という、1つのアウトプット(得点)を1つのインプット(テスト番号)から予測する方法を取ります。
仮定関数 (Hypothesis function)###
テスト番号を$X$、得点を$Y$とすると、単回帰分析では、$Y$は$X$によって以下のような1次関数の式で説明されます。
\hat{Y} = h_\theta (X) = \theta_0 + \theta_1(X)
これが、仮定関数 (hypothesis function)で、答えとなる予測式の鋳型です。この関数の自由パラメーター$\theta_0$、$\theta_1$をいじり、データに最も誤差なくフィットする式を作ります。
目的関数###
仮定関数がどの程度誤差なくデータにフィットしているかを計算するため、目的関数 (cost function)を導入します。
J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^m(\hat{Y}_i - Y_i)^2 = \frac{1}{2m}\sum_{i=1}^m(h_\theta (X_i) - Y_i)^2
パッと見怖そうですが、実際は予測値$\hat{Y} $が実測値$Y$とどれくらいずれているのか、全てのデータポイント (今回は$m = 4$)で差の二乗を計算し、足し合わせて、平均を取っているだけです。2で割られているのは、後々この関数$J(\theta_0, \theta_1)$を微分するときにちょっと計算しやすくするためです。
もし、$J(\theta_0, \theta_1) = 0$となるような$\theta_0$、$\theta_1$を見つけられたなら、仮定関数$h_\theta (X)$は誤差なく、全てのデータポイントを完全に通ることになります。
最急降下法 (Gradient Descent)
仮定関数$h_\theta (X)$と、そのパフォーマンスを定量する目的関数$J(\theta_0, \theta_1)$が決まったところで、実際に$\theta_0$、$\theta_1$を動かしていきます。目的関数$J(\theta_0, \theta_1)$を最小にする$\theta_0$、$\theta_1$を見つける方法の1つが、**最急降下法 (Gradient Descent)**です。アルゴリズムは以下のようになります。
\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta)
= \theta_j - \alpha \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) x_j ^{(i)}
このとき、$j = 0,1$(自由パラメーターのインデックス)で、$\alpha$は**学習率 (learning rate)**と呼ばれます。
ある関数の最小値を求める問題は、高校数学でやるように、微分して傾きを求めますね。今回は変数が$\theta_0$、$\theta_1$と2つあるので、片方は定数として微分する、偏微分を使っています。そうして求められた傾きに、$\alpha$をかけ、それをもともとの$\theta_j$から引くことで、新しい$\theta_j$を求めます。
これを、傾き$\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1)$が十分小さくなるまで繰り返します。
もし0になれば、この関数は**極小値 (local minima)**をとることになります。傾きが0に近づくと、$\alpha$がどんな値であれ、$\theta_j$の変動幅は小さくなり、0に近づいていきます。そうして変動幅が十分小さくなった状態を収束 (Convergence)といい、収束まで上記のアルゴリズムを繰り返します。
収束の目安は、1回のアップデートにおける$\theta_j$の値の変化が$10^{-3}$以下になるときだといわれています。
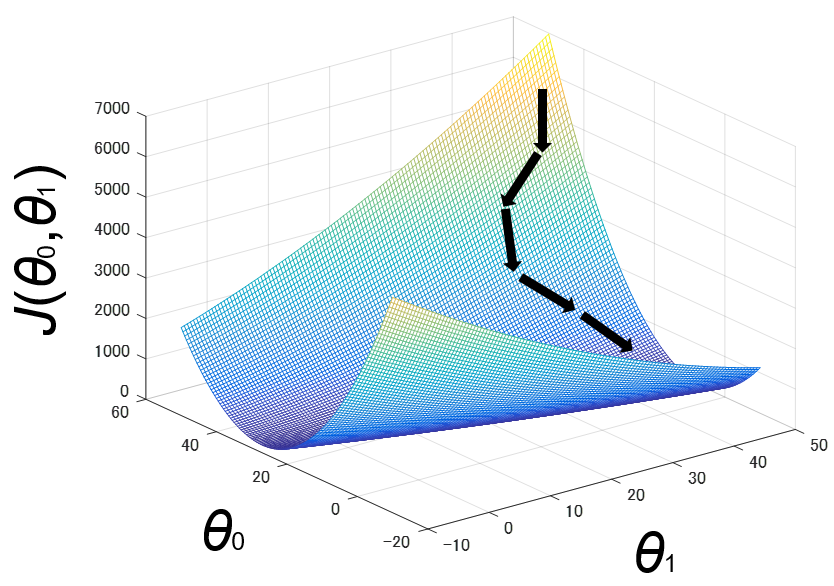
以下は、最急降下法によって、目的関数$J(\theta_0, \theta_1)$の値が収束に近づいていく様子を表しています。
注意点
-
$\theta_0, \theta_1$のアップデートは同時に行います。つまり、まず$\theta_0$をアップデートして、その値を$\theta_1$のアップデートに使う……ということは推奨されないようです。
-
$\alpha$が大きすぎると、$\theta_j$の変動幅が大きすぎ、収束しないことも。逆に$\alpha$が小さいとゆっくりですが、確実に収束していきます。
まとめのまとめ#
- 機械学習は、コンピューターに学習能力を持たせる学問である。
- 機械学習は、教師あり学習(回帰分析、分類)と教師なし学習(クラスタリング)に分かれる。
- 回帰分析では、まず仮説関数を作り、そのパフォーマンスを目的関数で定量化する。
- 目的関数の最小値を求めるため、最急降下法を用いる。
終わりに#
評判通り、CourseraのMachine Learningの講義はわかりやすくまとまってるなぁという印象です。興味はあっても、初心者でいきなりBishopとか読むのは厳しいですよね。まだ始まったばかりですが、期待できそうです。
次回は主に、重回帰分析 (Linear Regression with Multiple Variables)のお話です。