Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式

　機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera　を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。

　第二弾は、重回帰分析 (multiple linear regression)、スケーリング (feature scaling)、正規方程式 (normal equation)です。

過去の記事
Coursera Machine Learning (1): 機械学習とは？単回帰分析、最急降下法、目的関数

重回帰分析 (Linear Regression with Multiple Variables)

　単回帰分析は、1つのアウトプット$Y$を1つのインプット$X$から予測する手法でした。重回帰分析は、$X$が1つのベクトル (vector)ではなく、複数のベクトルの集まり、マトリックス (matrix)になっただけです。

（例）志望校の合格可能性を、各教科の得点から予測する

テスト番号	数学の得点	英語の得点	国語の得点	理科の得点	社会の得点	志望校の合格可能性 (%)
1	40	60	20	10	10	10
2	70	70	60	60	40	30
3	70	90	40	40	60	50
4	80	80	50	90	70	80

　このとき、仮定関数 (Hypothesis Function)は、各教科の点数を$X$、志望校の合格可能性を$Y$とすると、重回帰分析では、$Y$は$X$によって以下のような1次関数の式で説明されます。

\hat{Y} = h_\theta (X) = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3　+\theta_4 x_4+ \theta_5 x_5 = \theta^{\mathrm{T}} X^{\mathrm{T}} 

　このとき、$X$は4行（テスト数）6列（要素が全て1のベクトル + 5教科の得点）のマトリックス、$Y$は4行1列（志望校の合格可能性）のベクトル、$\theta$はそれぞれの説明変数（教科の得点）の重みづけをするパラメーターベクトルです。$\theta^{\mathrm{T}}$の$T$は転置行列 (transposed matrix、つまり、行と列を入れ替えた行列のこと)であることを示しています。

  X = \left[
    \begin{array}{rrr}
      1 & 40 & 60 & 20 & 10 & 10 \\
      1 & 70 & 70 & 60 & 60 & 40 \\
      1 & 70 & 90 & 40 & 40 & 60 \\
      1 & 80 & 80 & 50 & 90 & 70
    \end{array}
  \right]

  Y = \left[
    \begin{array}{rrr}
      10 \\
      30 \\
      50 \\
      80
    \end{array}
  \right]

  \theta = \left[
    \begin{array}{rrr}
      \theta_0 \\
      \theta_1 \\
      \theta_2 \\
      \theta_3 \\
      \theta_4 \\
      \theta_5 \\
    \end{array}
  \right]

　データに最もフィットするような$\theta$を探すために、実データとの誤差を定量化する目的関数 (cost function)と、目的関数の最小値を求めるためのアルゴリズムである最急降下法 (Gradient Descent)を導入します。

目的関数 (Cost Function)

   J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta (x^{(i)}) - y^{(i)})^2

　このとき、$x^{(i)}$は、$i$番目のインプットデータ ($i = 2$なら、$x^{(2)}$はテスト番号2のときの各教科の点数)、$y^{(i)}$は、そのときの志望校の合格可能性 (= 30 [%])を表します。

　例によって、選んだパラメーター$\theta$を用いて計算した予測値$h_\theta (x)$と、実際の値$y$がどれだけずれているのか、二乗差をとって足し合わせ、平均を取っているだけですね。2で割っているのは、最小値を求めるために微分する際、$\sum$の中から来る2と相殺されるようにつけてあります。

最急降下法 (Gradient Descent)

   \theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta)
             = \theta_j - \alpha \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) x_j ^{(i)}

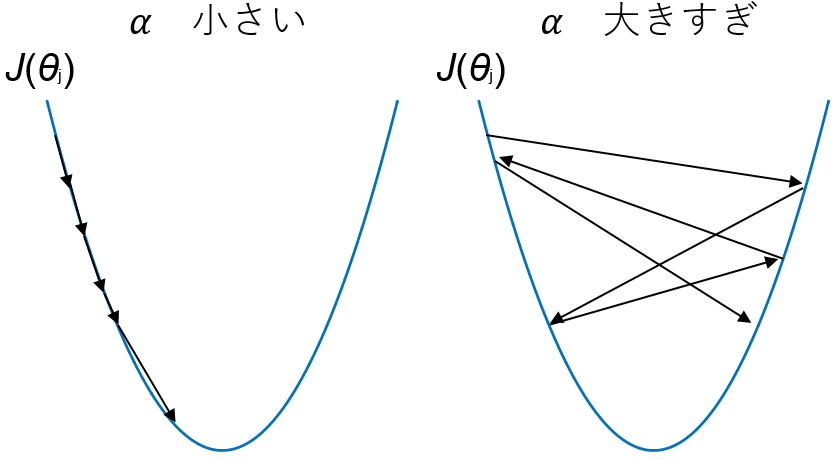
　これを、$j = 0, 1, ... , n$それぞれについて同時に、$\theta_j$の値が収束するまで (目安としては、1回のアップデートでの値の変化が$10^{-3}$より小さくなるまで）繰り返します。1回のリピートで、パラメーター$\theta_j$は、（そのときの目的関数$J(\theta)$の傾き） x （学習率$\alpha$）　だけ値が変化していきます。
　
　$\alpha$の値が大きければ、1回1回の$\theta$の値の変化が大きくなります。$\alpha$が小さければゆっくりでも確実に収束しますが、$\alpha$が大きすぎると値がとびとびになり、最急降下法を繰り返しているのに目的関数$J(\theta)$が小さくならない、ということもあり得ます。

スケーリング (feature scaling)

---

　説明変数のマトリックス$X$は、今回の例では教科の得点なので、どれも同じ範囲 (0 - 100)に収まっています。しかし、もし説明変数の範囲が互いにバラバラだったならば、スケーリング (feature scaling)をして、全ての説明変数の値の範囲を、おおよそ$ -1 \leq x_i \leq 1$にする必要があります。

x_i = \frac{x_i - mean(x)}{SD(x)}

あるいは、

x_i = \frac{x_i - mean(x)}{max(x) - min(x)}

とすれば、値の範囲をおおよそ-1から1にすることができます。$mean(x)$はベクトル$x$の平均値、$SD(x)$は$x$の標準偏差、$max(x)$、$min(x)$は、それぞれ最大値と最小値を表します。

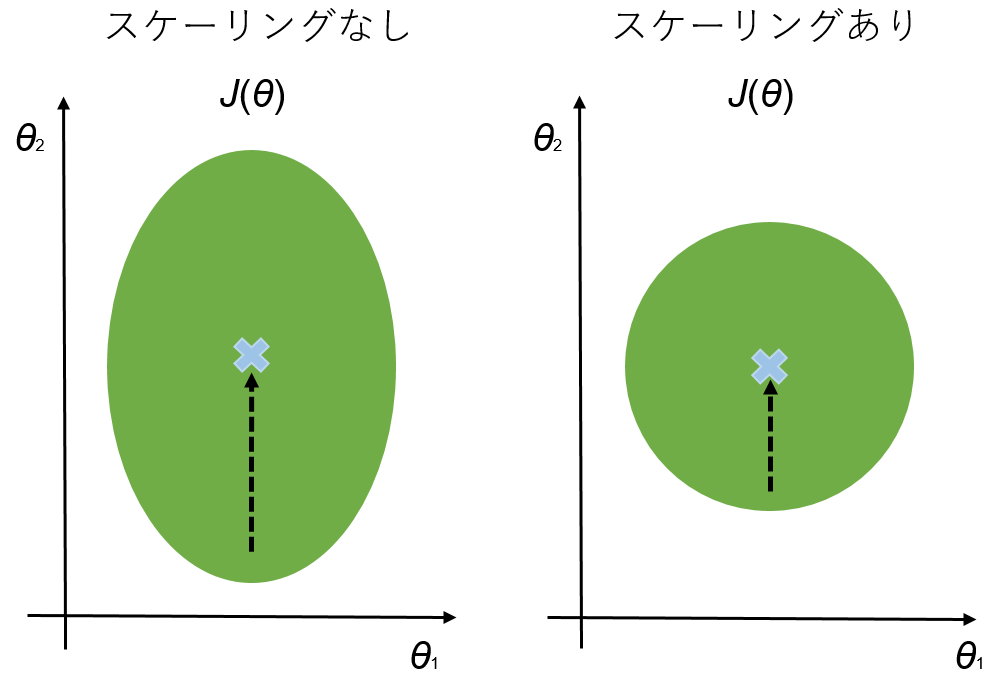
　スケーリングの利点
　$\theta$同士の範囲に差があると、目的関数$J(\theta)$が非対称的な形になり、最急降下法で最小値にたどり着くまでに時間がかかります。スケーリングによって、目的関数$J(\theta)$が対称的な形となり、最急降下法で最小値までたどり着く時間が短くなります。

正規方程式 (Normal Equation)

　最急降下法以外に、目的関数$J(\theta)$の最小値を求める方法として、正規方程式 (normal equation)を解く方法があります。

\theta = (X^{\mathrm{T}} X)^{-1} X^{\mathrm{T}} y

　これを解くと、一発で目的関数$J(\theta)$が最小となる$\theta$を求めることができます。

　正規方程式があれば最急降下法なんていらないじゃん？

　と思うのが当然だと思います。

　ただ、最急降下法 (Gradient Descent)にもメリットがあり、正規方程式 (Normal Equation)にもデメリットはあります。

最急降下法

学習率$\alpha$を選ぶ必要がある

　

たくさんの繰り返しによって解にたどり着く

　

説明変数の数が多くても (n = 1,000,000程度)上手く動く

正規方程式

学習率$\alpha$を選ばなくてよい

　

直接解が求められる

　

Xのサイズが大きい場合、計算に時間がかかる

　なので、説明変数の数が100万を超えるような場合でなければ、正規方程式を使えばよいのですね。

pinv(X'*X)*X'*y

　Matlab / Octaveであれば、上記のコマンドで正規方程式を解くことができます。

#まとめのまとめ#

• 重回帰分析とは、複数の説明変数で１つの目的変数を予測する方法である。
• 目的関数 (cost function)の最小値を求めるには、最急降下法 (gradient descent)か正規方程式 (normal equation)を使う。
• 説明変数同士の値の範囲を合わせるため、スケーリング (feature scaling)を用いる。

#終わりに#
　次回は主に、ロジスティック回帰 (logistic regression)による分類 (classification)のお話です。