機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第七弾は、みんな大好き**サポートベクターマシーン (Support Vector Machine)**です。誰もが名前を知っているアルゴリズムですが、実際のところ一体何をしているのか、ざっくり見ていきたいと思います。
過去の記事
Coursera Machine Learning (1): 機械学習とは?単回帰分析、最急降下法、目的関数
Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式
Coursera Machine Learning (3): ロジスティック回帰、正則化
Coursera Machine Learning (4): ニューラルネットワーク入門
Coursera Machine Learning (5): ニューラルネットワークとバックプロパゲーション
Coursera Machine Learning (6): 機械学習のモデル評価(交差検定、Bias & Variance、適合率 & 再現率)
サポートベクターマシーンとロジスティック回帰 (SVM & Logistic Regression)
SVMのざっくりしたイメージは、多くの人が共有していると思います。
「なんか、マージン(?)を最大化して……分類するんでしょ?」

こんな感じですね。
SVMが実際どのようにマージン (Margin)を決めているのか、ニューラルネットワークでもそうでしたが、**ロジスティック回帰 (Logistic Regression)**と比較するとわかりやすいです。
「ロジスティック回帰ってなんだっけ?」という人は、昔の記事の前半部分を見てあげてください。
ロジスティック回帰の目的関数$J(\theta)$は、以下のように書けました。
J(\theta) = -y (log \frac{1}{1 + e^{-\theta^{\mathrm{T}} x}}) - (1-y) log(1 - \frac{1}{1 + e^{-\theta^{\mathrm{T}} x}})
この目的関数を最小にするには、$z = \theta^{\mathrm{T}}x$として、
- $y = 1$のとき、$z \gg 0$
- $y = 0$のとき、$z \ll 0$
となるような$\theta$を学習する必要がありました。
SVMでは、これをよりアクロバットに解釈します。
「まどろっこしいロジスティック関数はやめる。$y = 1$のとき$z \gg 0$とかもやめる。**$y=1$のとき、$z \ge 1$ならそのときのコストを$0$にしちゃおう。同様に、$y = 0$のとき、$z \le -1$ならそのときのコストを$0$**にしちゃおう」

この大胆な目的関数$cost_{(y=1)}(z)$、$cost_{(y=0)}(z)$の設計により、SVMが最小にすべき目的関数は、**正規化パラメーター$\lambda$**を含めると以下のように書けます。
\frac{1}{m} \sum^m_{i=1} [y^{(i)} cost_1 (\theta^{\mathrm{T}} x^{(i)}) + (1 - y^{(i)}) cost_0 (\theta^{\mathrm{T}} x^{(i)})] + \frac{\lambda}{2m} \sum^n_{i=1} \theta^2_j
ちょっと変形します。両項で$m$ (データサンプル数)が重複してるので、正則化パラメーター$\lambda$も含め、**$C = \lambda/m$**とすると、
C \sum^m_{i=1} [y^{(i)} cost_1 (\theta^{\mathrm{T}} x^{(i)}) + (1 - y^{(i)}) cost_0 (\theta^{\mathrm{T}} x^{(i)})] + \frac{1}{2} \sum^n_{i=1} \theta^2_j
のように書き直すことができます。
ここで、SVMの大胆な解釈が効いてきます。
-
$y^{(i)} = 1$のとき、$\theta^{\mathrm{T}} x^{(i)} \ge 1$なら、$cost_1 = 0$
-
$y^{(i)} = 0$のとき、$\theta^{\mathrm{T}} x^{(i)} \le -1$なら、$cost_0 = 0$
なので、この条件を満たす$\theta$を取ると最初の$C$がついた項の値は0になります。
結局第二項だけが残るので、最終的に、SVMの課題は以下を最小にすることです。
\frac{1}{2} \sum^n_{i=1} \theta^2_j \\
s.t. \hspace{15pt} \theta^{\mathrm{T}}x^{(i)} \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
\hspace{30pt} \theta^{\mathrm{T}}x^{(i)} \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$s.t.$はsuch that (~となるような)の略です。だいぶ見やすくなりましたね。
決定境界 (Decision Boundary)
細かい数学的な事情は抜きにして、SVMがどうやってマージンを決めるのか簡単に見ていきます。
$\theta^{\mathrm{T}} x^{(i)}$はベクトルの内積 (Inner Product) を計算しているので、**ベクトル$x^{(i)}$のベクトル$\theta$への投射の長さを$p^{(i)}$**とすると、以下のように書き直せます。高校数学で学んだ内積の定義そのままですね。
\theta^{\mathrm{T}} x^{(i)} = p^{(i)}・|| \theta ||
このとき、$|| \theta ||$は、ベクトル$\theta$の長さを表します。

「内積は長さx長さだから、値はプラスにしかならないな!」
とうっかり思いがちですが、上図右のように、投射の着地点が投射されるベクトルの反対側にあると、値はマイナスになります。
SVMは、データ1つ1つのサンプル$x^{(i)}$に対し、
- $y^{(i)} = 1$ なら $p^{(i)}・||\theta|| \ge 1$
- $y^{(i)} = 0$ なら $p^{(i)}・||\theta|| \le -1$
となるような $\theta$ を探していきます。注意しないといけないのは、
\frac{1}{2} \sum^n_{i=1} \theta^2
が最小値を取るという条件なので、$\theta$自身はあまり大きくなれません。
そのため、投射の長さ$p^{(i)}$が大きくならないといけません。
結果として$\theta$はデータが広がる方向を貫くベクトルになり、決定境界 (Decision Boundary)は、$\theta$の始点を通り直交するベクトルになります。

カーネル (Kernel)
今までは線形分類を前提にした話でしたが、SVMもロジスティック回帰やニューラルネットワークと同様に非線形分類ができます。それを可能にするのが**カーネル (Kernel)**です。カーネルというとちょっと怖そうな感じがしますが、数学では単に「重みづけする関数」といった意味合いです。
カーネルは、元のデータ$x$を新しい説明変数 (feature) $f$に変換するための道具です。今回は、**ガウシアンカーネル (Gaussian Kernel)を使い、手持ちのデータ$x$と、$x$と同次元のとある点$l^{(1)}$ (ランドマークと呼ぶ)の類似性 (similarity)**を定量します。
f1 = similarity(x,l^{(1)}) = exp(-\frac{||x - l^{(1)}||^2}{2 \sigma^2})
新しい説明変数$f1$は、**$x$と$l^{(1)}$が近ければ$1$、遠ければ$0$**に近い値を出してくれます。
「で、これがどう非線形分類にかかわるの?」
ということですが、簡単な例で言うと、ランドマーク (Landmark)を3つ取り、$x$を新しい3つの説明変数$f1, f2, f3$にカーネルを使って変換します。すると、SVMは、
y = 1 \hspace{15pt} if \hspace{15pt} \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 \ge 0
\\
y = 0 \hspace{15pt} if \hspace{15pt} \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 < 0
というルールに基づいて予測を行います。ざっくり言うと、$f1, f2, f3$と説明変数を増やすことで、$x_1^2, x_2^2, x_1 x_2$と説明変数を増やし多項回帰 (Polynomial Regression) を行います。多項回帰ってなんだっけという人は、過去の記事の下の方を見てください。
(出典:Wikipedia -- Kernel Method)
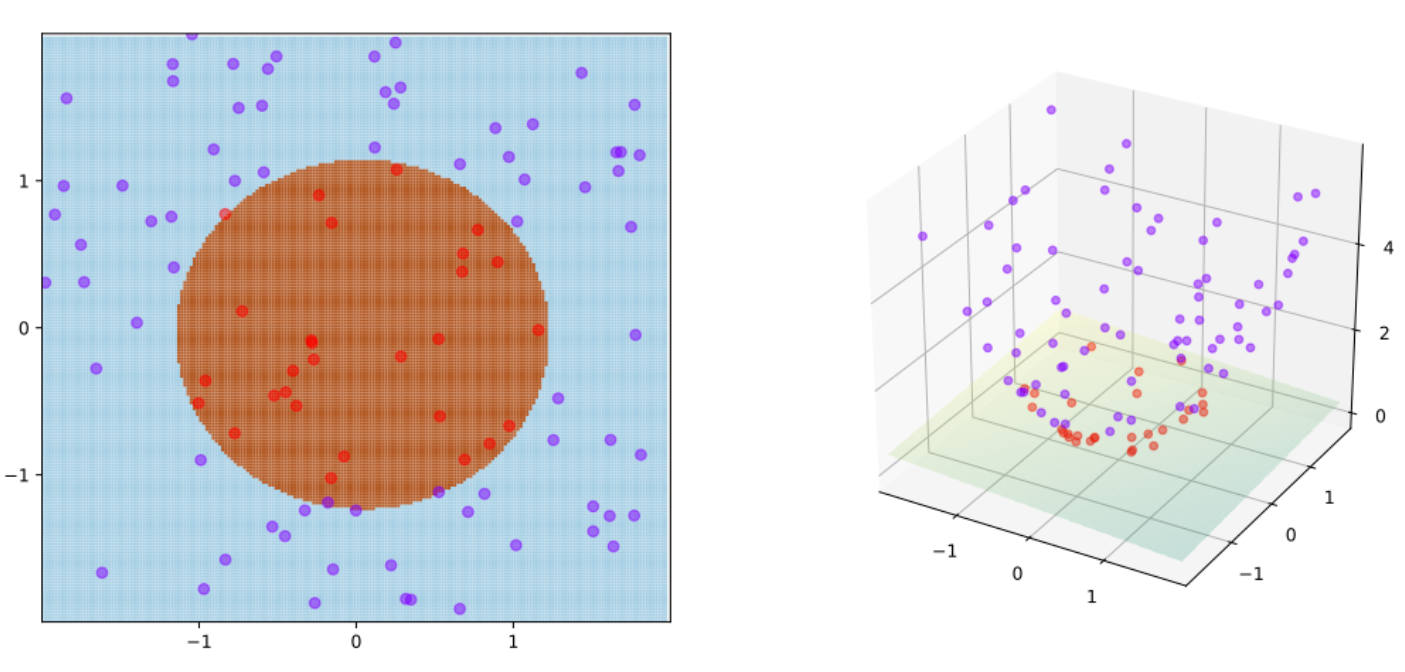
上図はウィキペディアのカーネル法のページからの引用です。左図が元データの分布です。決定境界が線形だと、赤と青のデータを分離することはできませんが、決定境界が円なら綺麗に分けることができます。そこでカーネル法を使って、
F: (x,y) \to K: (x, y, x^2 + y^2)
と、元の空間 ($F$) から新しいカーネル空間($K$、3次元)に投射します。すると、線形の決定境界で綺麗に赤と青のデータを分けることができます。
つまり元の空間では決定境界が非線形になれなくても、投射先のカーネル空間では決定境界が線形になることができ、SVMが使えるわけですね。このように、カーネル法を用いれば非線形分類もSVMを使ってできるようになります。
注意点
-
どのSVMのライブラリを使うにせよ、SVMの正規化パラメーター$C$を決めないといけません。$C$は$\lambda$の逆数なので、$C$が小さい ($\lambda$が大きい)とアンダーフィット (low variance, high bias)しやすくなり、$C$が大きい ($\lambda$が小さい)とオーバーフィット (high variance, low bias)しやすくなります。
-
ガウシアンカーネルを使う場合は、ガウシアン(正規分布)の広さを表すパラメーター$\sigma$を決める必要があります。$\sigma$が大きいと正規分布の広がりが大きくなり、類似性が検出されやすく、アンダーフィット (low variance, high bias)しやすくなります。逆に、$\sigma$が小さいと正規分布の広がりが小さくなり、類似性が検出されにくくなるため、オーバーフィット (high variance, low bias)しやすくなります。
-
ランドマーク$l$となる点の選択ですが、元のデータ$x$をそのまま使います。つまり、**$l^{(1)} = x^{(1)}, ... , l^{(m)} = x^{(m)}$**とします。結果、新しい説明変数$f$が$m$個できます。データサンプル数$m$ が大きい(例えば、$m > 10,000$)と計算量が膨大になるため、ロジスティック回帰を使うか、カーネルなし (Linear Kernel)のSVMを使った方がいいです。

まとめのまとめ#
- SVMでは、データクラス間のマージン(隙間)を最大にするように決定境界を求める。
- カーネルを使うことで、データ$x$を新しい説明変数$f1,f2,...$に変換し、非線形分類ができる。
終わりに#
今回はSVMについてでした。ニューラルネットワークと同様にロジスティック回帰の延長ではありますが、目的関数の解釈や、カーネルを使って新しく説明変数を作り出すあたりは天才的だなと思いました。みんな好きで使うわけですね。
次回は、記念すべき初・教師なし学習 (Unsupervised Learning) 回です。K-MeansとPCA (Principal Component Analysis)を扱います。