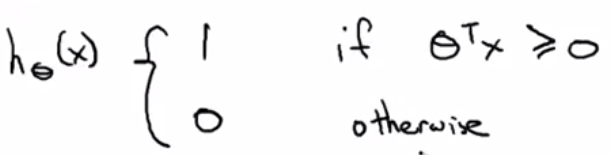Courseraの機械学習コースの7週目です。前回までに学んだロジスティック回帰、ニューラルネットワークと今回のSVMを使えるようになると、多くの問題に対応できるようになるらしいです(決定木はそんな重要でもない?)。
記事「Coursera機械学習入門オンライン講座虎の巻(文系社会人にオススメ)」を最初に読むことをお勧めします。
サマリ
実績時間:約5.5時間
目安時間:約5時間(正確には4時間54分)
※コースに各章の時間目安が書かれていて、それを足しただけです。
一覧
| No. | 章 | 目安時間 | 内容 |
|---|---|---|---|
| 1.1 | Large Margin Classification | 43分 | SVMにおけるマージンの考え方 |
| 1.2 | Kernels | 30分 | カーネル |
| 1.3 | SVMs in Practice | 21分 | SVMに関する実践的内容 |
| 1.4 | Review | 200分 | クイズとプログラム演習 |
1. Support Vector Machines
1.1. Large Margin Classification
1.1.1. Optimization Objective
Video:14分
SVMの概要です。
グラフを見るとロジスティク回帰と比べて$cost(z)$を求める関数が直線になっています(黒線がロジスティック回帰で、青線がSVM)。
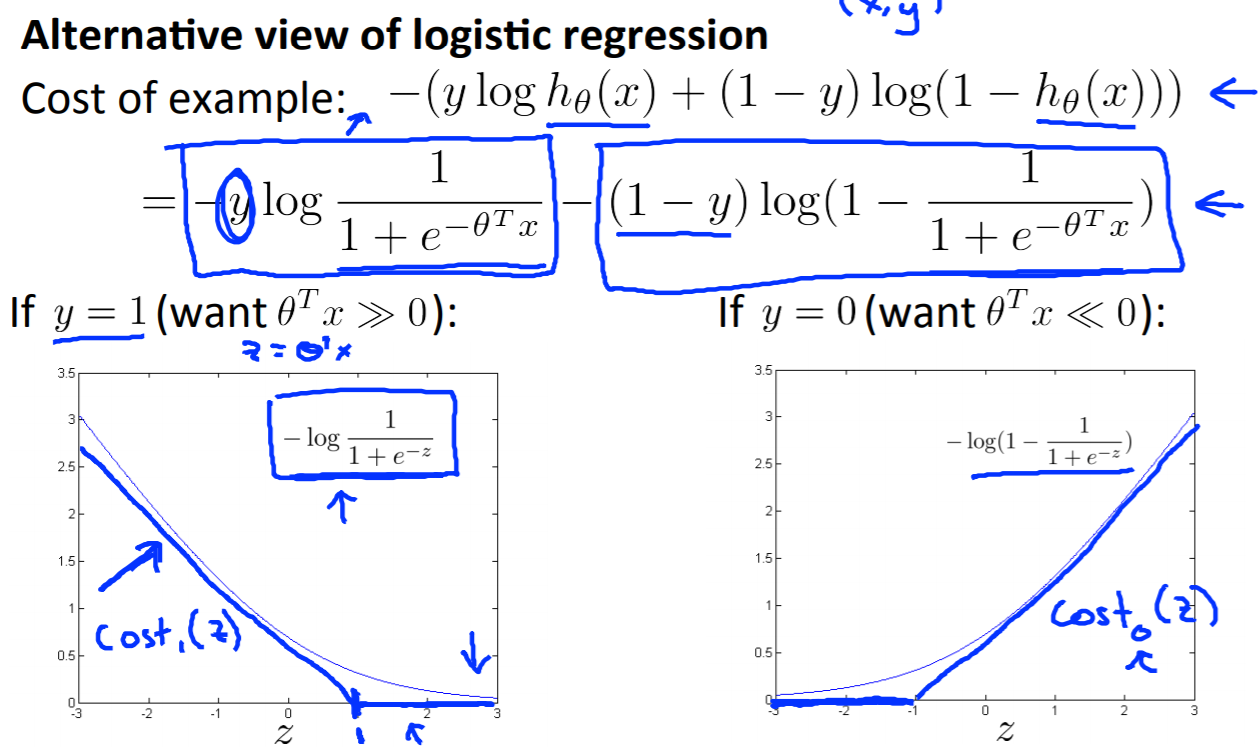
ロジスティック回帰の最適化の式は以下の通りでした。
※$Cost_1$は$y$(正解)が1の場合、$Cost_0$は$y$(正解)が0の場合の誤差を示します。
\displaystyle\mathop{\mbox{min}}_\theta\ \frac{1}{m}\left[\sum_{i=1}^{m}y^{(i)}\text{cost}_1(\theta^Tx^{(i)}) + (1-y^{(i)}) \text{cost}_0(\theta^Tx^{(i)})\right]+\frac{\lambda}{2m}\sum_{j=1}^n\theta^2_j
SVMは下記の式となります。基本的には似ています。慣習上、正則化パラメータ$\lambda$は使わないらしく代わりに$C$を1つ目の項(トレーニングセットに対するコスト関数)を乗算します。ただ、$C = \frac{1}{\lambda}$を示し、実質的に同じです。
\displaystyle\mathop{\mbox{min}}_\theta\ C\left[\sum_{i=1}^{m}y^{(i)}\text{cost}_1(\theta^Tx^{(i)}) + (1-y^{(i)}) \text{cost}_0(\theta^Tx^{(i)})\right]+\frac{1}{2}\sum_{j=1}^n\theta^2_j
1.1.2. Large Margin Intuition
Video:10分
SVMにおけるマージンの簡単な説明。
SVMでの誤差(コスト)は以下の定義で、ロジスティック回帰と異なり完全に0になる場合が多いです。
-
$y^{(i)} = 1$のとき、$\theta^{\mathrm{T}} x^{(i)} \ge 1$なら、$cost_1 = 0$
-
$y^{(i)} = 0$のとき、$\theta^{\mathrm{T}} x^{(i)} \le -1$なら、$cost_0 = 0$
もし、全データに対して正解となるのであれば、最適化の式の1つ目の項の値がゼロとなりあとは正則化の問題のみが残ります。このスパっと割り切っている部分がSVMの優れているポイントらしいです。
\frac{1}{2} \sum^n_{i=1} \theta^2_j \\
もし、以下の線形分離できる問題で、マージンという考え方がなければ複数の決定境界を引くことができ、すべての決定境界のモデルは誤差がゼロとなります。より精度の高い決定境界を引くためにマージンを導入します(詳細は次の章)。
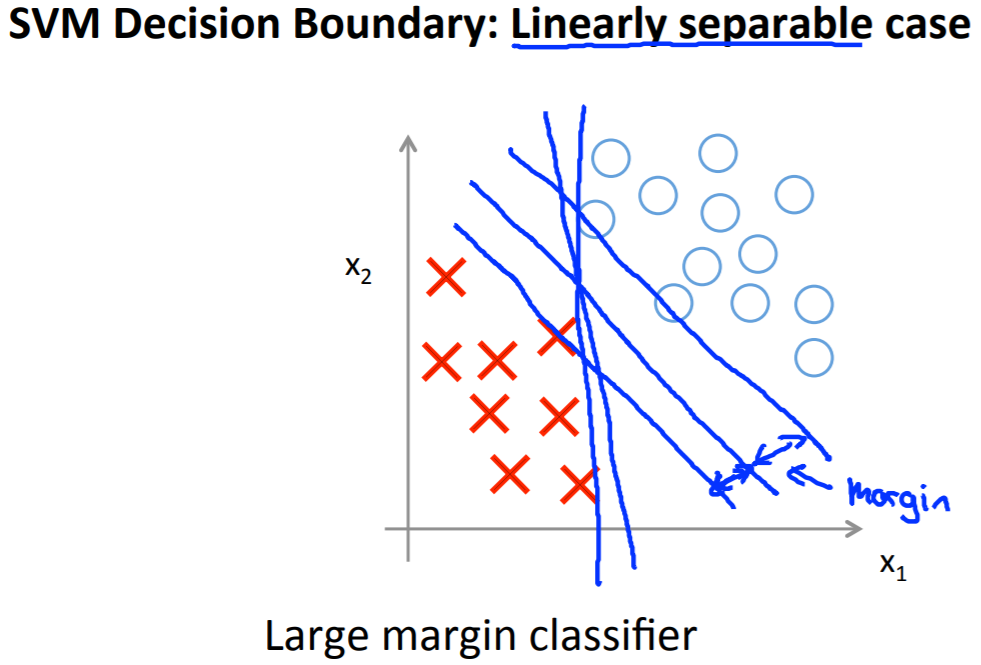
1.1.3. Mathematics Behind Large Margin Classification
Video:19分
オプショナル(任意)の内容で、マージンを最大化するための数学的なバックグラウンドについてです。非常に浅く理解しました。短時間ではしっかりと理解できませんでした。
記事「サポートベクターマシン(SVM)とは?〜基本からPython実装まで〜」などに非常にわかりやすくまとめられています。
1.2. Kernels
1.2.1. Kernels I
Video:15分
非線形の決定境界を引くための**カーネル(Kernel)**というテクニックの説明です。
線形の決定境界で分類できない場合には、多項式回帰でやったような方法で分類ができます。しかし多項式は計算コストが高く、どのような多項式が高い精度を出すかわからないという欠点があります。
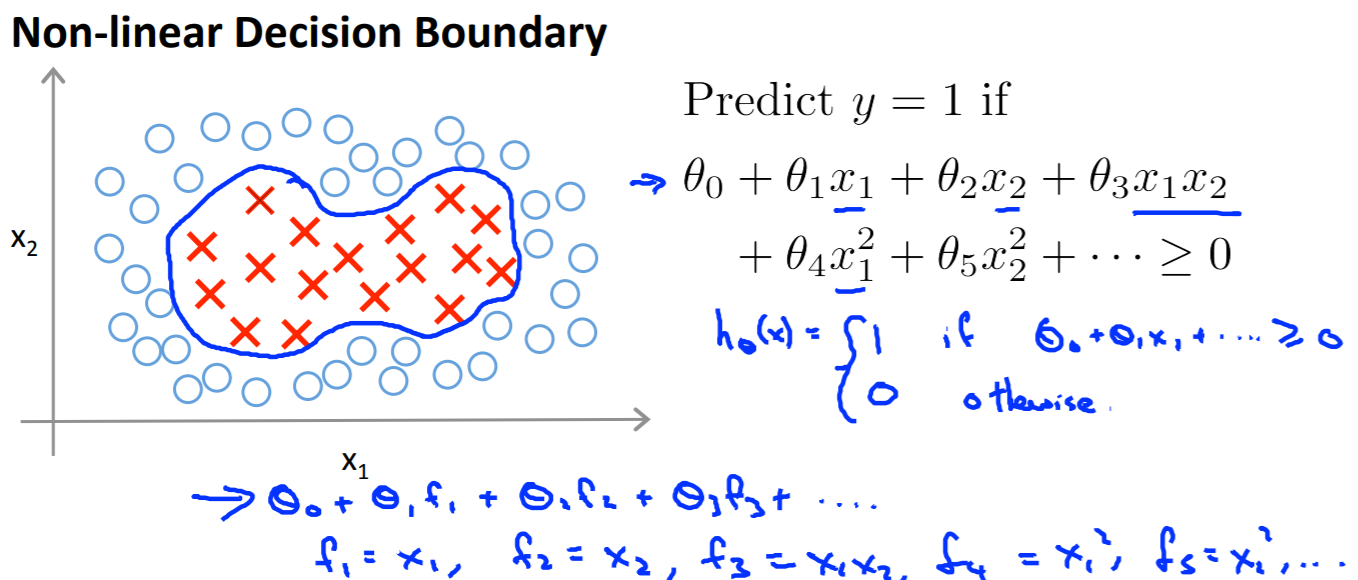
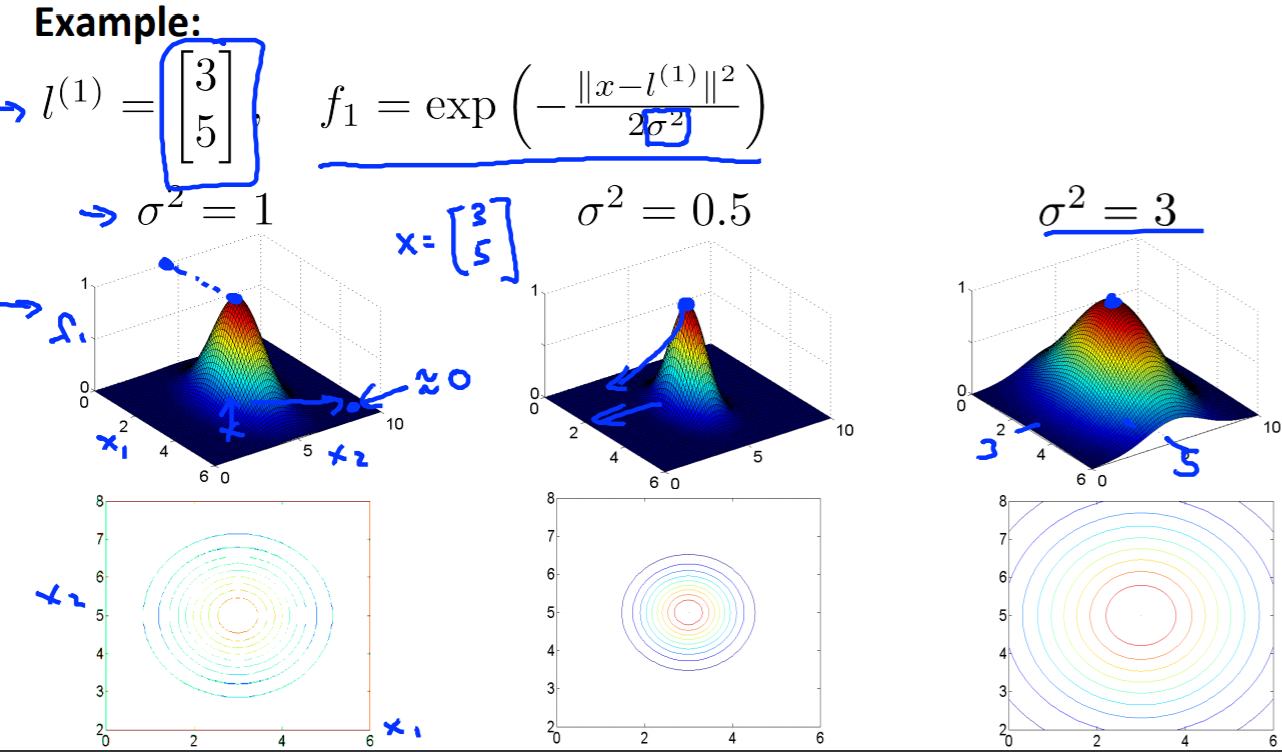
カーネル(Kernel)では、ランドマーク$l^{(i)}$を使った関数$f_i$を使います。カーネル(Kernel)にはいくつか種類があります。今回使うガウシアンカーネルは以下の式でランドマーク$l^{(i)}$からの距離の近似を求めます。
{f1 = similarity(x,l^{(1)}) = exp(-\frac{||x - l^{(1)}||^2}{2 \sigma^2})}
仮にランドマークを3つ準備すると自ずと関数$f_i$も3つ使うこととなり、以下の式で計算をします。これで説明変数が増えていきます。
{y = 1 \hspace{15pt} if \hspace{15pt} \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 \ge 0
\\
y = 0 \hspace{15pt} if \hspace{15pt} \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 < 0}
ちなみに${f1 = similarity(x,l^{(1)}) = exp(-\frac{||x - l^{(1)}||^2}{2 \sigma^2})}$に出てくる$\sigma$はガウシアンカーネルのパラメータです。パラメータ$\sigma$の値を大きくするとランドマーク$l$との関係が厳しく評価されます(距離が近くないと分類に影響を及ぼさない)。
1.2.2. Kernels II
Video:15分
ランドマークの選び方とSVMのパラメータについてです。
ガウシアンカーネルのランドマーク$l^{(m)}$は、元データ$x^{(m)}$をそのまま使用します。そしてデータ数だけ、$f_m$を計算します。

そしてSVMのパラメータ$C$と$\sigma$に関する注意点です。
$C$が大きいとLower Bias, High variance(ハイバリアンス)になりやすいです。
$\sigma$が大きいとハイバイアス、Lower varianceになりやすいです。

※SVMは難しいので自分で実装するのではなく、ライブラリの関数を使うことが推奨らしいです。確かに難しい・・・
1.3. SVMs in Practice
1.3.1. Using An SVM
Video:21分
SVMを使う際の注意点です。
- ガウシアンカーネルを使う前に2週目で学習したFeature Scalingしておく
- 特徴量の数・データ数から選択するアルゴリズムはこんな感じ
| 特徴量の数 | データ数 | アルゴリズム |
|---|---|---|
| 約1万 | 10から1000 | ロジスティック回帰/カーネルなしSVM |
| 1から1000 | 10から5万 | ガウシアンカーネルSVM |
| 1から1000 | 5万以上 | (特徴量を増やして)ロジスティック回帰/カーネルなしSVM |
- ニューラルネットワークは上記の場合に対して、だいたい良い精度が出るが、訓練スピードが遅い
- ロジスティック回帰とカーネルなしSVMはセットになっているが、アルゴリズムが似ているためほぼ同じような振る舞いをするらしい。しかし、SVMは非線形の問題に対してカーネルを使ってこそ真価を発揮する。
1.4. Review
1.4.1. Lecture Slides
Reading:10分
スライドPDF。
1.4.2. Support Vector Machines
Quiz:5問, Reading:10分
80%で一発合格。
SVMではない設問に対して間違っていました。ロジスティック回帰は局所最適解に陥ることはないらしい。記事「ロジスティック回帰のコスト関数が凸関数であることについて」に理由が書かれています。
1.4.3. Support Vector Machines
Programming Assignment:180分
SVMを使った分類のプログラム演習です。後半はスパムメール分類で、NLPも簡単に学ぶことができます。
GitHubをカンニングしたので1時間程度で終わらせました。
感想
今回の内容はベクトルの内容が基礎となっています。高校時代に勉強したベクトルについて忘れていると厳しいかもしれません。
正直、奥が深そうなので機会を見て深く勉強したいと思います。
関連記事
私より詳しくまとめてくれています。
- Coursera Machine Learning (7): サポートベクターマシーン (SVM)、カーネル (Kernel)
- カンニング用GitHub
- サポートベクターマシン(SVM)とは?〜基本からPython実装まで〜
- Coursera MachineLearning 7週目 まとめ
他の週のリンクです。
- Coursera機械学習入門コース(1週目 - 線形回帰と線形代数)
- Coursera機械学習入門コース(2週目 - 重回帰、多項式回帰、正規方程式)
- Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化)
- Coursera機械学習入門コース(4週目 - ニューラルネットワーク)
- Coursera機械学習入門コース(5週目 - ニューラルネットワークと誤差逆伝播法)
- Coursera機械学習入門コース(6週目 - 様々なアドバイス)
- Coursera機械学習入門コース(7週目 - SVM) <- 本記事
- Coursera機械学習入門コース(8週目 - 教師なし学習(K-MeansとPCA))
- Coursera機械学習入門コース(9週目 - 異常検知、レコメンデーション)
- Coursera機械学習入門コース(10週目 - ビッグデータ対応)
- Coursera機械学習入門コース(11週目 - 写真OCR)