Courseraの機械学習コースの5週目です。今回は数学的に難解な誤差逆伝播法で、理解に時間がかかります(私の理解力にも問題がありますが・・・)。
記事「Coursera機械学習入門オンライン講座虎の巻(文系社会人にオススメ)」を最初に読むことをお勧めします。
サマリ
実績時間:約6時間
目安時間:約5時間(正確には4時間47分)
※コースに各章の時間目安が書かれていて、それを足しただけです。
一覧
| No. | 章 | 目安時間 | 内容 |
|---|---|---|---|
| 1.1 | Cost Function and Backpropagation | 31分 | ニューラルネットワークのコスト関数と誤差逆伝播法 |
| 1.2 | Backpropagation in Practice | 50分 | 誤差逆伝播法の詳しい説明と実践 |
| 1.3 | Application of Neural Networks | 6分 | ニューラルネットワークを使った例(自動運転) |
| 1.4 | Review | 200分 | ニューラルネットワークと誤差逆伝播法のクイズとプログラム演習 |
1. Neural Networks: Learning
1.1. Cost Function and Backpropagation
1.1.1. Cost Function
Video:6分, Reading:4分
ニューラルネットワークのコスト関数です。
最初に変数の定義です。
| 文字 | 内容 |
|---|---|
| $L$ | ネットワークの層の総数 |
| $s_l$ | 層のニューロン数(バイアスは除く) |
| $K$ | 出力層のニューロン数 |
正則化を含んだニューラルネットワークのコスト関数です。比較のためにロジスティック回帰を2行目に記載します。
\begin{gather*} J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2\end{gather*} \\
{J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} [y^{(i)}\quad\log(h_\theta(x^{(i)}))) + (1 - y^{(i)}) \log (1 - h_\theta(x^{(i)})))] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \\
}
1.1.2. Backpropagation Algorithm
(Video:11分, Reading:10分)
誤差逆伝播法(Backpropagation)についてです。
誤差逆伝播法の計算式が複雑で、鬼門だと感じました。VideoとReadingだけでは消化不良感が残りすぎて追加で「逆伝播の仕組み」という素晴らしい記事で1.5時間ほど勉強をしました。
時間がない人は、ニューラルネットワークの後ろ(逆)から最適値を求めていく程度のレベルでもいいように思います。
計算方法
訓練データセットを$\lbrace (x^{(1)}, y^{(1)}) \cdots (x^{(m)}, y^{(m)})\rbrace$とします。
すべての$i, j, l$の値に対して $\Delta^{(l)}_{i,j} := 0$とします。
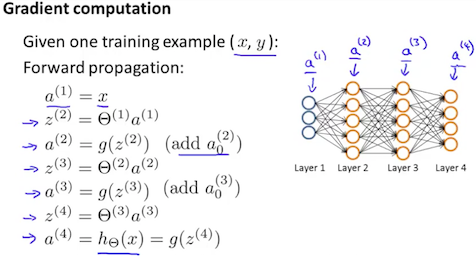
- まず、1層目のニューロンは $a^{(1)} := x{(t)}$ です。
- フォワードプロパゲーションで(前から順に) $a^{(l)}$ を $for l=2,3,…,L$のループで計算
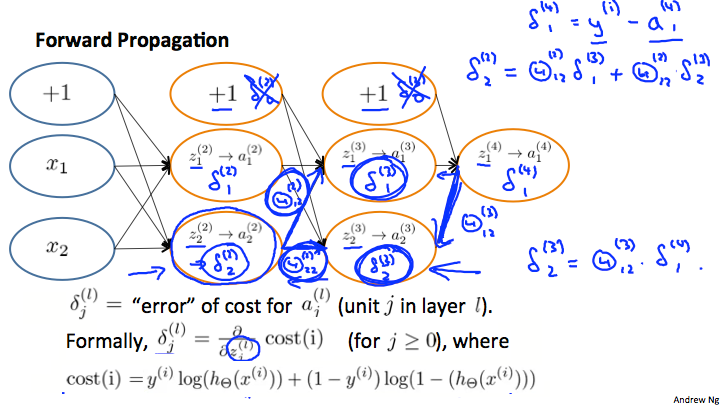
2の説明です。$a^{(j)}$は活性化関数を通した後の値で、$z^{(j)}$は活性化関数を通す前の値です。$a^{1}$は入力$x$で、$a^{L}$は出力$y$を示します。
3. $y^{(t)}$を使って$\delta^{(L)} = a^{(L)} - y{(t)}$を計算
4. 以下の計算式を使って$\delta^{(L-1)}, \delta^{(L-2)}, \delta^{(2)}$を計算
\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)})\ .*\ a^{(l)}\ .*\ (1 - a^{(l)})
5. 最後にパラメータ(上の式)とバイアス(下の式)の値を更新します。
D^{(l)}_{i,j} := \dfrac{1}{m}\left(\Delta^{(l)}_{i,j} + \lambda\Theta^{(l)}_{i,j}\right) \quad if \quad j \neq 0\\
D^{(l)}_{i,j} := \dfrac{1}{m}(\Delta^{(l)}_{i,j} \quad if \quad j = 0)
1.1.3. Backpropagation Intuition
Video:12分, Reading:4分
またまた誤差逆伝播法(Backpropagation)についてです。数学的に複雑なので例をあげて説明してくれています。
正則化ありのニューラルネットワークのコスト関数です。
\begin{gather*}J(\Theta) = - \frac{1}{m} \sum_{t=1}^m\sum_{k=1}^K \left[ y^{(t)}_k \ \log (h_\Theta (x^{(t)}))_k + (1 - y^{(t)}_k)\ \log (1 - h_\Theta(x^{(t)})_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l+1} ( \Theta_{j,i}^{(l)})^2\end{gather*}
正則化をやめて、二値分類にした場合(最終出力層が1ニューロン)は以下のようにシンプルになります。
cost(t) =y^{(t)} \ \log (h_\Theta (x^{(t)})) + (1 - y^{(t)})\ \log (1 - h_\Theta(x^{(t)}))
$\delta_j{(l)}$は、$a_j^{(l)}$の誤差です。より正確に言うとコスト関数を偏微分したデルタ値です。
\delta_j^{(l)} = \dfrac{\partial}{\partial z_j^{(l)}} cost(t)
1.2. Backpropagation in Practice
1.2.1. Implementation Note: Unrolling Parameters
Video:7分, Reading:3分
Ovtaveでのパラメータの扱い方(展開方法)についてです。ニューラルネットワークで多次元配列化したパラメータをどうやってプログラム上で扱うかの話です。

1.2.2. Gradient Checking
Video:11分, Reading:3分
誤差逆伝播法(Backpropagation)は、よくプログラムバグが潜んでいるらしく、チェックのために手法としてGradient Checkingを紹介。
計算式は以下の通り。パラメータの値に$\epsilon$(差分)を増減させて、コスト関数の差分を計算し、偏微分値をとります。
\dfrac{\partial}{\partial\Theta}J(\Theta) \approx \dfrac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2\epsilon}
より詳しく書くとこんな感じ。
\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) - J(\Theta_1, \dots, \Theta_j - \epsilon, \dots, \Theta_n)}{2\epsilon}
ただ、誤差逆伝播法(Backpropagation)に比べて圧倒的に計算が遅いのであくまでもチェックとして使います。
1.2.3. Random Initialization
Video:6分, Reading:3分
すべてのパラメータ$\theta$の初期値をゼロにするとニューラルネットワークではうまく行かないので乱数を使いましょうという話。その際に$-\epsilon$から$\epsilon$の範囲内で乱数を発生させる方法Symmetry Breakingを紹介。

1.2.4. Putting It Together
Video:13分, Reading:4分
ニューラルネットワークについてのまとめです。
以下のステップでニューラルネットワークの訓練を実行します。
- 重みをランダムに初期化
- フォワードプロパゲーションで$h_\Theta(x^{(i)})$を計算
- コスト関数を実装
- 偏微分を計算する誤差逆伝播法を実装
- Gradient checkingを使って誤差逆伝播法が機能するかを確認
- 確認後に最急降下法か他のオプティマイザを使う
1.3. Application of Neural Networks
1.3.1. Autonomous Driving
Video:6分
ニューラルネットワークを使ったアプリケーション例として自動運転を紹介。ニューラルネットワークを使った訓練の仕方と自動運転をビデオで見ることができます。
1.4. Review
1.4.1. Lecture Slides
Reading:10分
ここまでのまとめスライドPDF。
1.4.2. Neural Networks
Quiz:5問, Reading:10分
1回間違えましたが2回目で80%で合格。間違ったのはケアレスミスです。
1.4.3. Neural Network Learning
Programming Assignment:180分
ニューラルネットワークの訓練に関する演習です。MNISTのような手書き文字に対する分類問題。
難しいですが、カンニングをしたので1時間ほどで終えています。一定程度の理解にとどめています。
感想
今まで学習箇所に最も時間をかけたと思います。そのくらい私には誤差逆伝播法が理解しずらかったです。多くの人にとって鬼門になるのではないでしょうか。
関連記事
私より詳しくまとめてくれています。
他の週のリンクです。
- Coursera機械学習入門コース(1週目 - 線形回帰と線形代数)
- Coursera機械学習入門コース(2週目 - 重回帰、多項式回帰、正規方程式)
- Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化)
- Coursera機械学習入門コース(4週目 - ニューラルネットワーク)
- Coursera機械学習入門コース(5週目 - ニューラルネットワークと誤差逆伝播法) <- 本記事
- Coursera機械学習入門コース(6週目 - 様々なアドバイス)
- Coursera機械学習入門コース(7週目 - SVM)
- Coursera機械学習入門コース(8週目 - 教師なし学習(K-MeansとPCA))
- Coursera機械学習入門コース(9週目 - 異常検知、レコメンデーション)
- Coursera機械学習入門コース(10週目 - ビッグデータ対応)
- Coursera機械学習入門コース(11週目 - 写真OCR)