機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第五弾は、ニューラルネットワークの学習アルゴリズムである、バックプロパゲーション (backpropagation)です。
過去の記事
Coursera Machine Learning (1): 機械学習とは?単回帰分析、最急降下法、目的関数
Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式
Coursera Machine Learning (3): ロジスティック回帰、正則化
Coursera Machine Learning (4): ニューラルネットワーク入門
ニューラルネットワークによる複数クラスの分類 (Multi-class classification with neural network)
ロジスティック回帰では、ラベルがbinary ($0$ or $1$)ではなく、3以上あるとき(天気の分類:晴れ、曇り、雨・・・など)の分類課題を、one vs allという方法を使って解きました。ニューラルネットワークでも同様です。
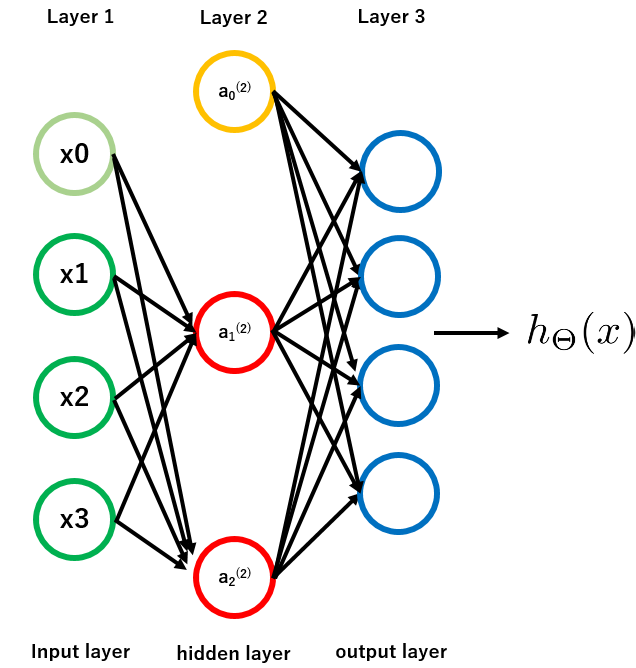
もし、天気のデータがあり、4クラス(晴れ、曇り、雨、雪)の分類課題を行うとします。このとき、$y = 0, 1, 2, 3$とラベル付けするのではなく、
y =
\begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix},
\begin{bmatrix}
0 \\
1 \\
0 \\
0 \\
\end{bmatrix},
\begin{bmatrix}
0 \\
0 \\
1 \\
0 \\
\end{bmatrix},
\begin{bmatrix}
0 \\
0 \\
0 \\
1 \\
\end{bmatrix}
と、あるクラスは$1$、それ以外は$0$とし、あくまで$0$ or $1$だけで表現します。あくまでロジスティック回帰を適用するためですね。
#ニューラルネットワークの目的関数#
目的変数$Y$に最も近づく$h_\theta (x)$を与える、インプット$X$の重み付けパラメーター$\Theta$を求めるために、目的関数 (Cost function)を導入し、最小値を計算するのは回帰分析でもニューラルネットワークでも同じです。
ロジスティック回帰における、正則化 (regularized) された目的関数は、以下のようになりました。
J(\theta) = - \frac{1}{m} [ \sum_{i=1}^m y^{(i)} log(h_\theta (x^{(i)})) + (1 - y^{(i)}) log(1 - h_\theta (x^{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^n \theta_j ^2
ニューラルネットワークの目的関数は、ロジスティック回帰の繰り返しなので、形は似ています。
J(\Theta) = - \frac{1}{m} [ \sum_{i=1}^m \sum_{k=1}^K y_k^{(i)} log(h_\Theta (x^{(i)}))_k + (1 - y_k^{(i)}) log(1 - (h_\Theta (x^{(i)}))_k)] + \frac{\lambda}{2m} \sum_{l=1}^{L - 1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l + 1} (\Theta_{j,i}^{(l)} )^2
このとき、$L$はネットワークのレイヤー数、$s_l$はレイヤー$l$のユニット数です。
目的関数$J(\Theta)$は、どんな恐ろしい形をしていても、予測値$h_\Theta (x)$と実際値$y$がどれだけずれているのか定量化したものにすぎません。
パッと見、ロジスティック回帰よりだいぶ複雑になっているように感じますが、左項はモデルを各トレーニングデータについて$K$個作る関係で$\sum_{k=1}^K$が付いているだけですし、右辺の正則化も、切片項$j = 0$ (intercept, bias unit)を除いてパラメーター$\Theta$の二乗和をとっているだけなので、やっていること自体はロジスティック回帰と何も変わりません。
この後は、目的関数$J(\Theta)$が最小になるようなパラメーター$\Theta$を計算していきます。そのためには、$J(\Theta)$の各$\Theta_{i,j}^{(l)}$偏微分である
\frac{\partial}{\partial \Theta_{i,j}^{(l)}} J(\Theta)
をどうにか計算しなければいけません。これを可能にするのが、バックプロパゲーションです。
バックプロパゲーション (Backpropagation)
まず、トレーニングデータ数が$m$個あり、説明変数$x^{(i)}$が目的変数$y^{(i)}$に対応してるとします。
次に、新しいパラメーター$\Delta_{i,j}^{(l)}$を用意します。これは、$i$番目のデータを使って計算したレイヤー$l$のアクチベーションユニット$a_j^{(l)}$における、目的関数$J(\Theta)$の偏微分が入ります。最初は$0$にしておきます。
アルゴリズムでは、$i = 1, ..., m$において、以下のステップを繰り返します。$g$はシグモイド関数。$g'$はそれを微分した関数で、$g'(z) = g(z)(1 - g(z))$です。
-
レイヤー1のアクチベーションユニット$a^{(1)}$を$x^{(i)}$設定
-
フォアワードプロパゲーション (forward propagation)で$a^{(l)} = g(z^{(l)}) = g(\Theta^{(l-1)} a^{(l-1)})$を求める ($l = 2, 3, ..., L$)
-
ネットワークのアウトプット$a^{(L)}$と、実際のラベル$y^{(i)}$との誤差$\delta^{(L)} = a^{(L)} - y^{(i)}$を計算
-
各レイヤーにおける誤差$\delta^{(l)} = (\Theta^{(l)})^{\mathrm{T}} \delta^{(l + 1)}.*g'(z^{(l)})$を計算
-
偏微分値のアップデート $\Delta_{i,j}^{(l)} := \Delta_{i,j}^{(l)} + a_j^{(l)} \delta_i^{(l+1)}$
最終的な偏微分値は、$\Delta$の平均を取って正則化したもので、以下のようになります。
D_{i,j}^{(l)} = \frac{1}{m} \Delta_{i,j}^{(l)} + \lambda \Theta_{i,j}^{(l)} \ \ \ (j \ge 1)\\
D_{i,j}^{(l)} = \frac{1}{m} \Delta_{i,j}^{(l)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (j = 0)\\
とすると、
\frac{\partial}{\partial \Theta_{i,j}^{(l)}} J(\Theta) = D_{i,j}^{(l)}
ステップ1,2で、各データ$x^{(i)}$を使ってニューラルネットワークのアウトプット$h_\Theta (x)$を求めます。これは前回と同じで、フォアワードプロパゲーション (forward propagation)と呼ばれます。
ステップ3,4,5はバックプロパゲーションで、フォアワードプロパゲーションで求めた$a^{(l)}$と$z^{(l)} = \Theta^{(l-1)} a^{(l-1)}$を使って、各レイヤーにおける誤差$\delta^{(l)}$を計算します。この誤差$\delta^{(l)}$に前のレイヤー$(l-1)$のアクチベーションユニット$a^{(l-1)}$をかけたものが、$J(\Theta)$の偏微分値になります。それを各データ$i = 1,2,...,m$で繰り返し、平均を取って正則化パラメーターを導入することで、データ$i$、レイヤー$l$の$j$番目のユニットにおける、最終的な偏微分値$D_{i,j}^{(l)}$を求めることができます。
このように、バックプロパゲーションでは、後ろのレイヤーから前のレイヤーへと計算が進んでいきます。
注意点
- 重み付けパラメーター$\Theta$の初期値は、アクチベーションユニット同士の値が同じになるのを防ぐため、ランダムな値を用います (Symmetry Breaking)。
- ネットワークの構造で迷ったときは、1つのhidden layerから始めたほうがよいです。もしhidden layerの数を複数にするなら、それらhidden layersのユニット数は全て同じであることが望ましいです。
- バックプロパゲーションにエラーがないかどうかテストする方法として、gradient checkingがあります。とても小さい値$\epsilon$ ($10^{-4}$など)を用いて**$J(\Theta)$の偏微分の近似値**$gradApprox$を計算し、それがバックプロパゲーションで求められた$D$と近い値になるか調べます。
gradApprox = \frac{J(\Theta + \epsilon) - J(\Theta - \epsilon)}{2 \epsilon} \approx D \ \ \
- gradient checking は全てのデータで繰り返すと計算がとても重くなるので、1つチェックしたらそれ以降は計算しないようにしておいたほうがよいです。
#まとめのまとめ#
- ニューラルネットワークにおける学習のアルゴリズムに、バックプロパゲーションがある。
- バックプロパゲーションでは、フォアワードプロパゲーションによって求められたパラメーターを用いて、各ユニットごとの誤差を計算することで、最終的に目的関数の偏微分値を求める。
- 重み付けパラメーターの初期値はランダムにする。
- バックプロパゲーションにエラーがないか調べるには、gradient checkingを用いる。
#終わりに#
今回はニューラルネットワークの学習というテーマで、バックプロパゲーションを扱っていました。本来の計算の方向と逆向きに計算を進めることによって、予測誤差を修正する、ということは、どうやら実際に脳の中でも起きているらしいので、面白いです。
次回は、学習アルゴリズムの評価 (evaluating a learning algorithm)についてのお話です。