Coursera機械学習入門コース(1週目 - 線形回帰と線形代数)

Courseraの機械学習コースの1週目です。機械学習の本当に基礎的な内容で簡単です。
記事「Coursera機械学習入門オンライン講座虎の巻(文系社会人にオススメ)」を最初に読むことをお勧めします。

サマリ

実績時間：約7.5時間
目安時間：約5.5時間(正確には5時間17分)
※コースに各章の時間目安が書かれています。

一覧

No.	章	目安時間	内容
1	Introduction	113分	イントロダクション
1.1	Welcome	9分	イントロダクション
1.2	Introduction	74分	機械学習の基礎とCourseraのコースの使い方
1.3	Review	30分	機械学習の基礎に関するレビュー
2	Linear Regression with One Variable	112分	一変数の線形回帰
2.1	Model and Cost Function	48分	機械学習モデルとコスト関数
2.2	Parameter Learning	44分	最急降下法での最適化
2.3	Review	20分	線形回帰のレビュー
3	Linear Algebra Review	92分	線形代数
3.1	Linear Algebra Review	72分	線形代数の基礎
3.2	Review	20分	線形代数のレビュー

講義内容

1. Instroduction

1.1. Welcome

1.1.1. Welcome to Machine Learning

Video：1分
イントロダクションです。

1.1.2. Machine Learning Honor Code

Reading:8分
コードについてコピペをせずに自分で書こう、という内容です。そのための、"Discussion Forum"に関するガイドラインが書いてあります。

1.2. Introduction

1.2.1. Welcome

Video:6分
機械学習が世の中でどんなことに使われているか。

1.2.2. What is machine learning?

Video:7分, Reading:5分
機械学習の定義。

A computer program is said to learn from experience E with respect to some task T and some performance measure P if its performance on T, as measured by P, improves with experience E.

上記のような有名な定義があるらしく、以下の3つの要素から成る。

|要素|例|
|:-:|:--|:--|
|Experienceから学ぶ|スパム判定有無のメールを観る|
|Taskを実行する|メールのスパム判定|
|計測できるPerformance|スパム判定正答率|

機械学習の分類

• 教師あり学習
• 教師なし学習
• その他(強化学習、推奨システム)

1.2.3. How to Use Discussion Forums

Reading:4分
Discussion Forumに関する注意点。禁止事項や推奨事項。

1.2.4. Supervised Learning

Video:12分, Reading:4分
Supervised Learning(教師あり学習)として**回帰(Regression)と分類(Classification)**を紹介。

1.2.5. Unsupervised Learning

Video:14分, Reading:3分
Unsupervised Learning(教師なし学習)としてクラスタリングを紹介。例としてGoogle Newsの記事グルーピングを紹介。また、カクテルパーティ効果として2人の声やバックミュージックを教師なし学習で個別に抽出することも紹介している。
最後に今回のコースでプログラミング言語にOctaveを使う理由は、学習しやすいからと話しています。

1.2.6. Who are Mentors?

Reading:3分
Mentorプログラム概要について。Discussion AreaでMentorが質問に回答してくれたりと助けてくれるようです。このMentorは、会社での一般的なメンター制度のように個人に対して1人がつくようなタイプでは無いと思います。

1.2.7. Get to Know Your Classmates

Reading:8分
「プロファイルを更新して自己紹介をみんなにしよう！」と書いていますが、やっていません。

1.2.8. Frequently Asked Questions

Reading:8分
通常のFAQです。
問題起きたら読むべく、リンクだけ。

1.3. Review

1.3.1. Lecture Slides

Reading:20分
復習用のスライドです。

1.3.2. Introduction

Quiz:5問, 10分
5問出題されました。意地悪でもない普通の問題です。
私は80%正解でした。言い訳すると結構手を抜いて答えています。英語を読むのは日本語に比べると時間かかる・・・

2. Linear Regression with One Variable

2.1. Model and Cost Function

2.1.1. Model Representation

Video:8分, Reading:3分
線形回帰モデルを例にしてモデルの式を説明しています。$h$はHypothesis(仮説)の略で$\theta$はパラメータを意味します。

h_\theta(x) = \theta_0 + \theta_1x\

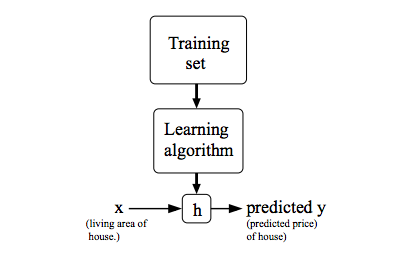
あと、訓練と推論(予測)のわかりやすい図で機械学習についての説明があります。

2.1.2. Cost Function

Video:8分, Reading:3分
線形回帰モデルを例にコスト関数を説明しています。**平均二乗誤差(Mean Squared Error)**を使っています。
平均二乗誤差は以下の数式で表され、${J}(\theta_0,\theta_1)$の値を最小化します。

{J}(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m} ({h}_\theta(x_i) - {y}_i)^2\\

2.1.3. Cost Function - Intuition I

Video:11分, Reading:4分
切片(バイアス)を0にするシンプルな線形回帰モデルの平均二乗誤差(Mean Squared Error)を詳しく説明。

h_\theta(x) = \theta_1x\\
J_(\theta_1) = \frac{1}{2m}\sum_{i=0}^{m} ({h}_\theta(x_i) - {y}_i)^2\\

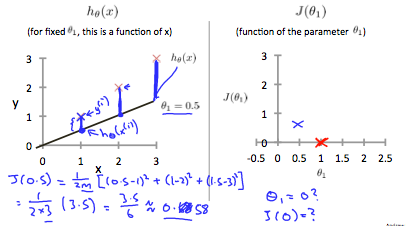
上記の線形回帰モデル$h_\theta(x)$とコスト関数$J_(\theta_1)$をグラフで説明。

2.1.4. Cost Function - Intuition II

Video:8分, Reading:3分
まず以下の前提を整理。

Hypothesis: h_\theta(x) = \theta_0 + \theta_1x\\
Parameter: \theta_0, \theta_1\\
Cost Function: J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m}({h}_\theta(x_{(i)}) - {y}_{(i)})^2\\
Goal: minimize\quad J(\theta_0,\theta_1)

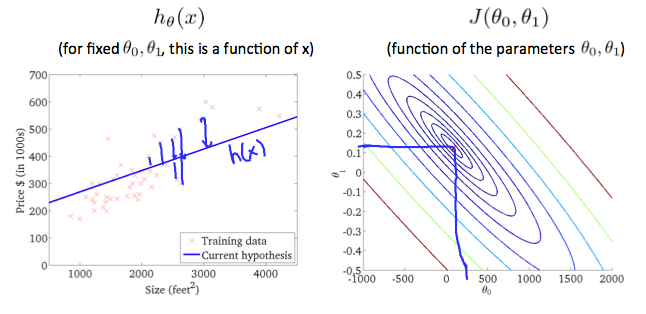
前の章と違い切片(バイアス)に値を設定し、線形回帰モデルの平均二乗誤差(Mean Squared Error)を説明。一見、わかりにくいが下図の右は等高線で平均二乗誤差の値を示しています。

2.2. Parameter Learning

2.2.1. Gradient Descent

Video:11分, Reading:3分
最急降下法(Gradient Descent)の説明です。
$J(\theta_0,\theta_1)$を最小化することが目的です。$\theta_0と\theta_1$の値をランダムに決め、それぞれの値を変更していきながら$J(\theta_0,\theta_1)$を最小化します。
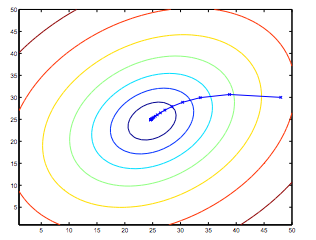
3次元のグラフでコスト関数最小化の説明。

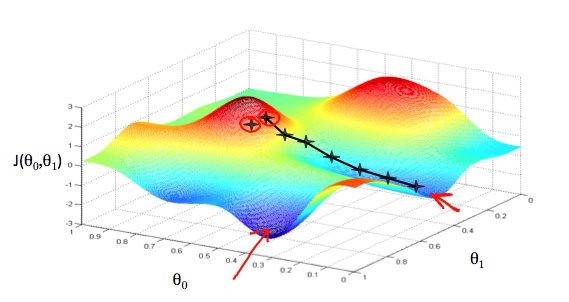
以下の計算式でパラメータを最適化していきます。

\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)

• $:=$は割当(代入)の意味。$a := a + 1$だったら、aにa+1を代入の意味。
• jの値が特徴(説明変数)のインデックス
• $\theta_0$と$\theta_1$を同時に更新する(順次更新ではない)
• $\alpha$は学習率(Learning Rate)

2.2.2. Gradient Descent Intuition

Video:11分, Reading:3分
5.1. Gradient Descentで習った最急降下法(Gradient Descent)の式をグラフで詳しく説明。

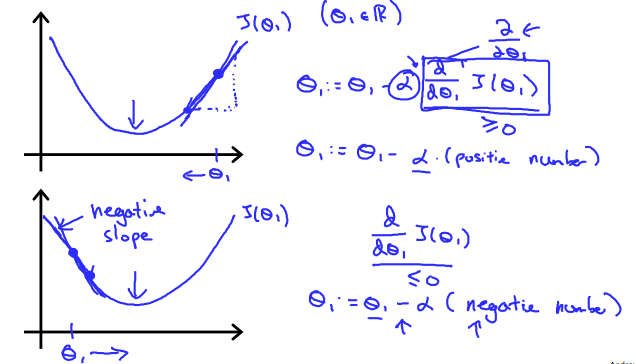
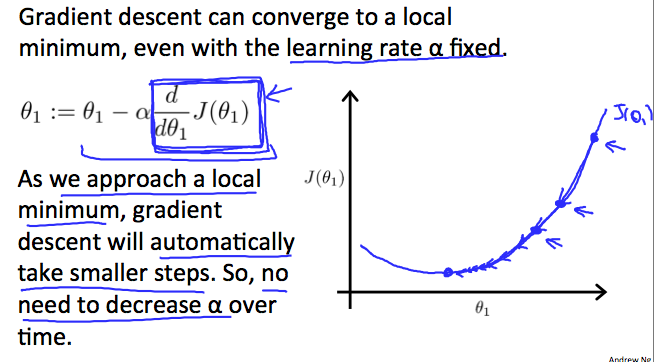
あと、学習率(Learning Rate)の意味、局所最適化についても説明。

最後に最適値に近づくと徐々にステップを小さくしていくことを説明。

2.2.3. Gradient Descent For Linear Regression

Video:10分, Reading:6分
最急降下法(Gradient Descent)を使い、線形回帰モデルの式がどのように最適化されていくかを説明。
解が収束するまで以下の式を続けます(偏微分を使っています)。

\theta_0 := \theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}({h}_\theta(x_i) - y_i)\\
\theta_1 := \theta_1-\alpha\frac{1}{m}\sum_{i=1}^{m}(({h}_\theta(x_i) - y_i)x_{i})\\

収束していく様子を図で説明してくれています。

2.3. Review

2.3.1. Lecture Slides

Reading:20分
スライドPDF。

2.3.2. Linear Regression with One Variable(Quiz:5問, 10分

またまた80%。時間かけて解けば100%いくんだろうか。5分くらいで終わらしています。

3. Linear Algebra Review

3.1. Linear Algebra Review

Linear Algebraは線形代数のことです。

3.1.1. Matrices and Vectors

Video:8分, Reading:2分
行列についてです。
こんな行列は「3×2行列」と呼びます(縦・横の順で英語では"3 by 2 matrix"と言っていました)。

A =  \left(
    \begin{array}{ccc}
      a & b  \\
      d & e  \\
      g & h 
    \end{array}
  \right)

$\mathbb{R}^{4\times2}$と表記するようです。
そして$A_{11}=a, A_{12}=b, A_{21}=D$のように行列内の値を表現。

ベクトルについても説明。
下記のベクトルは3次元ベクトルで、$\mathbb{R}^3$と表記。

y =  \left(
    \begin{array}{ccc}
      11  \\
      22  \\
      33 
    \end{array}
  \right)

慣習として行列の変数は大文字表記で、ベクトルやスカラーの変数は小文字表記らしいです。

3.1.2. Addition and Scalar Multiplication

Video:6分, Reading:3分
行列同士の足し算、行列とスカラーの乗算・割り算。

3.1.3. Matrix Vector Multiplication

Video:13分, Reading:2分
行列とスカラーの乗算と、機械学習でそれをどう使うか。

3.1.4. Matrix Matrix Multiplication

Video:11分, Reading:2分
行列同士の乗算と、線形回帰モデルで使う例。

3.1.5. Matrix Multiplication Properties

Video:9分, Reading:2分
行列同士の乗算は交換法則(Communitive)が成り立たない。$A\cdot B \neq B\cdot A$
行列同士の乗算は結合法則(Associative)が成り立つ。$A\cdot(B\cdot C) = (A\cdot B)\cdot C$
下のような単位行列(Identity Matrix)。$I$や$I_{n\times n}$で表す。$I\cdot A = A\cdot I = A$

 \left(
    \begin{array}{ccc}
      1 & 0\\
      0 & 1
    \end{array}
  \right)
 \left(
    \begin{array}{ccc}
      1 & 0 & 0  \\
      0 & 1 & 0  \\
      0 & 0 & 1 
    \end{array}
  \right)

3.1.6. Inverse and Transpose

Video:11分, Reading:3分
逆(Inverse)行列は$A^{-1}$で表す。
転置(Transpose)は行と列の入れ替え。行列$A$の転置は$A^T$と表す。

A= \left(
    \begin{array}{ccc}
      1 & 4  \\
      2 & 5  \\
      3 & 6 
    \end{array}
  \right)
\quad,\quad A^T= \left(
    \begin{array}{ccc}
      1 & 2 & 3  \\
      4 & 5 & 6
    \end{array}
  \right)

3.2. Review

3.2.1. Lecture Slides

Reading:10分
線形代数のスライドPDF。

3.2.2. Linear Algebra

Quiz:5問, 10分
またもや80%。難しくはないのですが・・・

感想

一度、忙しくて挫折して二度目のチャレンジでした。二度目だというのに約7時間と結構時間がかかりました。ただ、この7時間にはブログを書く時間を含んでいます。ただやるだけならもっと短いと思いますが、ブログに書くことは、私にとってノートに書くことと同じ意味があるのでやめられないです。数式の書き方を調べるのが、ノートをとることと比べると時間がかかってしまっている点です。7時間だと、体調悪かったり仕事が忙しかったりすると時間確保できなそうであと10週程度続けられるか非常に不安です。
内容は忘れていたことも多く、思い出せてよかったです。
英語は非常に聞き取りやすく、字幕もつければそんなに言語的不自由は感じません。だいたい1.25倍で聞いています。ただ、数学用語は慣れないので何回かは、動画を止めて英単語を調べました。

関連記事

私より詳しくまとめてくれています。

• 【機械学習】Stanford University Machine Learning / Week1【学習メモ】
• Coursera Machine Learning (1): 機械学習とは？単回帰分析、最急降下法、目的関数
• カンニング用GitHub

他の週のリンクです。

• Coursera機械学習入門コース(1週目 - 線形回帰と線形代数)<- 本記事
• Coursera機械学習入門コース(2週目 - 重回帰、多項式回帰、正規方程式)
• Coursera機械学習入門コース(3週目 - ロジスティック回帰、正則化)
• Coursera機械学習入門コース(4週目 - ニューラルネットワーク)
• Coursera機械学習入門コース(5週目 - ニューラルネットワークと誤差逆伝播法)
• Coursera機械学習入門コース(6週目 - 様々なアドバイス)
• Coursera機械学習入門コース(7週目 - SVM)
• Coursera機械学習入門コース(8週目 - 教師なし学習(K-MeansとPCA))
• Coursera機械学習入門コース(9週目 - 異常検知、レコメンデーション)
• Coursera機械学習入門コース(10週目 - ビッグデータ対応)
• [Coursera機械学習入門コース(11週目 - 写真OCR)] (https://qiita.com/FukuharaYohei/items/46c60cf591223915e6b4)