CourseraのMachine Learningでロジスティック回帰を勉強していたのですが、ロジスティック回帰のコスト関数が凸関数であることについて興味があったので調べてみました。
まずは結論から
- ロジスティック回帰のコスト関数は凸関数である。線形回帰の最小二乗法のようにコスト関数を定義した場合は凸関数とはならないが、最小二乗法とは別にコスト関数を定義することで凸関数にすることができる。
- ロジスティック回帰のコスト関数は凸関数なので、局所解=最適解となることが保証される。凸関数である前提を守る限り、ロジスティック回帰で局所解にハマったから…という議論は成り立たない(局所解があるなら前提が守られていないか、なにか別の原因がある)。
最小二乗法のようなコスト関数を定義すると凸関数にはならないというのは確かですが、そこを飛躍してロジスティック回帰=凸関数とならないというのは嘘ですので注意したいところです。Courseraの講義を見るとここはしっかり説明していますが、ネットの記事を読んでいるとたまに誤解を招きかねないのがあります。
凸関数の前提は後述の証明を見ていくときに確認していきます。
凸関数とは?凸関数のメリットとは
凸関数の定義
任意の$x,y$および$0\leq\lambda\leq1$を満たす任意の実数$\lambda$に対して不等式
$$\lambda f(x)+(1-\lambda)f(y)\geq f(\lambda x+(1-\lambda)y)\tag{1} $$
が成り立つような関数$f$を凸関数と呼びます(定義)。
凸関数のメリット
凸関数には最適化問題を解く際に非常に有用な性質があって、
定理1:凸関数の局所最適値(極小値)は大域的にも最適(最小)である
証明は以下の資料を参考にしてください。凸関数の定義や定理は以下の資料を参考にしたものです。
つまり、簡単に言うと最急降下法のように、ある初期値からずっと極小値をめがけて探索していけば、(もちろんアルゴリズムが発散せずに極小値を見つけられればですが)、結果的に最小値にたどり着くのを保証してくれるのが凸関数なのです。局所的にいいものが選ばれたが、それが本当に最良のものであるかわからないような状況で「それは最良のものだ」と保証してくれるのは、とてもありがたいことです。
凸関数をグラフで理解する
拙作の『確率的勾配降下法のメリットについて』の例と重複しますが、
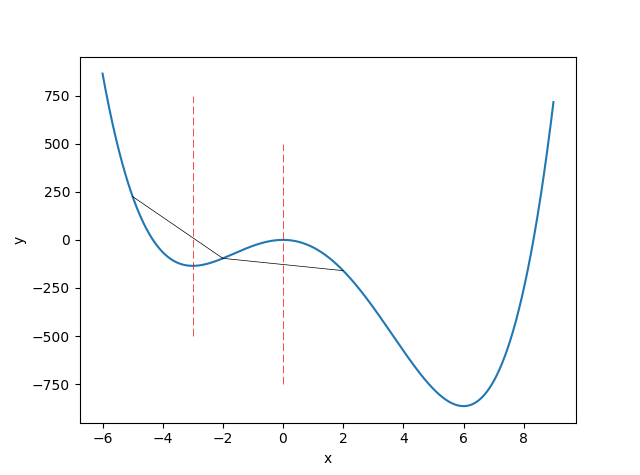
$$y=x^4-4x^3-36x^2 \tag{2}$$
という4次関数で、$-5\leq x\leq-2$において凸関数ですが、$-2\leq x\leq2$では凸関数ではありません。したがって、x全体で見るとこの(2)の4次関数は凸関数ではありません。
グラフで言うと、グラフ上のある2点を直線で引いたときに、常にグラフがその直線より下にあるのが凸関数です。
凸関数どうしの非負の和も凸関数
ロジスティック回帰のコスト関数が凸関数であることに行く前に、証明に使う重要な定理(性質)を紹介します。
定理2:$f(x), g(x)$が凸関数のときに、$\alpha, \beta\geq 0$である$h(x)=\alpha f(x)+\beta g(x)$も凸関数である
証明は(1)の凸関数の定義から、
\begin{align}
\alpha(\lambda f(x)+(1-\lambda)f(y)) &\geq \alpha f(\lambda x+(1-\lambda)y) \\
\beta(\lambda g(x)+(1-\lambda)g(y)) &\geq \beta g(\lambda x+(1-\lambda)y)\qquad(\because\alpha,\beta\geq0)\tag{3}
\end{align}
$h(x)$が凸関数であることを示すために不等式の左辺を展開します。
\begin{align}
& \lambda h(x)+(1-\lambda)h(y) \\
&= \lambda(\alpha f(x)+\beta g(x))+(1-\lambda)(\alpha f(y)+\beta g(y)) \\
&= \alpha(\lambda f(x)+(1-\lambda)f(y)) + \beta(\lambda g(x)+(1-\lambda)g(y))\tag{4}
\end{align}
右辺は、
$$ h(\lambda x+(1-\lambda)y) = \alpha f(\lambda x+(1-\lambda)y) + \beta g(\lambda x+(1-\lambda)y)\tag{5}$$
(3)の2式を足し合わせると、左辺が(4)、右辺が(5)となりますので、
$$\lambda h(x)+(1-\lambda)h(y)\geq h(\lambda x+(1-\lambda)y)\tag{6} $$
よって$h(x)$は凸関数。証明終。
ただし、α、βが負ではないことに注意しましょう。もし負の場合は、例えば$f(x)=g(x)=x^2$, $\alpha=1, \beta=-2$とすると$h(x)=-x^2$となり、$f(x), g(x)$が凸関数であったのにも関わらず、$h(x)$が凹関数になります。
「凸関数と凸関数を足したそりゃ凸関数でしょ?」当たり前のように見えますが、この素朴な性質はロジスティック回帰のコスト関数でも上手く使われています。
ロジスティック回帰のコスト関数は凸関数
最小二乗法で定義すると凸関数ではない
線形回帰では、最小二乗法のコスト関数を次のように定義しました。
\begin{align}
J(\theta) &= \frac{1}{m} \sum_{i=i}^m \frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2 \\
h_\theta(x) &= \theta^Tx\tag{7}
\end{align}
これは凸関数になります。詳細は拙作の『確率的勾配降下法のメリットについて』で書いたのでそちらを参照してください。
ロジスティック回帰では推定値の範囲を[-∞, ∞]→[0, 1]に変換するために次のように$h_\theta(x)$を定義します。
$$h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\tag{8}$$
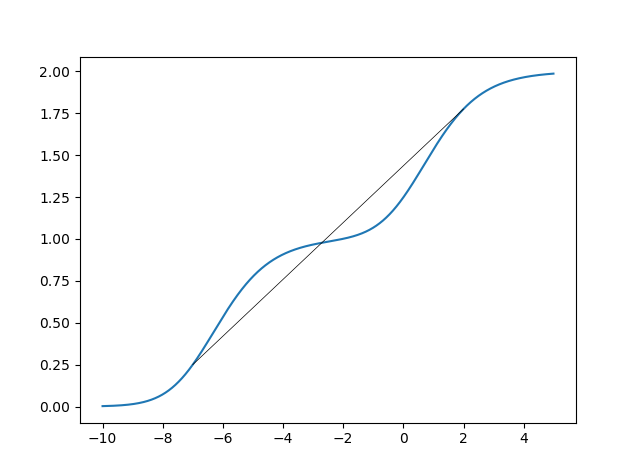
ところが今度は$J(\theta)$は凸関数になりません。わかりやすいように、
$$f(x) = \biggl(\frac{1}{1+e^{-x}}\biggr)^2+\biggl(\frac{1}{1+e^{-(x+7)}}\biggr)^2$$
としてグラフを書くと次のようになります(Σの中身を展開するとこのようになることもあり得ます)。
これは明らかに凸関数ではありません。x=[-7,2]で直線を引いてみましたが、-3付近以下ではグラフは直線の上にある一方で、それ以上ではグラフは直線の下にあるからです。式(2)の4次関数の例を思い出しましょう。
つまり、実際に使っているロジスティック回帰のコスト関数は、コスト関数が凸関数になるよう特別な形に書き換えたものなのです。
凸関数となるコスト関数
コスト関数が凸関数になるように定義したものがこちらです。普通はこちらを使います。
$$J(\theta) = -\frac{1}{m}\sum_{i=1}^m\bigl[y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\bigr] \tag{9}$$
ちなみに$y^{(i)}=0,1$です。ロジスティック回帰で推定したいことはそれが起こったか起こらないか、True/Falseのことなので。
証明
こちらに詳しい証明があります1。以下の解説はこのページを端折って説明したものです。
参考:Why is the error function minimized in logistic regression convex?
http://mathgotchas.blogspot.jp/2011/10/why-is-error-function-minimized-in.html
(9)式に注目すると、Σを展開すると実は$J(\theta)$が2種類のlogの線形和であることがわかります。つまり、
\begin{align}
-\log (h_\theta(x^{(i)})) \\
-\log(1-h_\theta(x^{(i)}))\tag{10}
\end{align}
この2式が凸関数であれば、$y^{(i)}, 1-y^{(i)}\geq0$だから定理2より、これらの非負の和である$J(\theta)$も凸関数ということになります。これがこの証明のポイントです。
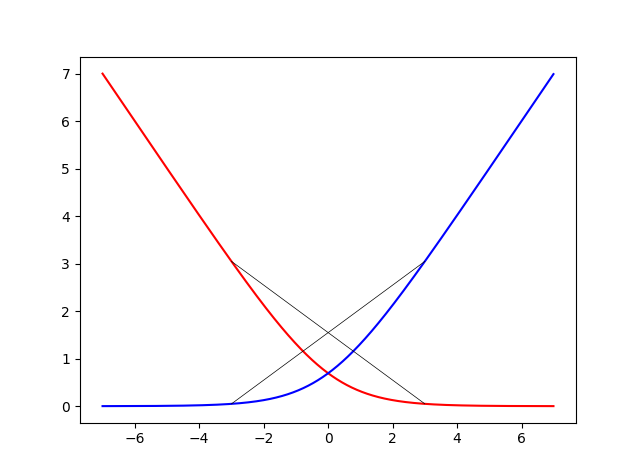
実際にこの2つの関数は凸関数です(証明は上の記事読んでください)。グラフを書いてみました。
赤が(10)式の上、青が(10)式の下です。それぞれx=[-3,3]で直線を引いてみましたが、確かに凸関数っぽい。グラフだけ見ると、x=0の近傍ではそれぞれ丸まっていますが、
\begin{align}
-\log (h_\theta(x^{(i)}))\to \min(x^{(i)}, 0) \\
-\log(1-h_\theta(x^{(i)}))\to \max(x^{(i)}, 0) \tag{11}
\end{align}
に近い形になっています。確かにこれなら凸関数というのも納得。
正則化しても凸関数
正則化した場合に凸関数ではなくなるかも?と心配かもしれせんが特に問題はありません。正則化する場合のコスト関数は、
$$J(\theta) = -\frac{1}{m}\sum_{i=1}^m\bigl[y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\bigr]+\frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 \tag{12}$$
ですが、$\theta_j^2$も凸関数なので、定理2から同様に凸関数となります。正則化の定数が負ではないことが注意がいるぐらいでしょうか。
凸関数となる条件について
定理2より、**凸関数どうしの和が凸関数となるとき、係数は0以上でなければいけないので、$0\leq y^{(i)}\leq1$を満たさなければいけません。**これがロジスティック回帰のコスト関数が凸関数となる条件です。正則化する場合は正則化の定数も0以上でなければいけません。
なので、データでy=2とか与えると急に凸関数ではなくなります。凸関数でなくなったとき、極小値=最小値となる保証はありません。ロジスティック回帰のデータのyは0か1、当たり前のようですが、証明を振り返ったときにこの条件が極めて重要だということに気付かされました。
-
クソ真面目に偏微分してヘッセ行列計算したら計算用紙8枚ぐらい使ってなにやってるんだかわからなくなって、「logistic regression convex function proof」でググったらこのページがとても鮮やかな証明していてびっくりしました。 ↩