機械学習初心者です。機械学習やディープラーニングでは、「確率的勾配降下法」というアルゴリズムがよく出てきますが、そのメリットがいまいちピンとこなかったので考えてみました。素人のポエムなのでトンチンカンなこと書いていると思います(そこそこ長いよ!)。
二次関数の最小値
全てはここから始まります。今回の確率的勾配降下法も、それのもととなった最急降下法も全てこれの応用です。
例:$ y=x^2-4x$ の最小値とそのときの$x$を求めなさい
数学的解法(1)~平方完成~
高校数学でおなじみ(?)の平方完成をします。
$$y = (x^2-4x+4)-4 = (x-2)^2-4 $$
したがって、x=2のときに最小値-4です。簡単ですね。
しかし、次数や次元が増えていくと簡単に平方完成できなくなります。もう少し一般的に使える方法を考えます。
数学的解法(2)~微分して=0となる点を求める~
**微分はグラフの接線の傾き(勾配)で、最小値となる点では必ず接線は真横になる(微分係数が0になる)**という性質を使います。この性質は確率的勾配降下法までずっとベースになるのでぜひ覚えてください。
\begin{align}
y'=\frac{\partial y}{\partial x} = 2x-4 &=0 \\
x &=2
\end{align}
結果は(1)の場合と同じです。1変数の微分はギリシャ文字のではなくて、英数のdを使うことがほとんどですが(∂と書いた場合は偏微分を表します)、1変数の偏微分は微分と同じなのであえて∂で書きます。
グラフにするとわかりやすいですね。x=2では接線は真横(微分=0)となります。
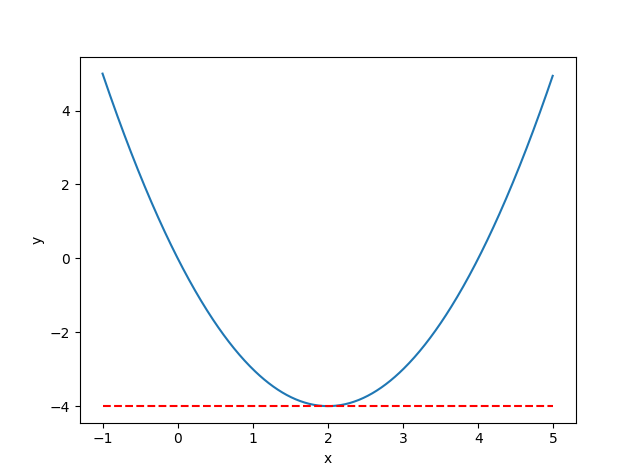
ただし、最小値→微分=0は成り立ちますが、微分=0→最小値は成り立ちません。これは少し補足します。
微分=0は必ずしも最小値とならない
\begin{align}
y'=4x^3-12x^2-72x &= 0 \\
x(x^2-3x-18) &= 0 \\
(x+3)x(x-6) &= 0 \\
x &= -3, 0, 6
\end{align}
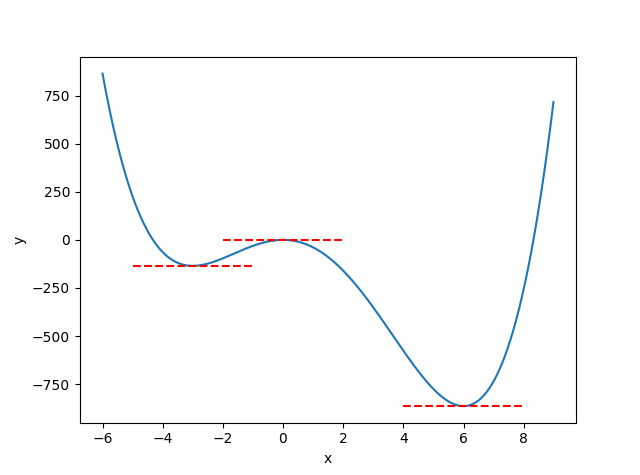
実際微分して=0と解くと、$x=-3, 0, 6$のときに最小値を取る可能性があります。グラフを見ると、global minimumという意味での最小値はx=6のときだけで、x=-3のときはlocal minimumつまり極小値でしかありません。x=0は極大値です。
機械学習でなにかの関数を最小化するときに、本当にほしいのはこの例でいうx=6のような値です。よく「局所解に陥る」という言い回しを見るのですが、概念的にはx=-3のような値が最小値として求められたということだと思います。
※専門的には、x=-3の場合を局所的最適(local optimal)、x=6の場合は大域的最適(global optimal)と言うそうです。以下の講義資料がわかりやすいです。
最急降下法(直線探索)
これまで数学的(理論的と言ったほうが正しいかも)解法で最小値を求めましたが、ディープラーニングのように何十、何百次元の関数をいくつもネットワーク上につなぎ合わせた目的関数を最小化する場合、もはや目的関数がどんなグラフをしているかもよくわからなく、平方完成のように理論的に解くことはほぼ不可能です。そこで数値計算の出番です。
荒っぽい言い方ですが、理論的な解法が神様の手法だとするなら、アルゴリズムで数値計算をしていくのは人間的な手法です。神様はその全貌を知っていたとしても、人間が容易に観測することができるのはほんのその一部の量です。その一部として、**微分(勾配)**があります。例えばですが、雨の強さ(1時間に何ミリ降ったか)というのはアメダスを見ればすぐわかっても、1ヶ月間の累積雨量を時間を変数とした関数、つまり時間でどういう推移で累積雨量が変化していていったかを見たいというのはすぐわからないですよね。雨の場合はただ足し合わせるだけなので、今回の最小化とはちょっと違うかもしれませんが、いずれにしても木を見て森を見ずならぬ、木を見て森を推測すると言うべきでしょうか。森の全貌を知っているのは神様ぐらいなので。
理論
若干脱線してしまいましたが、機械学習ではない普通の最適化問題での最急降下法について。以下の資料にとても詳しく載っているのでさらっと。例も同じです。
例:$f(x,y)=x^2-2x+4y^2$の最小値を最急降下法で求めなさい
勾配ベクトルは、
$$\nabla f(x,y) = \biggl(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\biggr)=(2x-2, 8y) $$
- $(x_0,y_0)=(0,1)$からスタート(初期値を適当に設定)
- $\nabla f(0,1)=(-2,8)$
- $f[(x_0,y_0)-\alpha\nabla f(x_0,y_0)]=f(0+2\alpha,1-8\alpha)$を最小にするステップ$\alpha$を選ぶと、$\alpha=0.13$
- 次の点は$(x_1,y_1)=(x_0,y_0)-\alpha\nabla f(x_0,y_0)=(0.26, -0.04)$
- 1に戻る…を繰り返すと最小値の点$(x,y)=(1,0)$に収束する
コード
Pythonで書くと次の通り。
import numpy as np
def steepest_descent(w0):
# w0 : 初期値のベクトル
w_before = w0
i = 1
while True:
# 勾配ベクトル
grad = w_before * np.array([2,8]) + np.array([-2,0])
# ステップ
alpha = (w_before[0]*grad[0]-grad[0]+4*w_before[1]*grad[1])/(grad[0]**2+4*grad[1]**2)
# 次の点へ
w_after = w_before - alpha * grad
# 収束したら終了
if (np.abs(w_after-w_before)<1e-6).all():
print("探索終了", np.round(w_before,6))
return w_before
# 繰り返し
print(i, w_before, "->", w_after)
i += 1
w_before = w_after
steepest_descent(np.array([0,1]))
1 [0 1] -> [ 0.26153846 -0.04615385]
2 [ 0.26153846 -0.04615385] -> [ 0.88923077 0.11076923]
3 [ 0.88923077 0.11076923] -> [ 0.91820118 -0.00511243]
4 [ 0.91820118 -0.00511243] -> [ 0.98773018 0.01226982]
5 [ 0.98773018 0.01226982] -> [ 9.90939208e-01 -5.66299499e-04]
6 [ 9.90939208e-01 -5.66299499e-04] -> [ 0.99864088 0.00135912]
7 [ 0.99864088 0.00135912] -> [ 9.98996343e-01 -6.27285599e-05]
8 [ 9.98996343e-01 -6.27285599e-05] -> [ 9.99849451e-01 1.50548544e-04]
9 [ 9.99849451e-01 1.50548544e-04] -> [ 9.99888826e-01 -6.94839433e-06]
10 [ 9.99888826e-01 -6.94839433e-06] -> [ 9.99983324e-01 1.66761464e-05]
11 [ 9.99983324e-01 1.66761464e-05] -> [ 9.99987685e-01 -7.69668295e-07]
12 [ 9.99987685e-01 -7.69668295e-07] -> [ 9.99998153e-01 1.84720391e-06]
13 [ 9.99998153e-01 1.84720391e-06] -> [ 9.99998636e-01 -8.52555650e-08]
14 [ 9.99998636e-01 -8.52555650e-08] -> [ 9.99999795e-01 2.04613356e-07]
探索終了 [ 1. 0.]
問題点
ただしこれにはいくつか問題点があります。
- この例の場合、唯一の極小値が大域的な最適解となったが、極小値が複数ある場合は収束結果が初期値に依存する
- 次のステップの計算そのものが、fについて最小化しているのと同然なので、目的関数の最小化を理論的に解けないと(微分=0とおいて数式で解けないと)最適なステップを計算することができない
- 機械学習の場合、fの最小化を数式で解けないからこういう計算をしているのであって、ステップ(学習率)をアドホックに導入してあげないといけない。そのため、初期値だけでなくステップの設定が大きく収束結果に影響を与える(最悪発散して収束しない)。
ただし、機械学習での最急降下法も確率的勾配降下法もこれとほぼ発想は同じなので、この例題を最急降下法で解ければ機械学習の確率的勾配降下法もほぼマスターできるはずです。
ラグランジュ未定乗数法
余談ですが、この例題も理論的にきれいに解くことができます(もちろん平方完成でも解けます)。制約条件のないラグランジュ未定乗数法と捉えられます。
ラグランジアンは、
$$L = x^2 -2x+4y^2$$
xとyで偏微分すると、
\begin{align}
\frac{\partial L}{\partial x} &= 2x-2 =0 \\
\frac{\partial L}{\partial y} &= 8y = 0
\end{align}
よって$x=1, y=0$となります。ラグランジュ未定乗数法結構なんでもいけるので自分は好きです。ここでも**(偏)微分=0を使っているのを再確認できます**ね。
機械学習の最急降下法と確率的勾配降下法
2変数関数の最急降下法とほぼ同じです。機械学習の場合はステップが目的関数について解かないでもいけます。
機械学習の最急降下法も確率的勾配降下法も、和の形の目的関数を最小化する問題を扱います。確率的勾配降下法そのものについてはもっと良い説明がいっぱいあるので軽くさらうだけにします。
$$Q(w) = \sum_{i=1}^n Q_i(w) $$
これをループごとにバカまじめに
$$w := w-\eta\sum_{i=1}^n \nabla Q_i(w) $$
Σの中を全部計算するのを最急降下法(バッチ学習)、英語ではtotal gradient descentといいます。
対して、Qiをループごとにシャッフルして(ここがポイント)、シャッフルしたQiに対して
$$w := w-\eta \nabla Q_i(w) $$
とアップデートしながら反復するのを確率的勾配降下法、英語ではstochastic gradient descentといいます。どちらの降下法についても、ηを学習率といい、収束の有無や発散を決める最重要パラメーターです。
シャッフルすることが確率的で、シャッフルによって局所解にハマりにくくなるのが売り(らしい)。
確率的勾配降下法が局所解に陥らないことを保証するものではない
さて、確率的勾配降下法のWikipediaにこのようなことが書いてあります。
確率的勾配降下法の収束性は凸最適化と確率近似の理論を使い解析されている。目的関数が凸関数もしくは疑似凸関数であり、学習率が適切な速度で減衰し、さらに、比較的緩い制約条件を付ければ、確率的勾配降下法はほとんど確実に最小解に収束する。目的関数が凸関数でない場合でも、ほとんど確実に局所解に収束する
なぜこの点が気になったのかというと、ネットで探していると、大域的な最適解に収束する条件をすっ飛ばして「最急降下法は局所解に陥るが、確率的勾配降下法なら陥らない(極端な意訳)」というのを見て、自分は「???」となったからです。確かにこのWikipediaの表記もよく知らないで見ると、自分のように曲解するリスクはあるかもしれません。
実際前述の4次関数
$$y=x^4-4x^3-36x^2 \tag{1}$$
に対して、学習率を0.0001として、最急降下法と確率的勾配降下法のどちらで計算しても、初期値のxをプラスにするとx=6の大域的な最適解に収束しました。しかし、初期値のxをマイナスにしてしまうとx=-3の局所解に収束してしまいました(学習率の設定によっても変わるかもしれません)。なぜこれが確率的勾配降下法で計算できるかというと、確率的勾配降下法では、
$$Q(w) = \sum_{i=1}^n Q_i(w) $$
のように和の形で表される目的関数の最小化を行いますが、この4次関数は多項式なので、
\begin{align}
Q_1(w)&=w^4, Q_2(w)=-4w^3, Q_3(w)=-36w^2 \\
Q(w) &= Q_1(w) + Q_2(w) + Q_3(w)
\end{align}
とおいてしまえば、ループのたびに関数をシャッフルして確率的勾配降下法と同等のアプローチが使えたからです。局所解に収束した理由は単純で、(1)の4次関数が凸関数でないからです。関数fが凸関数であるとは、任意の$a,b$、$0\leq\lambda\leq1$を満たす任意の実数$\lambda$に対して以下の不等式を満たすものです。
$$\lambda f(a) +(1-\lambda)f(b)\geq f(\lambda a+(1-\lambda)b)$$
より直感的に捉えるなら、グラフ上の2点を通る直線を引いて、グラフがその直線の常に下にあるなら凸関数ということです。
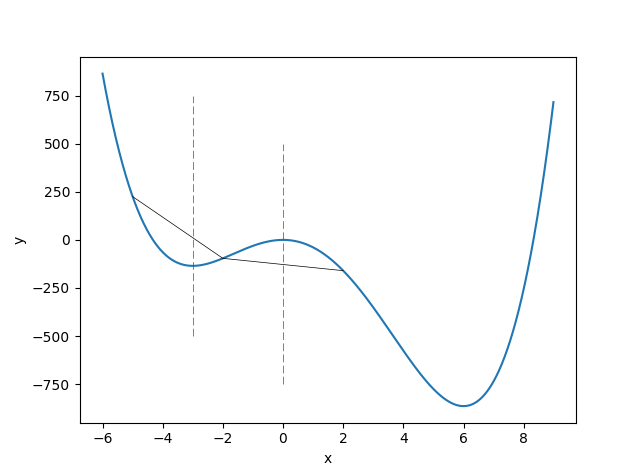
x=-5→x=-2で引いた直線に対してグラフは常に下にありますが、x=-2→x=2ではグラフは直線の上にあります。x全体で見ればこの4次関数は凸関数ではありません。
つまり、極小値を探していけば結果的に大域的な最小値が見つかるというのは、目的関数が凸関数であるからというのが大前提にあるためで、勾配降下法が確率的かそうでないかというのが決定づけているのではありません。
確率的勾配降下法が最小解に収束する条件というのを探していましたが、原著の論文を当たらないとよくわかりませんでした(課金がいる)。AT&T研究所が出している論文は無料で読むことができ、最急降下法の局所解についてWikipediaより丁寧な説明がありました。
L´eon Bottou, "Stochastic Gradient Learning in Neural Networks" p.4より
The total gradient (3) converges to a local minimum of the cost function. The algorithm then cannot escape this local minimum, which is sometimes a poor solution of the problem.
In practical situations, the gradient algorithm may get stuck in an area where the cost is extremely ill conditionned, like a deep ravine of the cost function. This situation actually is a local minimum in a subspace defined by the largest eigenvalues of the Hessian matrix of the cost.
The stochastic gradient algorithm (4) usually is able to escape from such bothersome situations, thanks to its random behavior (Bourrely, 1989).
ここでいうThe total gradientとはバッチ学習での最急降下法です。『最急降下法では、局所解から逃げることはできないが、確率的勾配降下法(stochastic gradient)は乱数の挙動のおかげで局所解から脱出することができる』と書かれています。確かに、「確率的勾配降下法が局所解に陥らないことを断言はできないが、それでも脱出できる可能性はある」ぐらいの言い回しなら納得できます。
確率的勾配降下法のメリットとは?~最小二乗法で考える~
では確率的勾配降下法の具体的なメリットは何でしょうか?例えば収束の際の精度がよくなるとか、最急降下法では越えられなかった局所解を乗り越えて別の最適解にたどり着くとか、収束までのループが少なくなるとかそういう具体的な指標が欲しいのです。
ここでは単回帰分析の最小二乗法の例に取ります。最小二乗法についてはなんとなく理解している人が多そうなので説明は省略します。
参考:最小二乗法
回帰分析の最小二乗法
単回帰分析では、
$$ \hat{y_i} = \alpha x_i + \beta + \epsilon\qquad \epsilon\sim N(0,\sigma)$$
とyをxで推定。ここでεは正規分布に従う誤差項です(ただのノイズなので気にしなくて良い)。ここで目的関数は、訓練データの実測値$y_i$と推定値$\hat{y_i}$の差の2乗和ですから、
$$ Q = \sum_{i=1}^n (y_i-\alpha x_i-\beta)^2 $$
を最小化するαとβを選びます。これを展開すると次のようになります。
$$ Q = \sum_{i=1}^n (x_i^2\alpha^2 + \beta^2+2x_i\alpha\beta-2x_i y_i\alpha -2y_i\beta+y_i^2) $$
ぱっと見怖い式が出てきましたが恐れることはありません。$\sum x_i$や$\sum y_i$は全てデータから計算できるので、ただの数値です。そう考えるとこれはαとβの2次関数です。Σの中身はただの数値なのでこう置き換えましょう。
\begin{align}
\sum x_i&=s_x, \sum y_i=s_y \\
\sum x_i y_i &= s_{xy} \\
\sum x_i^2 &= s_{xx}, \sum y_i^2 = s_{yy}
\end{align}
すると
$$ Q = s_{xx}\alpha^2+n\beta^2+2s_x\alpha\beta-2s_{xy}\alpha-2s_y\beta+s_{yy}$$
αとβで偏微分し、
\begin{align}
\frac{\partial Q}{\partial\alpha} &= 2s_{xx}\alpha+2s_x\beta-2s_{xy} \\
\frac{\partial Q}{\partial\beta} &= 2n\beta+2s_x\alpha-2s_y
\end{align}
勾配ベクトルを行列表記すると、
\frac{\nabla Q}{2} = \begin{pmatrix} s_{xx} & s_x \\ s_x & n \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix} - \begin{pmatrix} s_{xy} \\s_y \end{pmatrix}
となります。これは先程のラグランジュ未定乗数法を使えば理論的に求まります(Qをαとβで偏微分して=0の連立方程式を解く)。暇な方は解いてみてください。
最小二乗法は凸関数
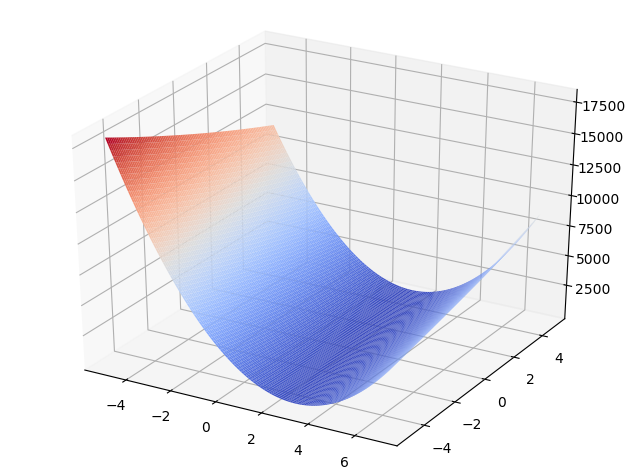
α=2、β=1(つまりy=2x+1)、ノイズは標準正規分布N~(0,1)に従う乱数としたときに、データ数10の場合の目的関数の3次元グラフを書くと次のようになります。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
np.random.seed(114514)
# y = 2x + 1 + e, e~N(0,1)とする
# α=2, β=1を推定する(実際はこのα、βは未知の値)
x = np.arange(10)
y = 2*x + 1 + np.random.standard_normal(10)
s_x = np.sum(x)
s_y = np.sum(y)
s_xy = np.sum(x*y)
s_xx = np.sum(x**2)
s_yy = np.sum(y**2)
def ols(a, b):
global x
global s_x, s_y, s_xx, s_xy, s_yy
return s_xx*a**2 + len(x)*b**2 + 2*s_x*a*b - 2*s_xy*a - 2*s_y*b + s_yy
alpha = np.arange(-5,7,0.1)
beta = np.arange(-5,5,0.1)
A, B = np.meshgrid(alpha, beta)
L = ols(A, B)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(A, B, L, rstride=1, cstride=1, cmap=cm.coolwarm)
plt.show()
グラフの断面が2次関数であることに注目してください。やっていることは最初に出した2次関数の最小値を求めることの延長線上で、2変数に拡張しただけです。
グラフを見た感じ凸関数っぽいですよね。数値解法に行く前に最小二乗法の目的関数Qが凸関数であることを示しておきましょう。非常に美しい証明で、解いていて「おっ!?」となったのでぜひ味わってください。
関数Qが凸関数であるとは、ヘッセ行列$\nabla^2 Q$が半正定値であることと同値です。ヘッセ行列とは勾配ベクトルをもう一度偏微分したものです(なので∇の次数が2になっています)。
この関数Qのヘッセ行列は、
\nabla^2Q=\begin{pmatrix}\frac{\partial^2 Q}{\partial\alpha^2} & \frac{\partial^2 Q}{\partial\alpha\partial\beta} \\ \frac{\partial^2 Q}{\partial\beta\partial\alpha} & \frac{\partial^2 Q}{\partial\beta^2}\end{pmatrix}=2\begin{pmatrix}s_{xx} & s_x \\ s_x & n\end{pmatrix}
ある行列が半正定値行列であることを示すには、以下のリンクで記されている4つの性質のうち1つを満たせばよいです。
ここでは2次形式が負ではないことを示します。2次形式を使って書くと、
\begin{align}
& 2\begin{pmatrix}\alpha & \beta\end{pmatrix}\begin{pmatrix}s_{xx} & s_x \\ s_x & n\end{pmatrix}\begin{pmatrix}\alpha \\ \beta\end{pmatrix} \\
&= 2\begin{pmatrix}s_{xx}\alpha+s_x\beta & s_x\alpha+n\beta \end{pmatrix} \begin{pmatrix}\alpha \\ \beta\end{pmatrix} \\
&= 2(s_{xx}\alpha^2 +2s_x\alpha\beta +n\beta^2)
\end{align}
ここで$\sum_{i=1}^{n} x_i=s_x, \sum_{i=1}^{n} x_i^2=s_{xx}$とおいたことを思い出します。
\begin{align}
&= 2(\alpha^2\sum_{i=1}^nx_i^2+2\alpha\beta\sum_{i=1}^nx_i+n\beta^2) \\
&= 2\sum_{i=1}^n(\alpha^2x_i^2+2\alpha\beta x_i+\beta^2) \\
&= 2\sum_{i=1}^n(\alpha x_i+\beta)^2 \geq 0
\end{align}
したがって、最小二乗法の目的関数Qのヘッセ行列は半正定値、つまりQは凸関数となります。つまり、最小二乗法の局所解は大域的最適解としてよいことがわかります。
続いて、数値的に最急降下法、確率的勾配降下法を使っても解いて、結果を比較してみましょう。
最急降下法(TGD)の実装
def tgd(w0):
global x, y
global s_x, s_y, s_xx, s_xy, s_yy
# η=0.01とする
eta = 0.01
# 極小値を求める関数は Q(x,z) = s_xxα^2 + nβ^2 + 2s_xαβ - 2s_xyα - 2s_yβ + s_yy
# δQ/δα = 2s_xxα + 2s_xβ - 2s_xy
# δQ/δβ = 2nβ + 2s_xα - 2s_y
i = 1
w_before = w0
while True:
# 勾配ベクトル
grad = np.dot(np.array([[2*s_xx, 2*s_x], [2*s_x, 2*len(x)]]), w_before) - np.array([2*s_xy, 2*s_y])
#print(grad)
# 最急降下法でxを更新
w_after = w_before - eta / i * grad
# 収束したら(w_t+1 - w_t が十分小さくなったら)終了
if (np.abs(w_before - w_after) < 1e-5).all():
#print("反復終了")
return w_before, i
# 反復継続する場合
#print(i, "回目 w = ", w_before, "->", w_after)
i += 1
w_before = w_after
初期のηはサンプルにあわせて調整してください(収束速度が変わります)。和の部分は行列内積で計算しているので結構速いです。収束判定は「α,βの変化量がともに一定値(1e-5)未満になったら」で判定しています。この閾値を小さくすると精度は良くなりますが、収束に時間がかかります。
確率的勾配降下法(SGD)の実装
def sgd(w0):
global x, y
# η=0.01とする
eta = 0.01
# 極小値を求める関数は Q(x,z) = s_xxα^2 + nβ^2 + 2s_xαβ - 2s_xyα - 2s_yβ + s_yy
# δQ/δα = 2s_xxα + 2s_xβ - 2s_xy
# δQ/δβ = 2nβ + 2s_xα - 2s_y
i = 1
w_before = w0
indexes = np.arange(len(x))
np.random.seed(114514)
while True:
# インデックスをシャッフルする
np.random.shuffle(indexes)
w_tmp = w_before
for j in indexes:
# 勾配ベクトル
grad = np.dot(np.array([[2*x[j]**2, 2*x[j]], [2*x[j], 2]]), w_tmp) - np.array([2*x[j]*y[j], 2*y[j]])
#print(grad)
# 最急降下法でxを更新
w_after = w_tmp - eta / i * grad
w_tmp = w_after
# 収束したら(w_t+1 - w_t が十分小さくなったら)終了
if (np.abs(w_before - w_after) < 1e-5).all():
#print("反復終了")
return w_before, i
# 反復継続する場合
#print(i, "回目 w = ", w_before, "->", w_after)
i += 1
w_before = w_after
基本的にはTGDと変わりませんがシャッフルしているのがポイント。シャッフル以下のループ部分をforで書いているのでTGDより遅いです。ここを最適化するか、scikit-learnの組み込みのSGDを使ってください(あくまで理解用なので)。
TGDvsSGDの比較
解(α=2、β=1)の近傍で初期値を変化させてTGDとSGDの結果を比較します。$-1\leq\alpha_0\leq5, -2\leq\beta_0\leq4$でそれぞれ1刻みで動かしています。結果のシリアライズ用にMessagePackを使っています。
import umsgpack
result = {}
for m in range(2):
method = {}
method["param"] = []
method["ans"] = []
method["length"] = []
method["iter"] = []
for a0 in np.arange(-1,6):
for b0 in np.arange(-2,5):
print(a0, b0)
if(m == 0): itemv, itemi = tgd([a0, b0])
else: itemv, itemi = sgd([a0,b0])
method["param"].append((int(a0), int(b0) ))
method["ans"].append([float(itemv[0]), float(itemv[1])])
method["length"].append(float(ols(*itemv) ))
method["iter"].append(int(itemi))
if(m == 0): result["tgd"] = method
else: result["sgd"] = method
with open("regression.msg", "wb") as fp:
fp.write(umsgpack.packb(result))
比較するのは次の3点です。学習率や収束判定はTGD、SGDともに共通です。
- 推定値:真の値α=2,β=1に近いほどよい
- 距離:推定値を目的関数に代入したときの値。誤差の大きさを示す。
- 繰り返し回数:収束までに要した反復回数。少ないほどよい
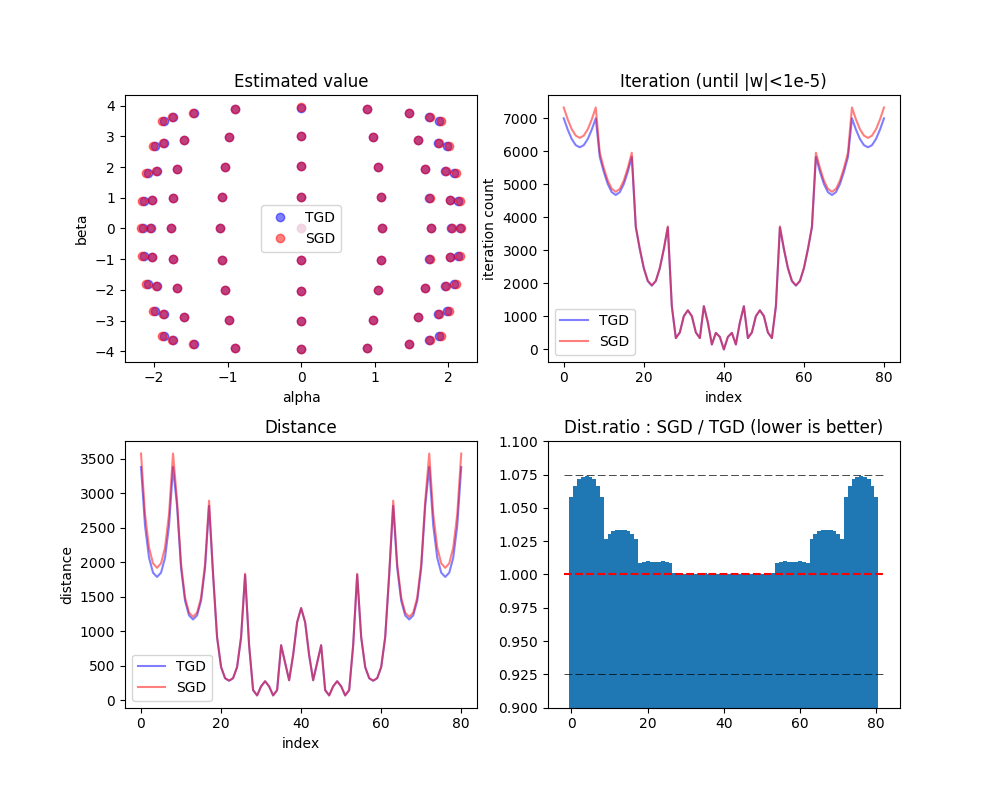
結果
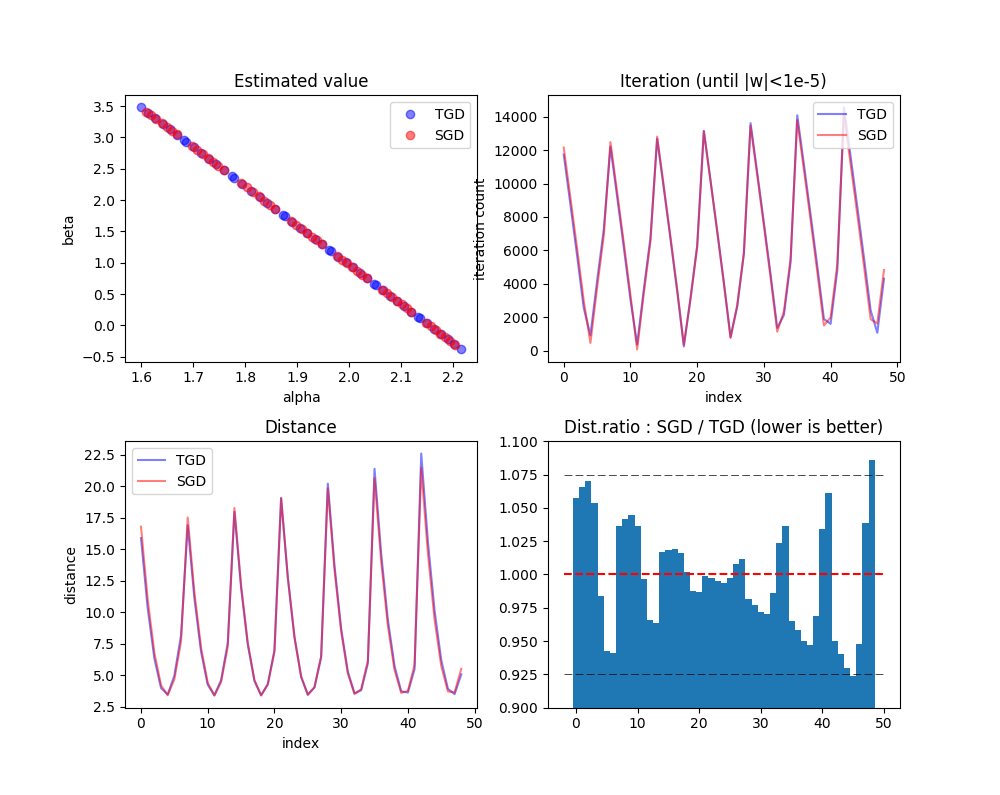
左上から、推定値をα(横軸)、β(縦軸)でプロットしたものです。真の値(α=2,β=1)が中心とはなりませんでしたが、SGDのほうがTGDよりも密になっている(点がぎゅっと集まっている)ので、SGDのほうがより精度が高いことがわかります。
右上は繰り返し回数を示します。見づらいかもしれませんが、SGD>TGDとなる点もTGD>SGDとなる点もある一方で、若干SGDのほうがトータルでは低いように見えます。サンプル単位で繰り返し回数をTGD,SGDで比較したところ、49サンプル中、繰り返し回数がTGDのほうがSGDより少なかったのが21サンプル、逆にSGDのほうがTGDより少なかったのが28サンプルとなりました。この例の場合は、1.3倍ほどSGDのほうが優勢となりました。
左下は同様に距離を示します。距離と繰り返し回数は全く同じで、距離が大きいところでは繰り返し回数も多かったです(なので収束判定において、目的地に近づいたことよりも、反復数が増えて学習率が減衰していったために1回のステップが限りなく小さくなったことのほうが支配的かもしれません)。49サンプル中、SGDのほうがTGDより距離が小さかったのは28サンプル、逆は21サンプルでした。また、距離の平均はTGD=8.471、SGD=8.421でSGDのほうが平均的に距離が小さくなりました。
右下は距離について、SGD÷TGDの比率を計算したものです。1より低ければその初期値に対する収束結果の距離についてSGDのほうが良い結果を出している、1より大きければTGDのほうが良い結果を出していると言えます。0.925、1、1.075に補助線を引いてみましたが、全般的に下に寄っていますよね。なのでここからも、この例の場合はSGDが優勢であったことが確認できます。
以下のコードで確認できます。
with open("regression.msg", "rb") as fp:
result = umsgpack.unpack(fp)
ans_tgd = np.array(result["tgd"]["ans"])
ans_sgd = np.array(result["sgd"]["ans"])
len_tgd = np.array(result["tgd"]["length"])
len_sgd = np.array(result["sgd"]["length"])
iter_tgd = np.array(result["tgd"]["iter"])
iter_sgd = np.array(result["sgd"]["iter"])
print(len_tgd)
print(len_sgd)
print(len_tgd - len_sgd > 0)
print(np.bincount((len_tgd - len_sgd) > 0))
print(np.bincount((iter_tgd - iter_sgd) > 0))
print(np.mean(len_tgd), np.mean(len_sgd))
全てにおいて確率的勾配降下法が有利?→そうとも限らない
なら全部の最適化で確率的勾配降下法のほうが最急降下法より有利かと言ったらそうでもありません。深くは触れませんが凸関数の制約を外して、
$$ \hat{y_i} = \alpha^2 x_i + \beta^2 + \epsilon$$
$$ Q = s_{xx}\alpha^4+n\beta^4+2s_x\alpha^2\beta^2-2s_{xy}\alpha^2-2s_y\beta^2+s_{yy}$$
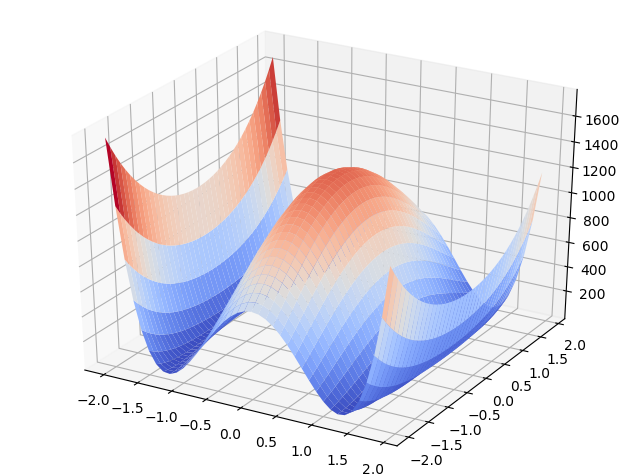
このように$\alpha^2, \beta^2$についての最小二乗法で解いてみると、TGDのほうが良い結果を出しました(単に収束まで至っていないのかもしれない)。この関数のグラフとサマリーだけ張っておきます。αもβも-4~4まで1刻みで動かしました。初期の学習率は0.00001としました(通常の最小二乗法と同じ初期値を使うと発散してしまいました)。
この場合は明らかに凸関数ではない(cf.最初の例の4次関数が凸関数ではない)ので、最小二乗法の最適化とはまた違うのかもしれません。確率的勾配降下法のほうが明らかに有利になる具体例というのがあれば興味がありますね(前節の最小二乗法の場合は1反復=全てのシャッフルされたサンプルを反映し終わったで見ているので、繰り返し回数が減らなければ計算量面でのメリットはありません)。
まとめ
冒頭の疑問は「確率的勾配降下法の具体的なメリットはなんだろう」でしたが、最小二乗法を通じて最急降下法(TGD)と確率的勾配降下法(SGD)の両方のアルゴリズムで比較を行うことで、SGDのほうが数値的に良い結果を出すことがあるというのが確認できました。全ての最適化において言えるまでは至っていませんが、具体的に良くなる例を確認できたことは有意義だったと思います。
そもそも数値計算自体、大域的な最適解(best)を出すものではなく、最適解に近いより良い局所解(more better)を出すものと考えれば、局所解自体が悪いわけではないのかと思います(局所解から出られなくなることや、局所解を最適解と誤検出することが問題)。凸関数?なにそれおいしいの?というレベルで複雑な1モデルで局所解が100や200ある場合は、その中から最良のものを選ぶのではなく、よりよいものを選ぶほうが現実的かと思います。あくまで人間的な手法なので。
理論的に数式変形をして解くのが神様の視点であるのに対して、コンピューターを使った数値計算が人間的な視点であると述べましたが、「神はサイコロを振らない(振らなくてもよい)のかもしれないが、人間はサイコロを振ったほうが有利になることがある」というのはなかなか面白い結論だと思います。
-
あまり縁がなさそうに思えるが、正規分布の元になっているガウス関数を足し算で組み合わせれば1変数関数でも大量に局所解のあるグラフを簡単に作り出すことができる。 ↩