ここでは、はじめてのパターン認識第7章について解説を行う。
- 7.1.1~7.1.3については線形分離可能なケースに限定した記述で、実際使う際はほぼ非線形で関係ないため割愛する
ニューラルネットワーク
ニューラルネットワークとは、端的に言えば人の脳仕組みを模した分類機である。
具体的に言えばたくさんの素子(脳におけるニューロン)を接続して階層上のネットワークを構築し、そこから出力を得るというアイデアだ。このネットワークはパーセプトロンと呼ばれている。
さて、実際にはデータを用いてパーセプトロンを学習させ、適切な分類が行えるようにしたい。では、学習させるということは具体的にどういうことになるのか。
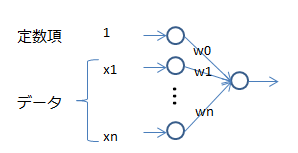
まず、パーセプトロンを構成する各ニューロンを、以下のようにモデル化する。
入力されるデータを$x=(x_0 = 1, x_1, ... x_n)$とし、それに対する重みを$w=(w_0,w_1,...w_n)$とする。そうすると最終的に得られる出力$y$は$x \times w$で表すことができる。$x$と$w$はベクトルなので、正確に表せば$y = w^Tx$となる。
誤差伝播法
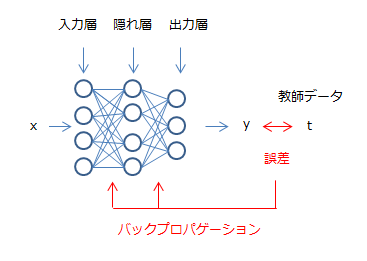
学習を行わせるというのは、与えられた学習データに合わせて重みである$w$の値を調整するということになる。この操作(学習データに合わせた重みの調整)が誤差伝播法(バックプロパゲーション)と呼ばれる手法である。
以下が、誤差伝播法のイメージ図である。実際のデータ$t$とニューラルネットワークから出力された$y$との差分が誤差であり、この誤差を各層をつなぐ重みに反映させている。
これを数式でモデル化すると以下のようになる。まず、使用する変数を定義しておく。
- 入力層$x$:$x_i(i=1...4)$で、これに定数項である1を加え$x=(1, x_1, ... x_4)$とする。
- 入力層->隠れ層への重み$w_{j}$:隠れ層のノード$V_j$から見ると自分への入力は$w_j^Tx$になる。
- 隠れ層$V$:$V_j (j=1...4)$
- 隠れ層->出力層への重み$w_{k}$:出力層のノード$y_k$から見ると自分への入力は$w_k^TV$になる。なお、計算時には$x$同様$V$にも定数項を加え、$V=(1, V_1, ... V_4)$として計算する(一つ上の層への入力を計算する際は定数項を加える)。
- 出力層$y$:$y_k (k=1..3)$
上記のとおり隠れ層$V_j$への入力(以下、$h_j$とする)は$h_j = w_j^Tx$となるが、ここで一つ技が入る。
実は、この状態だとどれだけ層を重ねても本質的には$y=ax+b$のような非常に単純な線形モデルと変わらない(変数と定数項に対し重みをかけて計算しているだけなので)。つまり、直線で分類できるような問題にしか対応できないことになる。
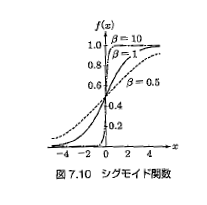
そこで、入力される値を非線形の関数$g$でラップすることにする。ここでよく使用されるのが、下記式で表されるシグモイド関数と呼ばれるものだ。
$$
g(u) = \frac{1}{1 + exp(- \beta u)}
$$
シグモイド関数は0~1の間で値を取る関数で、$\beta$の値が小さいほど中心の傾きが緩やかになり、線形的な動作になる(図7.10参照)。こいつで入力を包み込む、つまり$g(h_j)$が実際の入力となる。
出力層への入力は隠れ層同様$h_k=w_k^TV$となり、最後の出力層からの出力である$y$はこれを$g$でラップした$g(h_k)$となる。
これは、$V=g(h_j)$、$h_j=w_j^Tx$を代入して展開すると、$y=g(w_k^Tg(w_j^Tx))$となる。
ここまでが、$x$から$y$を導くための処理である。ここからは、$y$と$t$の間の誤差を計算し、それを各$w$に反映させる誤差伝播に入る($y$を計算していく処理をフォワードプロパゲーション、誤差を伝播していく処理をバックプロパゲーションという風に呼ぶ)。
まず、全体の誤差は以下のようにあらわせる(学習データがN個ある場合は各データについてこれを計算し、合算する)。
$$
E(w) = \frac{1}{2} \sum_{k=1}^K(t_k - y_k)^2
$$
これは単純に最終層からの出力である$y$と実際のデータである$t$との間の差である(マイナスの差異もあるため、二乗している)。
この誤差を最小化するには、当初言っていた通り各層の重み$w$を調整する必要がある。そのためには$w$を動かしたらどれぐらい影響があるのかを知る必要がある。具体的に言えば、各層の各ノードは最終的な誤差にどれくらい影響を与えるのか・・・ということだ。
これは誤差を重みで微分することで得られる(ざっくり言えば、重みによる微分は単位当たりの重みが誤差に与える影響を計算していると言える)。
実際計算すると・・・
出力層(第3層)
$$
\delta^{(3)} = (t - y)
$$
隠れ層->出力層(第2層)
$$
\delta^{(2)} = \frac{\partial E(w)}{\partial w_{k}} = \frac{\partial E(w)}{\partial y}\frac{\partial y}{\partial w_{k}} = (t - y) \times g'(h_k) V = \delta^{(3)} g'(h_k) V
$$
入力層->隠れ層(第1層)
$$
\delta^{(1)} = \frac{\partial E(w)}{\partial w_{j}} = \frac{\partial E(w)}{\partial V_j}\frac{\partial V_j}{\partial w_{j}} = \frac{\partial E(w)}{\partial y}\frac{\partial y}{\partial V_{j}} \frac{\partial V_j}{\partial w_{j}} = (t-y) \times w_k g'(h_k) \times g'(h_j) x = \delta^{(3)} w_k g'(h_j) x
$$
入力層->隠れ層では、第3層の誤差が隠れ層->出力層の間の重み$w_k$を通して$\delta^{(3)} w_k$として伝わっていることが確認できる。
これが誤差伝播法と呼ばれるゆえんである。
そして、誤差伝播法には以下のような特性がある。
- 局所最適解を多数持ち、どこの局所最適解に行くかは初期値に依存する。そのため、初期値に乱数を使用したりする
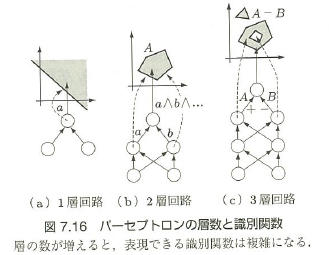
- 層が多いほど複雑な形状の分類を表現できるようになる。具体的には、一層の場合は線形(直線境界)、二層の場合は直線境界を組み合わせた凸領域、三層の場合はさらにその中に穴が開いたような形状を表現できる。しかし、層を増やすほど多数の局所最適解を持つようになり、探索が難しくなる(図7.16参照)
- 隠れ素子が多いと過学習が発生するため、どれくらいの数が適切なのかは精度を見ながら調整する必要がある。なお、過学習を防ぐために通常は正規化項の導入を行う。正規化項は$\lambda \sum_l^L w^{lT}w^{l}$、つまり係数の二乗に固定値$\lambda$をかけたものが利用される(ただし定数項への係数は除く)
上記の例では誤差の表現としてもっとも単純な二乗誤差を利用したが、他の式が使われることもある。
例えば最終的に出力する$y$を確率だとすると、その誤差は以下のようにあらわせる。
$$
E(w) = -tlog(y) - (1-t)log(1-y)
$$
学習データ$t$は0か1なので(発生したかしないか)、$t$が1のときは前の項、$t$が0の時は後ろの項しか残らない。
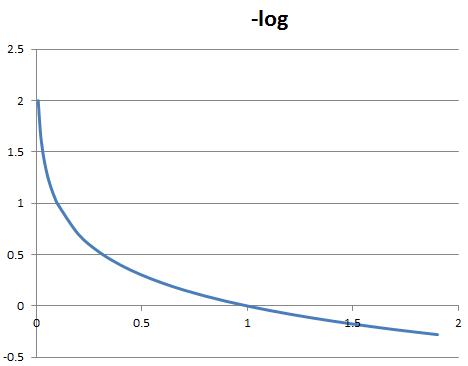
具体的に$-log(y)$と$-log(1-y)$が何を行っているかだが、これは対数関数の形状を見てみるとわかりやすい。
$t=1$とすると残るのは$-log(y)$となるが、この時$y$の値が小さくなるほど$-log(y)$の値は大きくなる。つまり実際は$t=1$、つまり発生しているにもかかわらず予測である$y$の値が0に近い、つまり起こりそうにないと予測している場合ペナルティが高くなる。これは$t=0$の場合の$-log(1-y)$にも言えることで、上記の関数$-tlog(y) - (1-t)log(1-y)$は要するに実態とかけ離れた予測をしている場合大きな値、つまり誤差が大きくなるような関数となっている。
まとめ
ニューラルネットワークを利用する場合には、以下点を考慮する必要がある。
- 誤差(目的関数)$E(w)$をどのように定義するか
- 非線形活性化関数に何を使うか(概ねシグモイド関数だが、バリエーション有)
- 層の数、隠れ層のノードの数を何個にするか。層を増やすほど複雑な形状を表現でき隠れ層を増やすほど精度は上がるが、その一方局所最適解が増える、過学習を起こすというデメリットも発生する。これはトレードオフであり、モデルの様子を見ながら調整する必要がある。