はじパタ全力解説: 第5章 k最近傍法(kNN法)

「はじめてのパターン認識」の第5章「k最近傍法(kNN法)」解説です。
最近傍法はAndrew Ng先生の機械学習入門コースになかった内容です。名前とイメージだけは知っていて詳しく調べたことがなかった最近傍法をようやく理解できました。
第4章に比べるとわかりやすく感じますが、私にとっては視覚的な内容をブログに書くのに時間がかかりました(最後はかなり省略していますが・・・)。第3章を理解している前提での内容でもあり、簡単なわけではありません。
はじめてのパターン認識 第5章 k最近傍法(k_nn法)が詳しく書いてくれていて非常に参考になりました。
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。

内容

5.1 最近傍法とボロノイ境界

最近傍法を概要レベルで理解すると図のようになります。

以下の式はk個のクラス、i番目クラスの学習データ数が$N(i)$個の場合です。最近傍法(Nearest Neighbor法)では、ユークリッド距離で計算します。学習データを鋳型(template)と呼びます(鋳型はクラス単位ではなく1件の観測データ単位です)。
※$d$は距離を示しています。

内容	式
K個のクラス	$\Omega=\{C_1, \cdots, C_k\}$
i番目のクラスの学習データ数	$N(i)$
i番目のクラスの学習データ数の集合	$S_i=\{x_1^{i}, \cdots, x_{N(i)}^{i}\}$
入力データ($x$)と学習データ($x_j^{(i)}$)の類似度 ユークリッド距離	$d(x,x_j^{(i)})=||x-x_j^{(i)}||$

以下が識別規則で$t$はリジェクトするためのしきい値です。$\min_{i,j} d(x,x_j^{(i)})$は、クラス$i$の中で一番近い観測データとの距離を示しています。

{  \begin{cases}
    \arg \min_i \{ \min_j d(x, x_j^{(i)})\} & \Leftarrow \min_{i,j} d(x,x_j^{(i)}) < t のとき \\
    リジェクト & \Leftarrow \min_{i,j} d(x,x_j^{(i)}) \ge t のとき \\
  \end{cases}
}

5.1.1 ボロノイ図

最近傍法のポイントは入力データに最も近い鋳型を見つけることです。鋳型ごとに自身の支配領域(その領域に観測データが入った場合に鋳型の属するクラスに識別)を持ち、その領域をボロノイ領域、その境界をボロノイ境界と呼びます。Wikipediaがわかりやすいです。
ボロノイ境界等を2次元、２つの鋳型で例示すると以下の図のようになります。

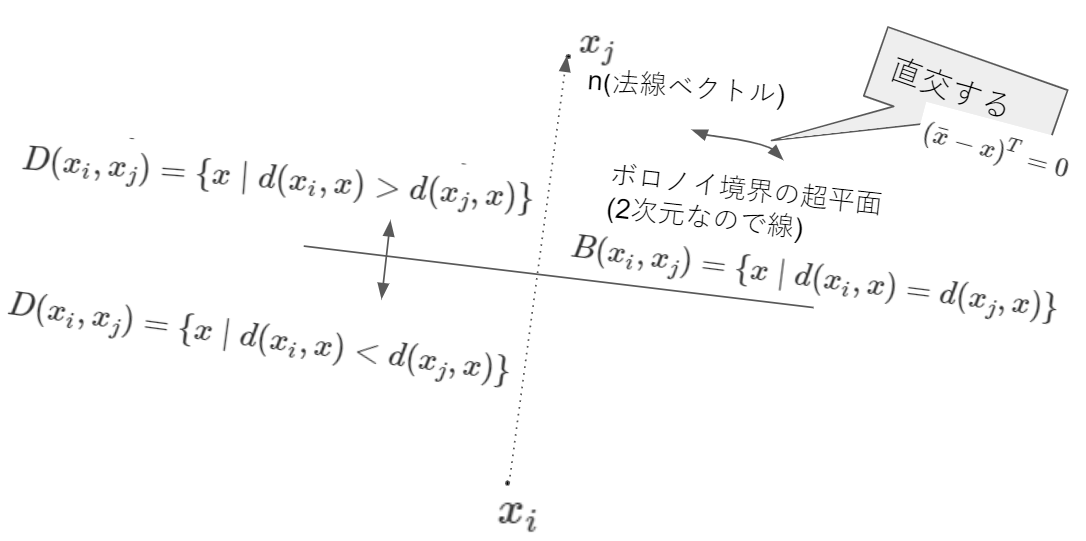
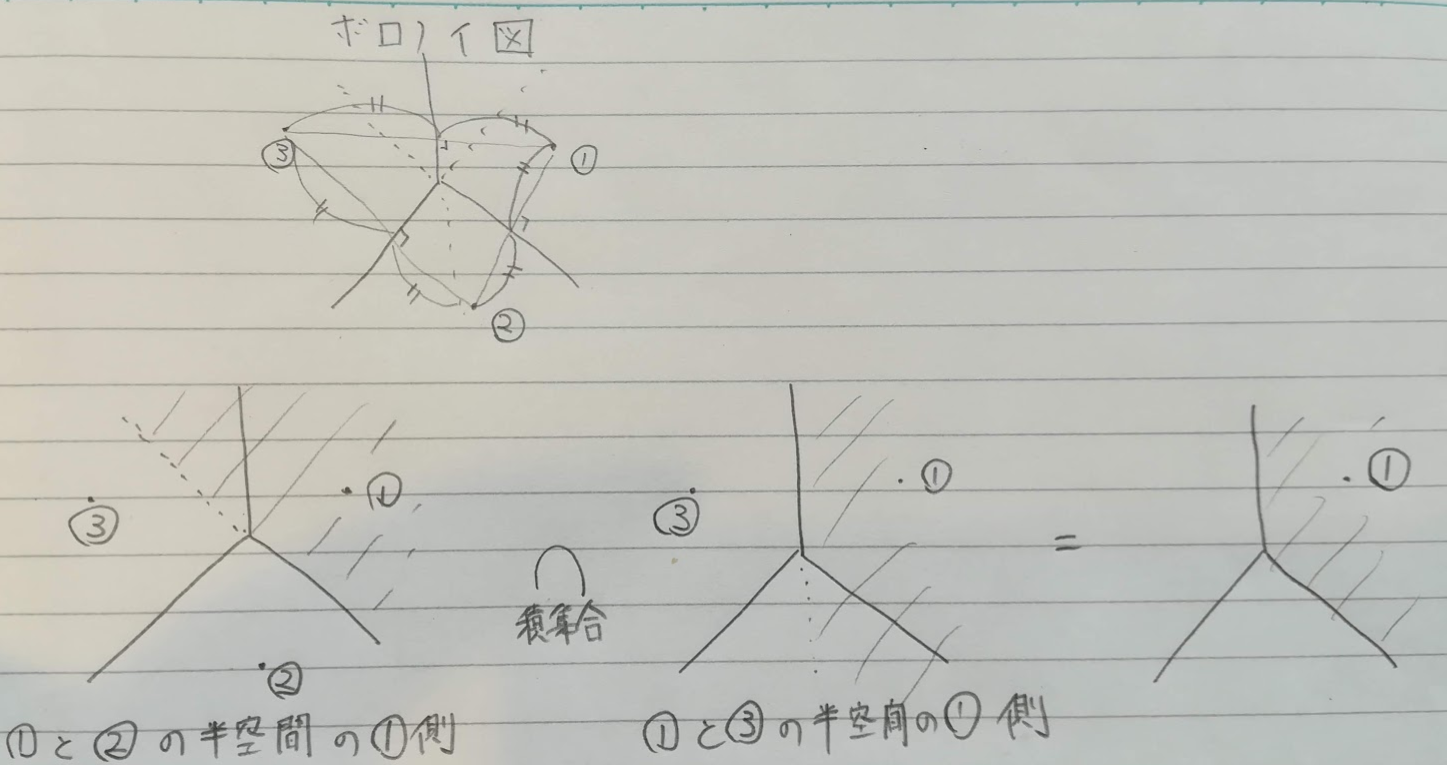
鋳型が3つ以上の場合の$x_i$のボロノイ領域は、各鋳型間の半空間の積集合は以下の式と図です(鋳型の集合を$S=\{x1, \cdots, x_N\}$とします)。

VR(x_i,S) = \displaystyle\bigcap_{x_j \in S, j \ne i}{D(x_i, x_j)}

(汚い図で恐縮ですが)3つの鋳型で例を書きました。

5.1.2 鋳型の数と識別性能

最近傍法は学習データ数が多いほど精度が向上します。

5.2 kNN法

最近傍の鋳型を近いものから$k$個とってきて、鋳型が最も多く所属するクラスに識別する方法をk最近傍法(kNN法)と呼びます。所属する鋳型数が同数の場合はリジェクトとする場合と、ランダムに決定する場合があります。
下図の例だと$k=3$としたら、クラス1よりクラス2に属する鋳型数が多いのでクラス2とし、$k=6$の場合は逆でクラス1に識別します。

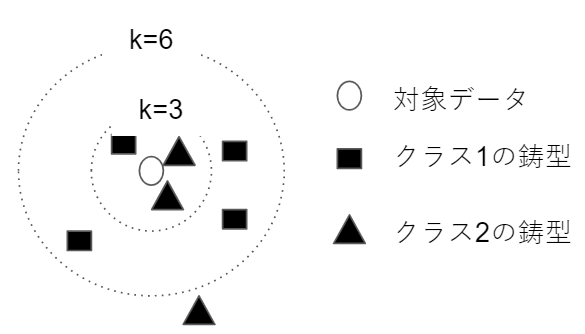
最近傍法の場合は、他クラスの鋳型に囲まれる孤立点ができます。kNN法にすると、多数決型なので一定程度の異常値を許容し孤立点が少なくなります。

5.3 kNN法とベイズ誤り率

kNN法とベイズ誤り率との関係です。
2値分類とした場合の仮想データで、ベイズ識別規則および1NN, 2NNの誤り率を出しました。

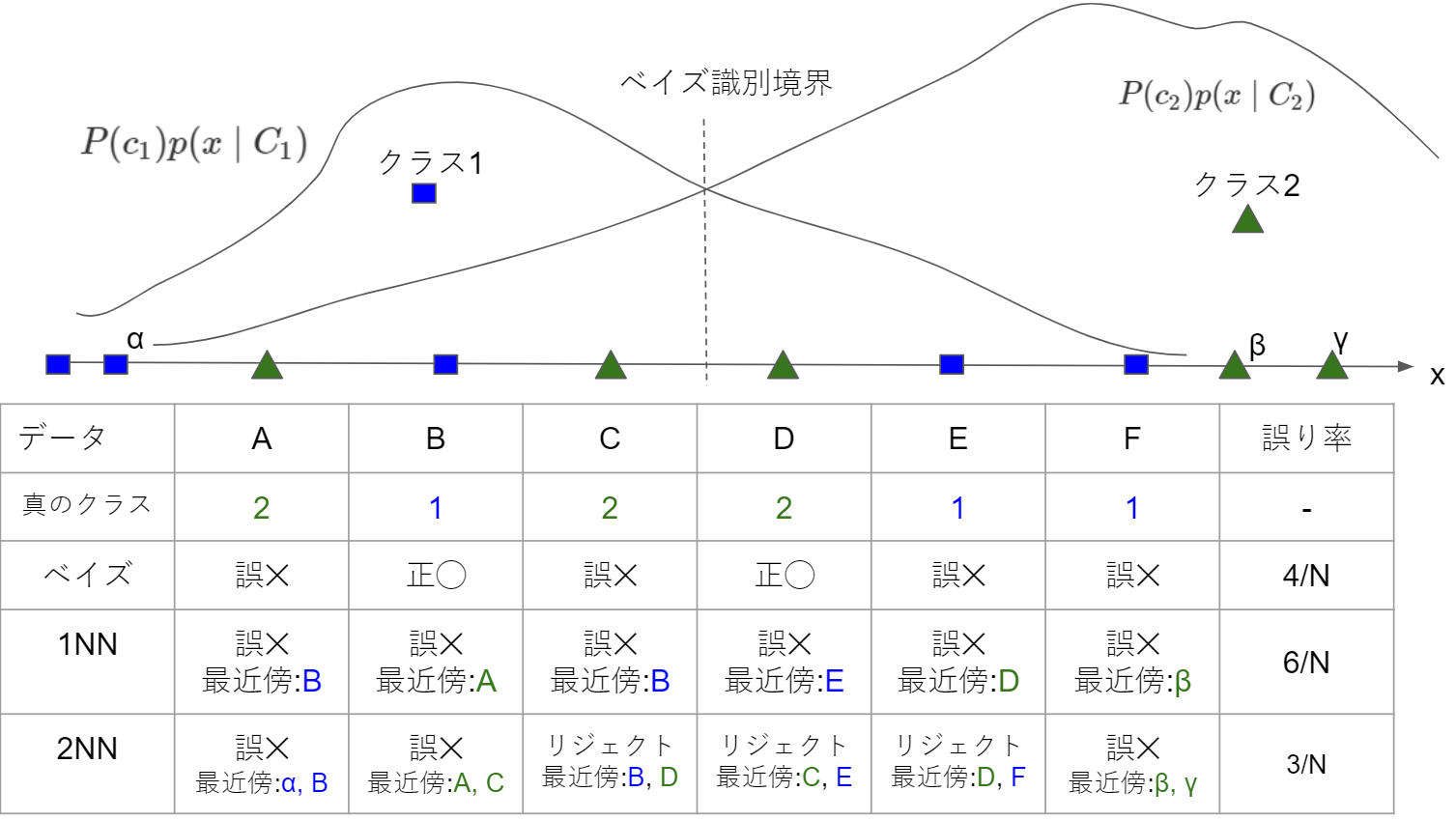
今回の場合は、誤り率について以下の大小関係となっています。これを一般化したときにどうなるかを見ていきます。

\hat{\epsilon}_{2NN} \leq \hat{\epsilon}^* \leq \hat{\epsilon}_{1NN}

5.3.1 漸近仮定とkNN誤り率の期待値

最近棒法の理想として鋳型の数が無限大にあるとするとします(この仮定を漸近仮定と呼ぶっぽい)。
入力$x$の最近傍鋳型を$x_{1NN}$とし、N個の鋳型の集合を$T_N$としたときに以下の式が成り立ちます。これは、「ユークリッド空間に無限に鋳型あれば、一番近い鋳型との距離は0」ってことです。

\lim_{N \to \infty} T_N \Rightarrow d(x, x_{1NN}) \rightarrow 0

その前提のもとに、kNN誤り率とベイズ誤り率との間に次の大小関係が成立します。

\frac{1}{2} \epsilon^* \le \epsilon_{2NN} \le \epsilon_{4NN} \le \cdots \le 
\epsilon^* \le  \cdots \le \epsilon_{3NN} \le \epsilon_{1NN} \le  2\epsilon^*

偶数NNが真ん中より左でNNの数が少ないほど誤り率が少ないです。
奇数NNは真ん中より右でNNの数が少ないほど誤り率が多いです。
私の理解では、二値分類で偶数NNの場合はリジェクトが起こる可能性があり、誤り率低下に寄与します。リジェクトはNNの数が少ないほど起きやすいので2NNが最も誤り率が少なくなりやすいです。逆に二値分類で奇数NNは、リジェクトが起きません。そのため、必ずベイズ誤り率よりも誤り率が高くなります。そして、鋳型が無限あると仮定するとNNの数が多い方が、誤りが起きにくいです。
証明部分の解説は省略します。

5.3.2 漸近仮定は成り立つか

次元数が多いと漸近仮定は成り立ちません。
第1章の「次元の呪いとサンプル間の距離」で書いたのですが、次元が多い場合にデータは近傍に集まらず遠い場所に集まってしまいます。そのため、$\lim_{N \to \infty} T_N \Rightarrow d(x, x_{1NN}) \rightarrow 0$とはなりません。

5.4 kNN法の計算量とその低減法

kNNは計算量が多く計算時に必要なメモリ容量も多いため、それらを低減する方法がいくつかあります。

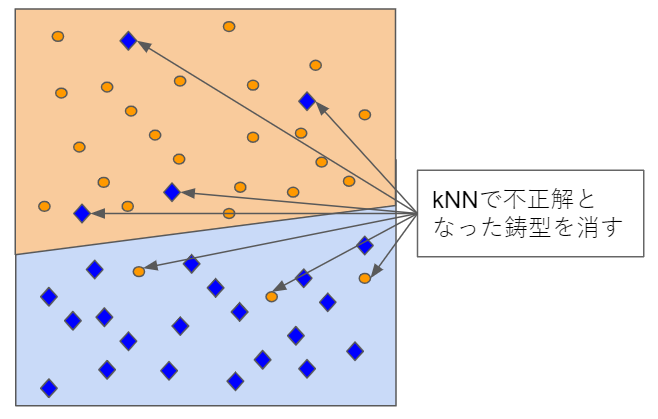
5.4.1 誤り削除型kNN

kNNで誤って識別されたデータを削除します。削除後に識別境界が変わるので再帰的に繰り返すことも可能です。

5.4.2 圧縮型kNN

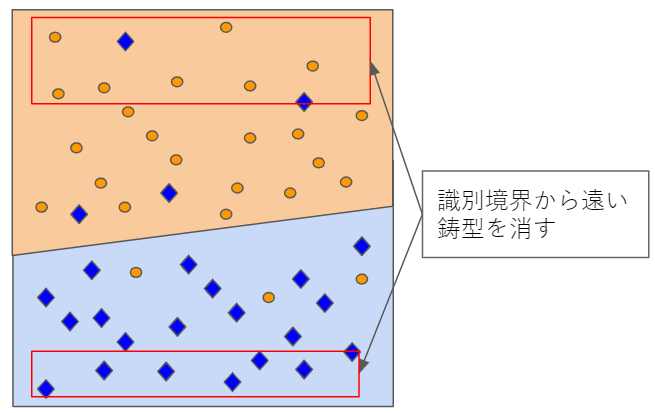
識別境界以外のデータはあまり重要ではないので消します。
消す際には、以下の条件付きベイズ誤り率が小さくなるようにします。

\epsilon(x) = min[P(C_1 \mid x), P(C_2 \mid x)]

5.4.3 分枝限定法

分枝限定法と呼ばれる探索方法があります(kNNに限らない手法のようです)。データを階層型クラスタリングで構造化します(「言語処理100本ノック-98本目」でやりました)。
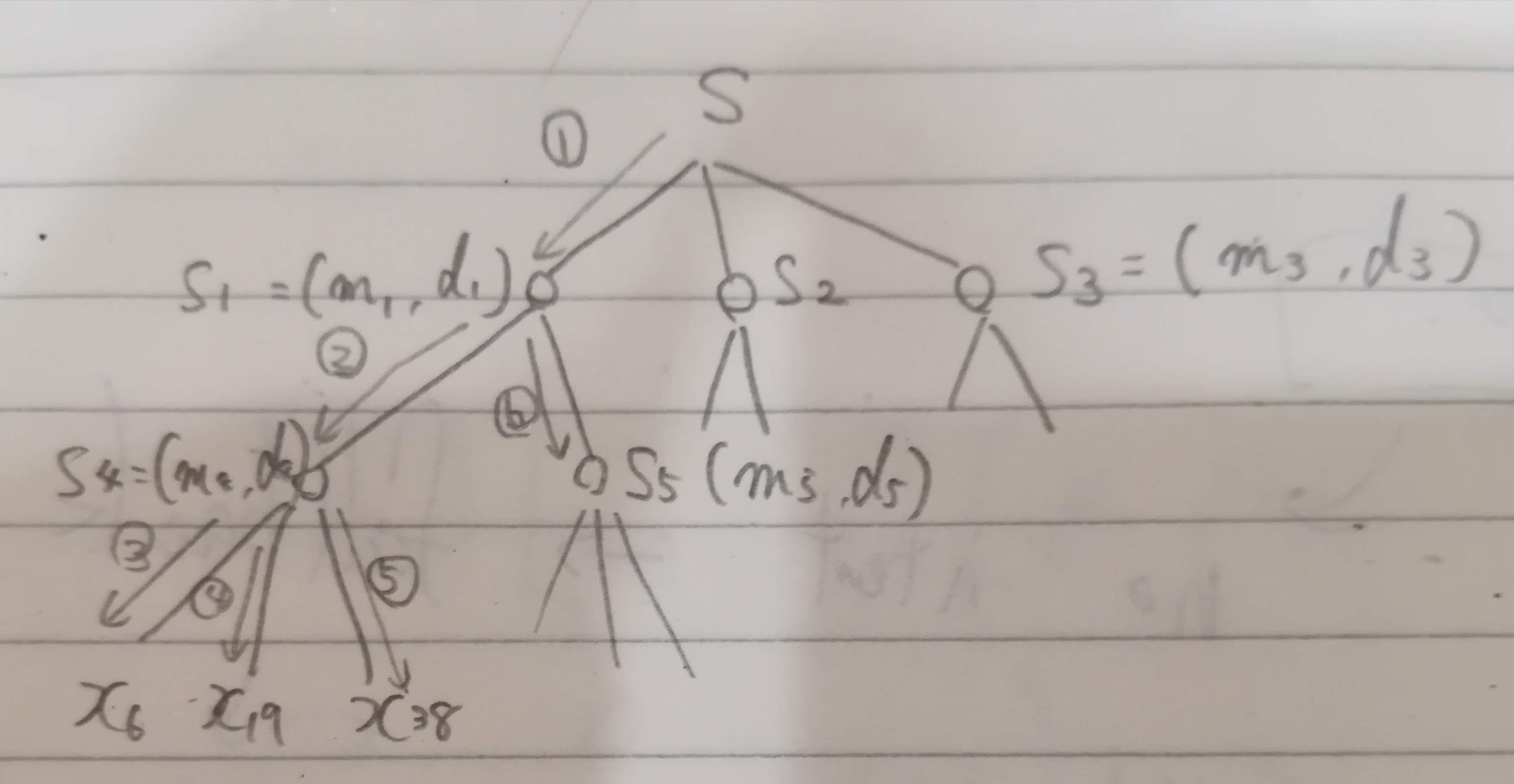
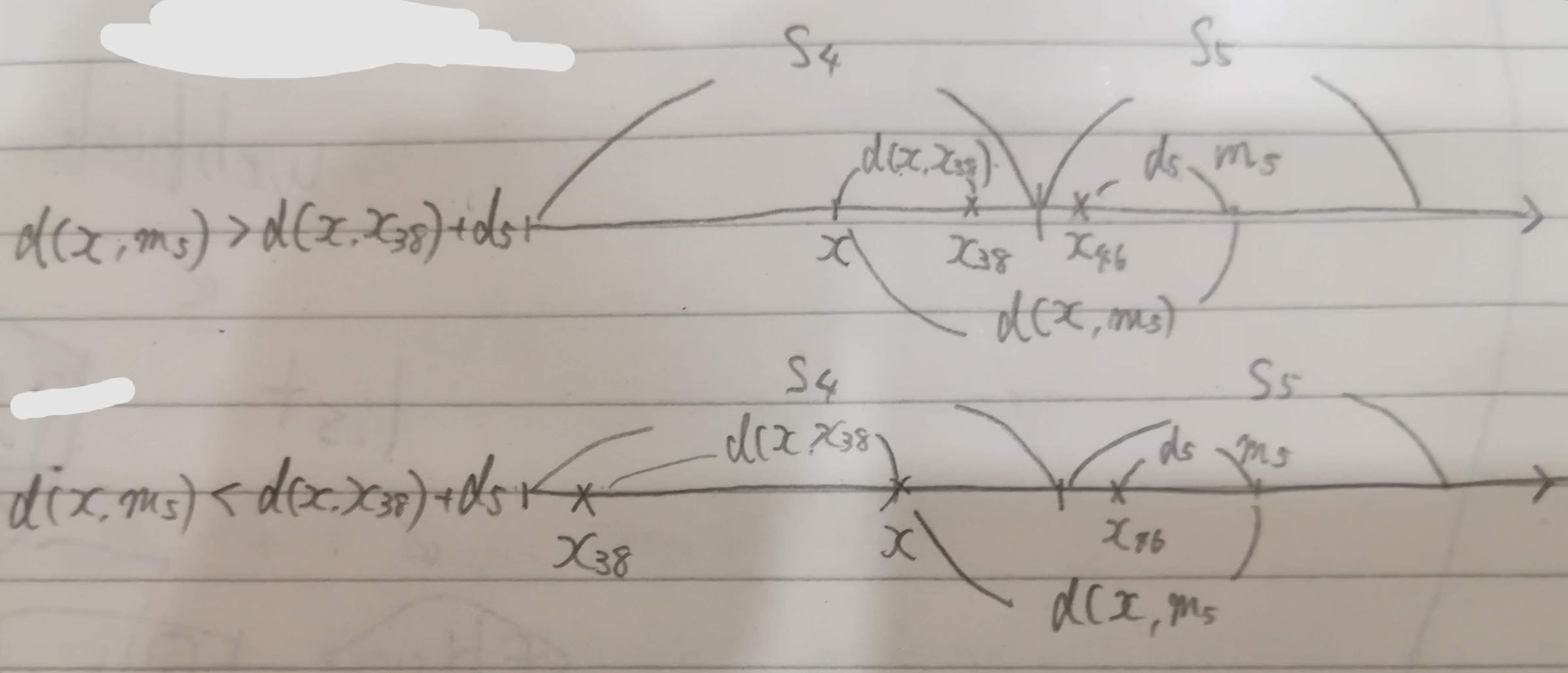
例えば、2次元のデータを階層型クラスタリングしたイメージ図です。最上位では$S_1, S_2, S_3$の3つに分け、$S_3をさらにS_4とS_5$に分けています。
ここでそれぞれのクラスタに平均ベクトル$m_i$(図の青の矢印)と平均ベクトルから最も遠いデータまでの距離$d_i$(図の緑の矢印)を計算しておきます。

そして、図のように探索をしていきます。

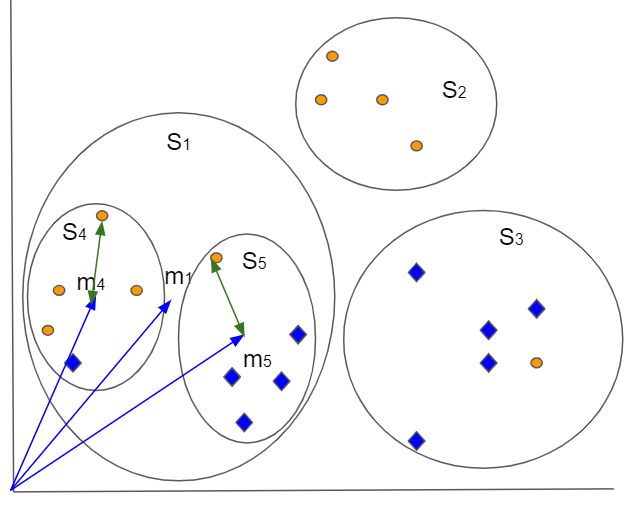
探索をしてクラスタ$S_4$に属する最も近い$x_{38}$を見つけた場合、クラスタ$S_5$に属するデータと比較する必要がないかを以下の計算式でチェックします。

d(x,m_5) > d(x, x_{38}) +d_5

すごい汚いですが、1次元で表すとこういうことです。

5.4.4 近似最近傍探索

自身のデータを$q$、各鋳型を近い順に$x_D, x_A, x_B, x_C, x_E$とします。$q$は$x_D$に所属。

1. 超空間を分割していく(分割した結果は二分木で表現できる)
2. 所属する超空間のデータとの距離を計算: $d(q, x_D)$を求める
3. 最も近い(データではなく)分割した超空間($A$)との距離($d(q, A)$)を計算
4. 現時点での最短なデータとの距離を$1+\epsilon$で割った値と超空間との距離を比較し、近似最近傍かを判断 あとは、判断結果によって3と4を繰り返します。

{  \begin{cases}
    x_Dが近似解 & \Leftarrow  \frac{d(1, x_D)}{1+\epsilon} \le d(q, A)\\
    次の超空間へ進む & \Leftarrow  \frac{d(1, x_D)}{1+\epsilon} > d(q, A) \\
  \end{cases}
}

(データではなく)領域までの大小関係が判断できれば、データに対する大小関係も成り立ちます。

d(q, x_D) < (1 + \epsilon) d(q, A) < (1 + \epsilon) d(q, x_A)

「はじパタ」勉強系記事リンク

章	項目	時間(h)	難易度	学んだこと
1	はじめに	8.9		特徴の型, 特徴空間, 次元の呪い
2	識別規則と学習法の概要	12		ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習
3	ベイズの識別規則	14.8		ベイズ識別規則, ROC曲線
4	確率モデルと識別関数	18		平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定
5	k最近傍法(kNN法)	8		最近傍法, ボロノイ境界, kNN
6	線形識別関数(前半)	30.4		正規方程式
6	線形識別関数(後半)	前半に時間は含む		フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰
7	パーセプトロン型学習規則	13.5		多層パーセプトロン, 誤差逆伝播法, シグモイド関数
8	サポートベクトルマシン	14.7		カーネルトリック, ν-SVM
9	部分空間法	15.4		主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法
10	クラスタリング	8.4		距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル
11	識別機の組み合わせによる性能強化	11.6		ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト