「はじめてのパターン認識」、通称「はじパタ」の第2章の解説です。
13ページ程度のくせに読み解くのに時間をかなりかけました・・・ 躓きポイントは2点あって、ブートストラップ法で書かれている計算式、最後のバイアス・分散分解です。マクローリン展開など文系人間にとっては難しい内容も含んでいて時間がかかります。
改めて機械学習のハードルの高さを感じますが、Coursera機械学習入門コースや数学勉強をしておいてよかったと改めて感じました!
※はじパタ勉強系は記事「文系社会人がはじパタで機械学習を数式含めて理解した奮闘記」にまとめました。
内容
2.1. 識別規則と学習法の分類
2.1.1. 識別規則の構成法
識別規則は、入力データ$x$からクラス$C_i \in \Omega = \{ C_1, \ldots, C_k \}$への写像である
さっそく理解し難い文が出てきました。入力データ$x$に識別関数を使うとクラスに分類される、という意味。
| 記号等 | 意味 | 例(じゃんけん) |
|---|---|---|
| $C_i$ | 1つのクラス(分類) | グーというクラス |
| $C_i\in \Omega$ | クラス$C_i$はクラス集合($\Omega$)を構成する元(要素) | じゃんけんというクラス集合の構成要素の1つにグーがある |
| ${C_1, \ldots, C_k}$ | 元(要素)は${C_1, \ldots, C_k}$ | グー・チョキ・パー |
| 写像(mapping) | 集合Aの各元(要素)がそれぞれ集合Bの元(要素)を唯一指定するような規則があるとき「AからBへの写像」と言う | 「5本の指の状態」からじゃんけん(グー・チョキ・パー)への写像 |
※$\Omega$ は大文字のオメガ
以下を参考にしました。
代表的な識別規則の構成法は以下の4つ(どうせ後で詳しく学習するので今はあまり調べない)。
| 識別規則構成法 | 内容 | 例 |
|---|---|---|
| 事後確率による方法 | パターン空間に確率分布を仮定し事後確率が最大のクラスに分類 | ベイズの最大事後確率法 |
| 距離による方法 | 入力ベクトル$x$と各クラスの代表ベクトルとの距離を計算し、一番近い代表ベクトルに分類 | 最近傍法 |
| 関数値による方法 | 関数$f(x)$の正負/最大値でクラスを決める | パーセプトロン型学習回路やSVM |
| 決定木による方法 | 識別規則の真偽に応じて次の識別規則を順次適用し、決定木の形でクラスを決める | - |
2.1.2. 教師付き学習
識別規則は入力データ(特徴ベクトル)からクラスへの写像を $y=f(x)$という関数を用いて表現する。識別規則の学習はこの$f()$を学習データを用いて決めることである。
線形識別関数
2クラス問題の線形識別関数は以下のように**線形関数(内積)**を用いて表現し、識別クラスは結果$y$の正負で決める。入力データが正しいクラスに対応するようにパラメータ$w$を調整。
y = f(x;w) = w_1 x_1 + \cdots + w_d x_d = w^T x
| 記号等 | 意味 |
|---|---|
| $w$ | $w$はweightの略で「重み」。パタメータとも呼ぶ。 |
| $f(x;w)$ | セミコロンの前($x$)は変数、後($w$)はパラメータ 特徴$x$を入力しパラメータ$w$を使った関数で出力 |
内積
「実数ベクトルの標準内積」とは以下のように定義されるようです。
※$\mathbb R^n$は実n次元数空間を意味する
x = \left[
\begin{array}{rrr}
x_1\\
x_2 \\
\vdots \\
x_d
\end{array}
\right],\,\,
w = \left[
\begin{array}{rrr}
w_1\\
w_2 \\
\vdots \\
w_d
\end{array}
\right]
\in \mathbb R^n
\\ (w, x) = w_1 x_1 + \cdots + w_d x_d
厳密な線形
$f(x) = b + wx$ は厳密な意味で線形ではない。
厳密に線形である場合は重ね合わせの原理 $f(ax)=af(x),,, f(x+y)=f(x)+f(y)$が成立する必要があるが定数項$b$があるので線形ではない。このような関数をアフィン関数と呼ぶ。
ただし、$b=w_0x_0(x_0 = 1)$と考えると線形関数になるので、$b$(定数項)があっても線形識別関数と呼ばれている。
教師データ
学習をするために入力データとそのクラスを指定したデータを対にした学習データが必要。クラスを指定したデータを教師データと呼びます。2クラスで正負とすると$t \in \{-1, +1\}$。クラス集合$t$の元(要素)は-1と+1という意味。
※$t$は教師データ(Teacher Data)の"t"っぽい。
クラス数が3つ以上ある場合はダミー変数表現を用いて、例えば4クラスの場合は$t=(0, 1, 0, 0)^T$のような教師データにする。このような教師データをK対1符号化(1-of-K coding)という。
学習に用いられるすべての入力と教師データの対の集合を教師データセットといい、$D_L$で表す。
学習の目的は学習データを正しく識別できる$w$を求めることで、学習データを1つずつ使って$w$を少しずつ修正していく方法などがある。
学習に使用しなかった**テストデータセット($D_T$)**で性能評価をする。
2.1.3. 教師付き学習と線形回帰
教師あり学習の回帰に関してです。Coursera機械学習入門オンライン講座の1週目 - 線形回帰と線形代数方がわかりやすく、内容としてそちらで十分です。
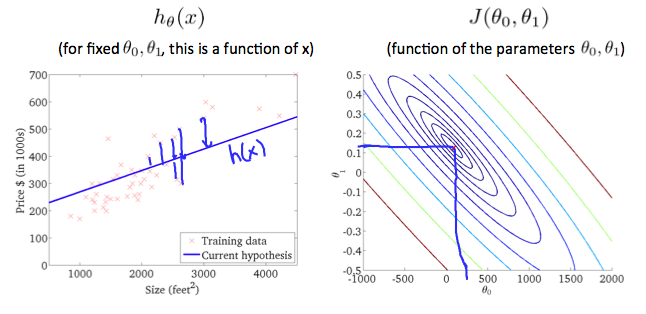
この本では、分類が主眼なので回帰に関しては割愛らしいです。
2.1.4. 教師なし学習
入力データ間の距離や類似度、統計的な性質に基づいて、クラスを自動的に生成(クラスタリング)する教師なし学習もある(自己組織型学習とも呼ぶ)。
一部のデータのみ教師をつけ、ほかは教師なしで学習を行う**形質導入学習(transductive learning)**という学習法もある。
記事「半教師あり学習_Semi-Supervised Learning」を見たほうが形質導入学習だけでなく、より大きな概念である「半教師あり学習」がわかりやすくまとまっています。
2.2. 汎化能力
(学習データではなく)未知のデータに対する識別能力を汎化能力といい、その誤差を汎化誤差という。
2.2.1. 学習データとテストデータの作り方
全データを教師データセット$D_L$とテストデータセット$D_T$に分割します。
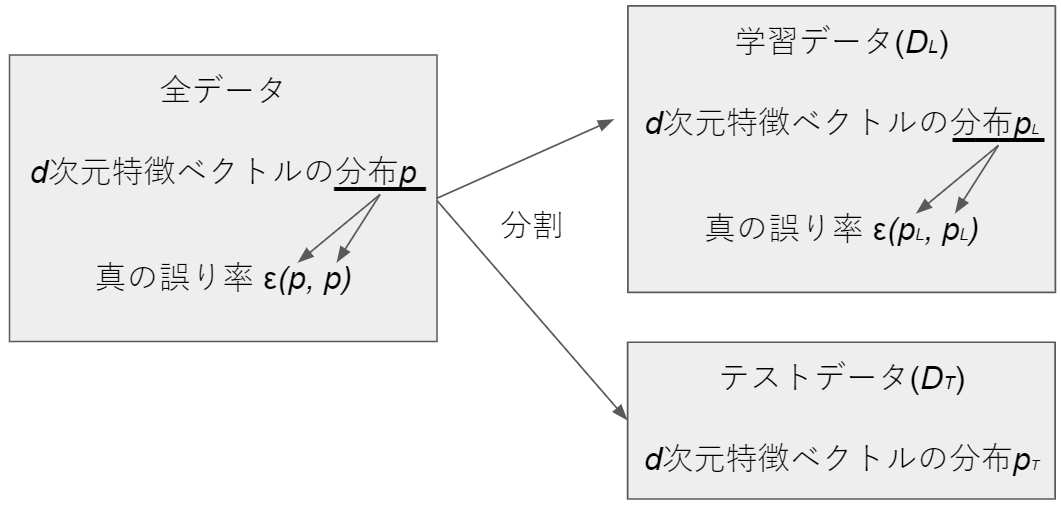
以下が用語です($\epsilon$は「イプシロン」と読みます)。
| 用語 | 説明 | 例 |
|---|---|---|
| 誤り率$\epsilon(p_L, p_T)$ | $D_L$で学習し$D_T$でテストしたときの誤り率 | 1万枚の硬貨のうち8000枚の学習データセットを使って学習し2000枚でテストしたときの誤り率 |
| 母集団 | すべてのデータ | 流通するすべての100円硬貨 |
| 真の分布($p$) | 母集団の$d$次元特徴分布 | 流通するすべての100円硬貨の分布 |
| 偏り(バイアス) | $D_L, D_T$の分布$p_L, p_T$と真の分布$p$とのずれ | 流通する100円硬貨全部と使用した1万枚の$D_L, D_T$の分布のずれ |
| 真の誤り率($\epsilon(p, p)$) | 真の分布$p$に従った学習データとテーストデータを使ったときの誤り率 | 流通する100円硬貨の分布でのモデルの誤り率 |
| 再代入誤り率($\epsilon(p_L, p_L)$) | 学習データでテストした場合の誤り率 | 8000枚の学習データセットを使って学習した場合の学習データの誤り率 |
以下が学習とテストにデータ分割する方法です。
(1) ホールドアウト法(holdout法)
データ全体を二分割し、一方を学習に使い($p_L$)と他方をテストに使う($p_T$)。このときの誤り率を**ホールドアウト誤り率(holdout error)**と呼び、$\epsilon(p_L, p_T)$で表す。
$再代入誤り率 \leq 真の誤り率 \leq ホールドアウト誤り率$ の関係が成り立つ。
E_{D_L}\{\epsilon(p_L, p_L)\} \leq \epsilon(p, p) \leq E_{D_T}\{\epsilon(p_L, p_T)\} \\
※ここでのEはExpectation(期待値)の頭文字
(2) 交差確認法(cross validation法)
交差確認法(cross validation法)は、交差検証法とも呼ばれデータをm個のグループに分割します。1グループをテストデータセット、その他を学習データセットとしm回学習とテストを実施。
例えば3分割($m=3$)にした場合は下記のとおりです。
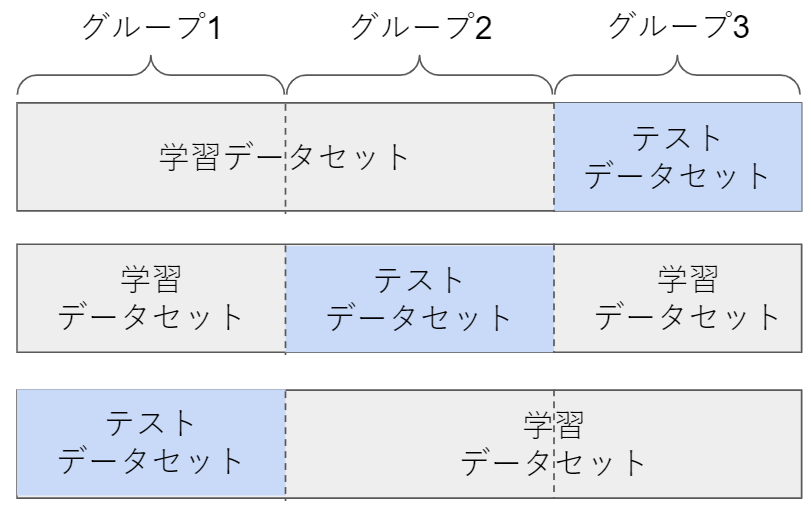
誤識別率の予測値は$i$番目のグループでテストしたときの誤り率を$\epsilon_{-1}$で表すと以下の通りです。
\epsilon = \frac{1}{m} \sum_{i=1}^m \epsilon_{-i}
(3) 一つ抜き法(leave-one-out法)
交差確認法の類似方法でジャックナイフ法とも呼ばれています。交差確認法はグループで分割しグループに対してテストをしていましたが、一つ抜き法では1件のデータだけをテスト用にして、1件以外のデータで学習をします。
データ数分だけ学習・テストを繰り返す(100件あったら100回学習とテストを実行する)ので時間がかかります。
(4) ブートストラップ法(bootstrap法)
N個のデータに対してN回の復元抽出をすることで、データN個のブートストラップサンプルを作る。
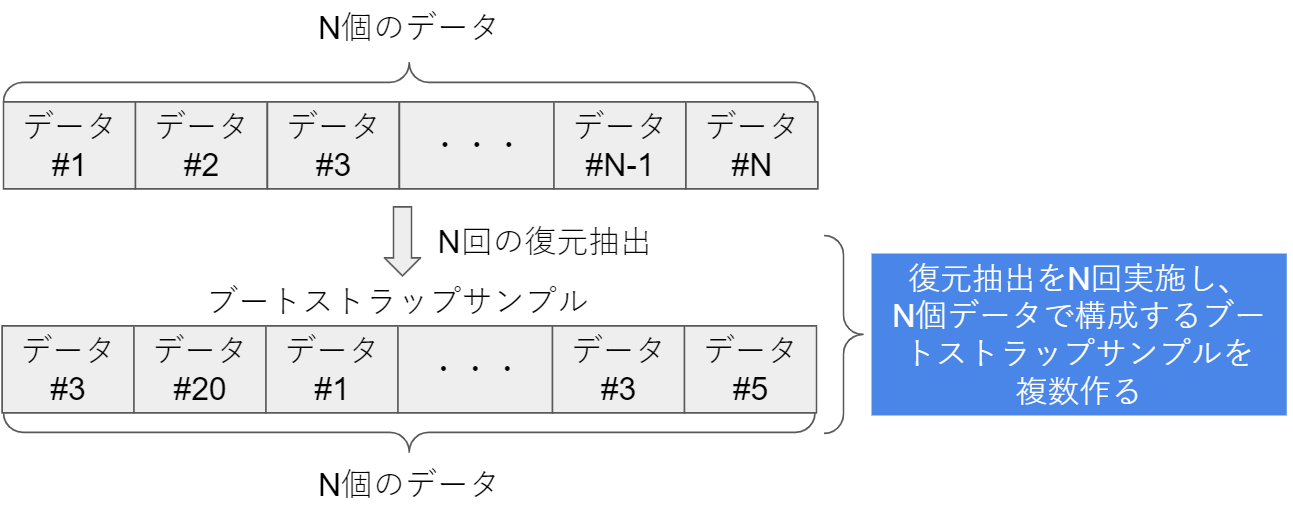
復元抽出は既に抽出されたデータも含めて抽出元とするため、データが重複する場合もある(上の図でいうブートストラップサンプルでのデータ#3が重複)。
ブートストラップサンプルから得られる誤識別率を$\epsilon(N^*,N^*)$と表し、もともとのデータ集合Nをテストデータとして得られるご識別率$\epsilon(N^*,N)$との差を求める。
bias = \epsilon(N^*,N^*) - \epsilon(N^*,N)
ブートストラップサンプルを複数(最低でも50程度らしい)生成し、上記の平均からバイアスを推定し、誤識別率の予測値$\epsilon$を求める。
※$\overline{bias}$はバイアスの平均。
\epsilon = \epsilon(N, N) - \overline{bias}
N回の復元抽出で1度サンプルされる確率$p'$
p' = 1-(1-\frac{1}{N})^N \approx 1-e^{-1} = 0.632
($1-\frac{1}{N})^N=e^{-1}$の部分を補足。
そもそもネイピア数$e$は$f(x)=a^x$の指数関数で$f'(0)=1$、つまり$x=0$の傾きが1となる底$a$の値。極限の計算式にすると以下の通り。
\lim_{h\rightarrow0}\frac{e^h-1}{h}=1
$h$を$x$にして。
\lim_{x\rightarrow0}\frac{e^x-1}{x}=1
さらに$e^x-1=u$とおくと$e^x=1+u$ , $x=\log{(1+u)}$となり、$x\rightarrow0$のとき$u\rightarrow0$となるので以下に変形(右辺は$=1$で固定)。
\lim_{x\rightarrow0}\frac{e^x-1}{x}=
\lim_{u\rightarrow0}\frac{u}{\log{(1+u)}}=
\lim_{u\rightarrow0}\frac{1}{\frac{\log{(1+u)}}{u}}=1
これから$\lim_{u\rightarrow0}\frac{\log{(1+u)}}{u}=1$となり、$u$を$x$に置き換え$\lim_{x\rightarrow0}\frac{\log{(1+x)}}{x}=1$が言える。$\frac{1}{x}$を前に出して右辺の$=1$の部分を$\log{e}$に変え、最後に$\log$を両辺とも取る。
\lim_{x\rightarrow0}\frac{1}{x}{\log{(1+x)}}=
\lim_{x\rightarrow0}{\log{(1+x)}}^\frac{1}{x}=\log{e} \\
\lim_{x\rightarrow0}{(1+x)}^\frac{1}{x}=1
さらに$x=\frac{1}{v}$に置き換えると$x\rightarrow0$のとき$v\rightarrow \pm \infty$となるので以下に変形。
\lim_{v\rightarrow\pm \infty}(1+\frac{1}{v})^v=e \\
\lim_{x\rightarrow\pm \infty}(1+\frac{1}{x})^x=e
あとは$x$を$-N$にすればはじパタに書かれている式になります!
※$N\rightarrow \pm \infty$は省略
(1-\frac{1}{N})^N \approx e^{-1}
P15脚注記載部分の計算式
\begin{eqnarray}
& &
(x+y)^n \\[5pt]
&=&
{}_n \mathrm{ C }_n x^n
+{}_n \mathrm{ C }_{n-1} x^{n-1} y
+{}_n \mathrm{ C }_{n-2} x^{n-2} y^2
+\cdots \\[5pt]
& & \cdots
+{}_n \mathrm{ C }_{k} x^k y^{n-k}
+\cdots
+{}_n \mathrm{ C }_1 x y^{n-1}
+{}_n \mathrm{ C }_0 y^n
\end{eqnarray}
上記を使って$x = 1$ $y=-\frac{1}{N}$として$(1-\frac{1}{N})^N$を展開します。これで脚注の左側の完成です。
(1-\frac{1}{N})^N =
{}_N \mathrm{ C }_{N} 1^N +
{}_N \mathrm{ C }_{N-1}1^{N-1}(-\frac{1}{N})^1 +
{}_N \mathrm{ C }_{N-2}1^{N-2}(-\frac{1}{N})^2 + \cdots \\
= 1 + N(-\frac{1}{N}) + \frac{N(N-1)}{2!} \frac{1}{N^2} - \cdots \\
この式はe^{-1}のマクローリン展開した式と同じです($N\rightarrow \pm \infty$にしているので同じ)。
e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\cdots \\
e^{-1}=1-1+\dfrac{1}{2!}-\dfrac{1}{3!}+\cdots
部分的に$\frac{N(N-1)}{2!}$を取り出して少し補足すると以下のように展開できます($N\rightarrow \pm \infty$の場合$\frac{1}{N}=0$なので)。
これで脚注部分もスッキリしました!
\lim_{N\rightarrow \pm \infty}\frac{N(N-1)}{2!} \frac{1}{N^2} =
\lim_{N\rightarrow \pm \infty}\frac{1-\frac{1}{N}}{2!} =
\frac{1}{2!}
以下は参考にしたリンクです。
簡単な手法比較
各手法の学習・テスト回数は以下の通り。
| 手法 | 学習・テスト回数 |
|---|---|
| ホールドアウト法 | 1回 |
| 交差確認法 | グループ数回 |
| 一つ抜き法 | データ数回 |
| ブートストラップ法 | 任意の数(50回程度以上と言われている)+1 "+1"は元データに対する学習・テスト |
Cross-Validation and Bootstrap for Accuracy Estimation and Model SelectionやComparing the Bootstrap and Cross-Validationに交差検証法とブートストラップ法の比較が書かれていて、非常に興味深い(チラ見程度だが、交差検証法の方が優れている?)。
2.2.2. 汎化能力の評価法とモデル選択
誤りが目標より小さくならない場合に識別関数を変える。識別関数を変えたりパラメータを変えたりする。テストデータに対する誤りが最も小さくなるパラメータを選択する方法をモデル選択という。
回帰(関数近似)の例だと、以下の式で考えることができる。
| 内容 | 式 | 備考 |
|---|---|---|
| サンプルデータ関数 | $f(x)=0.5+0.4*\sin(s \pi x) + \epsilon =$ $h(x)+\epsilon$ |
平均0、分散0.05の正規分布にノイズ $\epsilon$が乗った関数 |
| p次多項式による近似曲線 | $y(x;a)=a_0+a_1x+a_2x^2+\cdots+a_px^p$ $a=(a_0,a_1,\cdots,a_p)^T$ |
$y(x;a)$は特徴$x$を入力しパラメータ$a$を使った関数 |
| 平均自乗誤差(MSE: Mean Square Error) | $\int f(y(x;D)-h(x))^2 p(x) dx = $ $E\{ (y(x;D)-h(x))^2\}$ |
真実の関数と機械学習によりつくったモデル関数の結果との差の自乗 多項式パラメータ$a$は学習データセット$D$を決めると一意に決まるので$y(x;D)$としている $p(x)$は$p(x)=1$の確率密度関数 |
| 平均自乗誤差(複数データセット) | $MSE_D=E_D\{ (y(x;D)-h(x))^2\}$ | 機会学習の場合はデータセットに依存するため、データセットに対する値だということを明示 |
MSEに関しては、**バイアスと分散(バリアンス)**に分解できます。言葉の定義は下記のWikipedia参照。
バイアス(偏り)
学習アルゴリズムにおいて、誤差のうち、モデルの仮定の誤りに由来する分。バイアスが大きすぎることは、入力と出力の関係を適切に捉えられていないことを意味し、過少適合している。
バリアンス(分散)
誤差のうち、訓練データの揺らぎから生じる分。バリアンスが大きすぎることは、本来の出力ではなく、訓練データのランダムなノイズを学習していることを意味し、過剰適合している。
バイアスと分散はトレードオフの関係にあり、その関係をバイアス・分散トレードオフと呼びます。
バイアス・分散分解について
(y(x;D)-h(x))^2 = (y(x;D)-E_D{y(x;D)}+E_D{y(x;D)}-h(x))^2
式を展開していきます。
(y(x;D)-E_D\{y(x;D)\}+E_D\{y(x;D)\}-h(x))^2 = \\
(y(x;D)-E_D\{y(x;D)\})^2 +
(E_D\{y(x;D)\}-h(x))^2 + \\
2(y(x;D)-E_D\{y(x;D)\})(E_D\{y(x;D)\}-h(x))
$MSE_D=E_D\{ (y(x;D)-h(x))^2\}$のように実際は期待値をとっているので、最終項の$2(y(x;D)-E_D\{y(x;D)\})(E_D\{y(x;D)\}-h(x))$の部分はゼロになります。なぜなら最終項の前半部$(y(x;D)-E_D\{y(x;D)\})$が期待値をとるとゼロになるからです。
E_D\{(y(x;D)-E_D\{y(x;D)\})\} = E_D\{y(x;D)\}-E_D\{y(x;D)\} = 0
これで式が少し単純化できました。
MSE_D=E_D\{ (y(x;D)-h(x))^2\} \\
= (y(x;D)-E_D\{y(x;D)\})^2 + (E_D\{y(x;D)\}-h(x))^2
この前半部分$(E_D\{y(x;D)\}-h(x))^2$がバイアスで、モデルが予測する値と実際値との乖離です。
後半部分$(y(x;D)-E_D\{y(x;D)\})^2$がバリアンスで、データセットに依存するモデル間の分散です。
以下は理解する上で参考にしたリンク記事です。
- バイアス-バリアンス分解:機械学習の性能評価: バイアス - バリアンス分解について一番くわしい
- 機械学習のバイアスバリアンス分解を古典的な統計学から丁寧に解説する: 統計学も含めてバイアスバリアンス分解を解説
- 「統計的に有意」だけでは足りないワケ:バイアス-バリアンス分解のはなし: バイアスとバリアンスのイメージ図がわかりやすい
- バイアスとバリアンスを理解する: バイアスとバリアンスのPythonコードあり
- 条件付き期待値,分散の意味と有名公式: 条件付き期待値についての基本
※$\hat{a}$のように*^*が文字の上につくことを「ハット」と呼びます。推定値のこと。
「はじパタ」勉強系記事リンク
| 章 | 項目 | 時間(h) | 難易度 | 学んだこと |
|---|---|---|---|---|
| 1 | はじめに | 8.9 | 特徴の型, 特徴空間, 次元の呪い | |
| 2 | 識別規則と学習法の概要 | 12 | ホールドアウト法,交差確認法 ,一つ抜き法 ,ブートストラップ法 ,バイアス・分散トレードオフ, 過学習 | |
| 3 | ベイズの識別規則 | 14.8 | ベイズ識別規則, ROC曲線 | |
| 4 | 確率モデルと識別関数 | 18 |
|
平均ベクトル, 共分散行列, 標準化, 無相関化, 白色化, 正規分布, 最尤推定 |
| 5 | k最近傍法(kNN法) | 8 |
|
最近傍法, ボロノイ境界, kNN |
| 6 | 線形識別関数(前半) | 30.4 |
|
正規方程式 |
| 6 | 線形識別関数(後半) | 前半に時間は含む |
|
フィッシャーの線形判別関数, 判別分析法, ロジスティック回帰 |
| 7 | パーセプトロン型学習規則 | 13.5 |
|
多層パーセプトロン, 誤差逆伝播法, シグモイド関数 |
| 8 | サポートベクトルマシン | 14.7 |
|
カーネルトリック, ν-SVM |
| 9 | 部分空間法 | 15.4 |
|
主成分分析, 特異値分解, CLAFIC法, カーネル主成分分析, カーネル部分空間法 |
| 10 | クラスタリング | 8.4 |
|
距離の公理, ミンコフスキー距離, K-平均法, 融合法, 混合正規分布モデル |
| 11 | 識別機の組み合わせによる性能強化 | 11.6 |
|
ノーフリーランチ定理, 決定木, バギング, アダブースト, ランダムフォレスト |