バイアスとバリアンスを理解する

バイアスとバリアンス

前回は線形回帰について書いた。
ここでは、バイアスとバリアンスについて考える。
まず、学習の目的は、「観測不能な真の値と予測値との誤差を可能な限り小さくする」こと。観測不能な真の値を$y$、学習によって得られる解$\widehat{f}$とすると、

E_{ \widehat{f} } [(y-\widehat{f}(x)^{2}]

これを最小化することが学習の目的。
しかし、yを計算に組み込むことはできないので、下記のように変形する。

(E_{ \widehat{f} }[\widehat{f}(x)-f(x)])^{2}+ (E_{ \widehat{f} }[\widehat{f}(x)-E_{ \widehat{f}} [\widehat{f}(x)])^{2}]+ \sigma ^{2}

この変形式の導出は下記サイトが参考になる。
バイアス-バリアンス分解：機械学習の性能評価

第一項をバイアス、
第二項をバリアンス、
第三項をノイズ、
という。

バイアス

モデルと学習データの平均的なズレ。

(E_{ \widehat{f} }[\widehat{f}(x)-f(x)])^{2}

１．１．サンプルデータの作成

今回は、下記のような正弦関数にノイズを加えたデータを使用する。

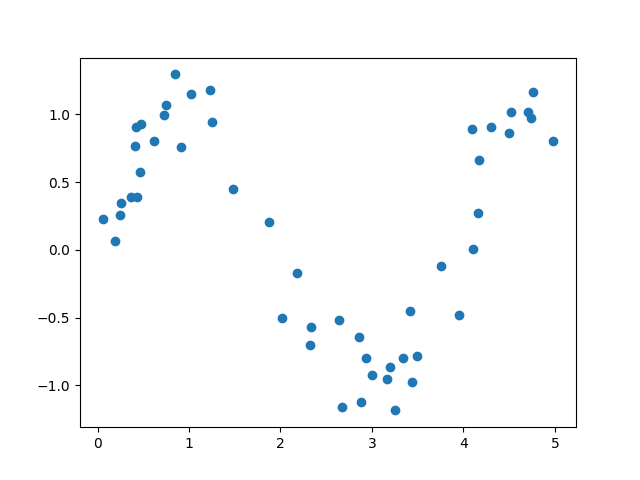
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
import math

np.random.seed(seed=32)
# create samples
sample_size = 50
noise_size = 0.2

dataX = np.linspace(0.0, 5.0, num=1000).reshape((1000, 1))
x = np.random.permutation(dataX)[:sample_size]
noise = noise_size * np.random.randn(sample_size, 1)
func = np.vectorize(math.sin)
y = func(x*1.6) + noise

１．２．モデルの作成

後で、モデル同士の精度を比べるため２つの多項式（３次元、９次元）を用意する。

dim = [3, 9]
for d in dim:
    poly = PolynomialFeatures(degree=d)
    X = poly.fit_transform(x)
    XTX = np.dot(X.T, X)
    XTX_inv = np.linalg.inv(XTX)
    a = np.dot(XTX_inv, np.dot(X.T, y))
    Xt = poly.fit_transform(dataX)
    yt = np.dot(Xt, a)
    plt.plot(dataX, yt, label='%d polynomial' % d)

今回も最小二乗法で最適なパラメータを求めた。
後、多項式モデルの生成はPolynomialFeaturesで作成した。
フィッテング結果は下図の通り。

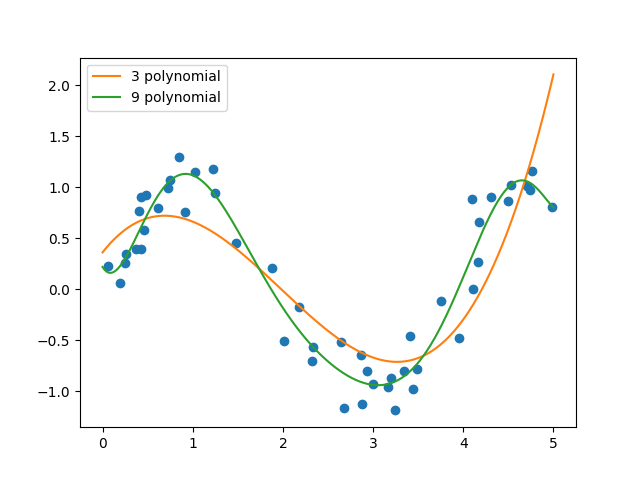
モデルを見る限り、９次元の多項式の方がよりフィットしているように見える。

１．３．誤差の計算

それぞれの平均二乗誤差を計算してみる。

for d in dim:
    # ...
    np.sum((y - np.dot(X, a)) ** 2)/sample_size

> polynomial3, 0.163705879935
> polynomial9, 0.0444546042927

９次元の多項式の方が誤差が小さいことが分かる。
この誤差のことを「バイアス」と言う。
バイアスは「関数（モデル）を複雑にするほど減少する」

バリアンス

バリアンスは、モデルの複雑さの度合い。
（モデルの分散と等価。）

(E_{ \widehat{f} }[\widehat{f}(x)]-E_{ \widehat{f}} [\widehat{f}(x)])^{2}]

２．１．バリアンスの計算

for d in dim:
    # ...
    np.var(np.dot(X, a))

> polynomial3, 0.437629402577
> polynomial9, 0.556897933262

３次元の方がバリアンスは小さい。
バリアンスは「関数（モデル）を複雑にするほど増加する」

→バイアスとバリアンスはトレードオフの関係

＊ノイズは、削除不能な誤差