この記事について
以下の観点から高次元空間の性質についてまとめます。
- 次元数と最近傍・最遠傍との距離の関係
- データ数と最近傍・最遠傍との距離の関係
- 人工データと実データの比較
はじめに
機械学習を使って何らかのタスクを解く上で、データの次元数は常に気にする必要があります。なぜなら、機械学習で扱う多くの問題はデータの次元数が大きくなるごとに難易度が跳ね上がるからです。
「次元の呪い」とも呼ばれるこの問題の原因は、高次元空間の性質にあると言われています。
データの次元数を大きくすると、私達の直感に反する興味深い挙動が確認できます。今回は、高次元空間の性質を簡単な数値実験で調べてみました。
次元の呪いとは
データの次元数が高次元になると、データが空間の外側に集中して分布する現象です。
高次元空間の直感的な理解のためには下記が参考になると思います。
確かにメロンパンの皮は、3次元空間では非常に薄っぺらなものでしかない。しかしそのメロンパンの皮の体積はn乗に比例して増加していくため、n次元空間では皮がメロンパンの大半を占めることになる。
超球をメロンパンに例えています。高次元空間においては、「皮」に相当する部分が体積の殆どを占めるようです。
3次元では皮の体積が3%であるのに対し、500次元では99.3%が皮になります。とても不思議です。
空間上に分布するデータに関しては、Wikipediaの数式が理解の助けになります。
\lim_{d \to \infty} E\left[ \frac{\mathrm{dist}_\mathrm{max}(d) - \mathrm{dist}_\mathrm{min}(d)}{\mathrm{dist}_\mathrm{min}(d)} \right] \to 0
次元数の増加に伴い、任意の点からの最近傍点と最遠傍点との差が0に近づくそうです。やっぱり不思議です。
この性質は、数値実験で確認することができます。
実験
データの次元数について実験を行いました。こちらコードをほぼそのまま使っています。
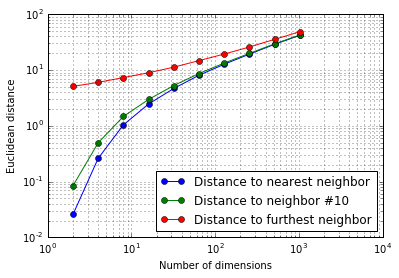
次元数と最近傍・最遠傍との距離の関係
$d$次元標準正規乱数を10000点生成します。10000点からランダムにサンプリングした40点について、最近傍、10番目の近傍、最遠傍点との距離を計算しました。
| 設定 | 値 |
|---|---|
| データ数 | 10000 |
| 次元数 | 2,4,8,16,32,64,128,256,512,1024 |
| 距離 | ユークリッド距離 |
次元数の増加とともに、最近傍、10番目の近傍、最遠傍との距離の差が小さくなっていることが確認できます。
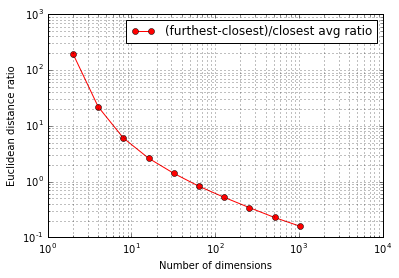
先ほどの式の挙動もプロットしてみます。
0に近づいていくことがわかります。すなわち、高次元空間では近傍と遠傍の差がほとんどないことになります。
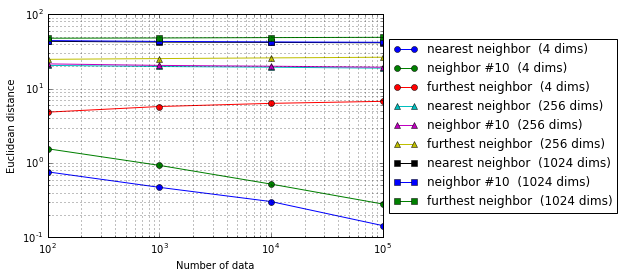
データ数と最近傍・最遠傍との距離の関係
高次元空間でも一定のデータ数を確保することで呪いを軽減できないでしょうか。「次元の呪い」はデータ数で克服できるのか検証してみます。
設定は前の実験とほぼ同じで、データ数を可変にします。
| 設定 | 値 |
|---|---|
| データ数 | 100,1000,10000,100000 |
| 次元数 | 4,256,1024 |
| 距離 | ユークリッド距離 |
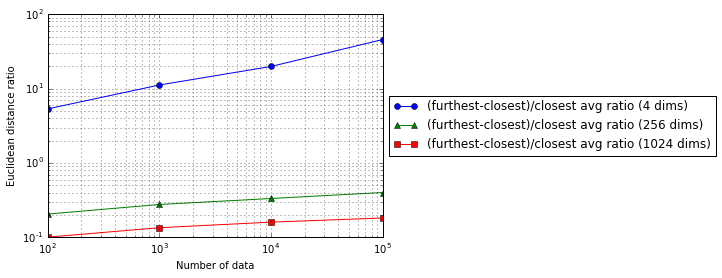
4次元の場合と比べて、256次元や1024次元の変化はごくわずかです。データ数を増やしてもほとんど効果が無いことがわかりました。
呪いに対してデータ数を増やすことはあまり有効ではないようです。次元削減を検討したほうが良いかもしれません。
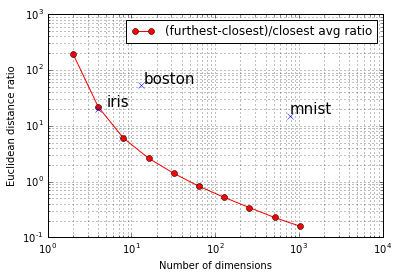
人工データと実データの比較
ここまでの実験はすべて人工データによる実験でした。最後に、現実のデータの振る舞いも見ておきます。ここでは実データとして、ベンチマークによく用いられるデータセットをいくつか用意しました。
| 設定 | 値 |
|---|---|
| データセット | iris(アヤメの大きさ),boston(ボストンの家の値段),mnist(手書き文字) |
| 次元数 | それぞれ、4,13,784 |
| 距離 | ユークリッド距離 |
実データは人工データよりもきれいに分布していないのか、次元数の割には最近傍と最遠傍の距離は小さくないようです。現実のデータは価値のない変数を含んでいることがよくあるので、潜在的な次元数は見かけの次元数より小さくなります。
このグラフからは言い切れませんが、ベンチマークとしてよく使われるデータセットは、赤線よりも右上に分布するものが多いそうです。
余談ですが、irisとmnistの差がほとんどありません。この実験だけでは断言できませんが、mnistは次元数の割には易しいデータセットなのかもしれませんね。
まとめ
いくつかの数値実験を通して高次元空間とデータの性質について調べました。
高次元空間では近傍と遠傍の差が小さくなる傾向にあること、データ数を増やしても高次元データは扱いやすくならないことが確認できました。