はじパタ9章で飛ばされがちな部分の説明2(特異値分解、CLAFIC法)

はじパタ9章をそこそこ頑張って読んでもわからなかった人を対象にしています。
(社内勉強会用なので、言葉足らずな部分があるかも。。コメントしていただけたらできるだけすぐ返事します)
行列の四則演算、転置行列の定義や展開方法、行列の微分、逆行列は知っている前提です。

部分空間、グラム-シュミットの正規直交化, 主成分分析に関する説明はこちら↓
http://qiita.com/kaityo256/items/48de63526b469235d16a

行列の四則演算、転置行列の定義や展開方法、行列の微分、逆行列に詳しくない人へ

• 行列の足し算、引き算
• 行列の掛け算
• 転置行列、逆行列、対称行列について
• 行列の微分について(各成分に対して偏微分しているだけ)

特異値分解

はじパタで出てきた計算式が分かりやすかったと思うので、これも補足説明ぐらいにとどめておきます。

はじパタのこの部分で計算式で抑えとかないといけない知識としては直交行列Aの転置行列はAの逆行列と一致する(定義として)とか逆行列、単位行列の定義ぐらいでしょうか。

「ランクqの誤差最小という意味での最良近似」とは

私のように数学に疎いと直感的に「ランクqの最良近似ってq次元への主成分分析とちゃうん？」と思ってしまいますが、これは全く違います。
実際に適当な行列で試してみるとわかりますが、特異値分解をしてΛqで近似しても元の学習データXの次元は変わりません。

それよりも、低ランクに近似することで機械学習の分野で言うと過学習を防ぐ効果があるようです。
数学的に言うと(多分)「同じ性質だけど別のベクトルで表されているものを(ほぼ)同じベクトルで表現し直す」という感じでしょうか。(高校生の時に行列を使って連立方程式を解いたことのある人はこの表現でピンとくるかもしれない・・・)

具体例としては個人的にはこの説明がしっくり来ました。
この説明だと、

1. このままだと「車」と「自動車」を全く違う単語をとしてみなされる。
2. でも「会場に車で行く」と「会場に自動車で行く」など、「車」と「自動車」が全く同じ使われ方をしていたら、低ランクに近似するだけで「車」と「自動車」がほぼ同じ単語だということを計算できる。

ということが特異値分解を使うと出来るようになります。
実際にここのサンプルコードを使って低ランクへの近似をしてみると違いがわかります。

近似前

       d1   d2   d3   d4
会場    1    1    1    0
店      0    0    0    1
自動車  0    1    0    0
自転車  0    0    1    1
行く    1    1    1    1
車      1    0    0    0

近似後

       d1             d2            d3          d4
会場    0.78981446  0.78981446  0.88310812  0.65972974
店      0.21157926  0.21157926  0.23657121  0.17673155
自動車  0.25329821  0.25329821  0.28321804  0.21157926
自転車  0.4947973   0.4947973   0.55324325  0.41330276
行く    1.00139372  1.00139372  1.11967933  0.83646129
車      0.25329821  0.25329821  0.28321804  0.21157926

このように、近似前だと

自動車の単語ベクトル: [0, 1, 0, 0]
車の単語ベクトル: [1, 0, 0, 0]

と全然違いますが、近似後は

自動車の単語ベクトル: [0.25329821, 0.25329821, 0.28321804, 0.21157926]
車の単語ベクトル: [0.25329821, 0.25329821, 0.28321804, 0.21157926]

と一致します。

なぜ特異値分解による近似が「誤差最小という意味での最良近似」なのか

TODO: そのうち書きます。

CLAFIC法

用語解説

• 正射影とは

CLAFIC法の手順

1. 学習データ(教師ありデータ)をもとに、各クラス(C1 ... Ck)の部分空間(S1 ... Sk)の基底ベクトルをもとめる(後述詳細)
2. 基底ベクトルが定まると判別するためのデータを各部分空間に正射影することができるので、正射影して、正射影後のベクトルの長さが一番長い部分空間のクラスに判別する。

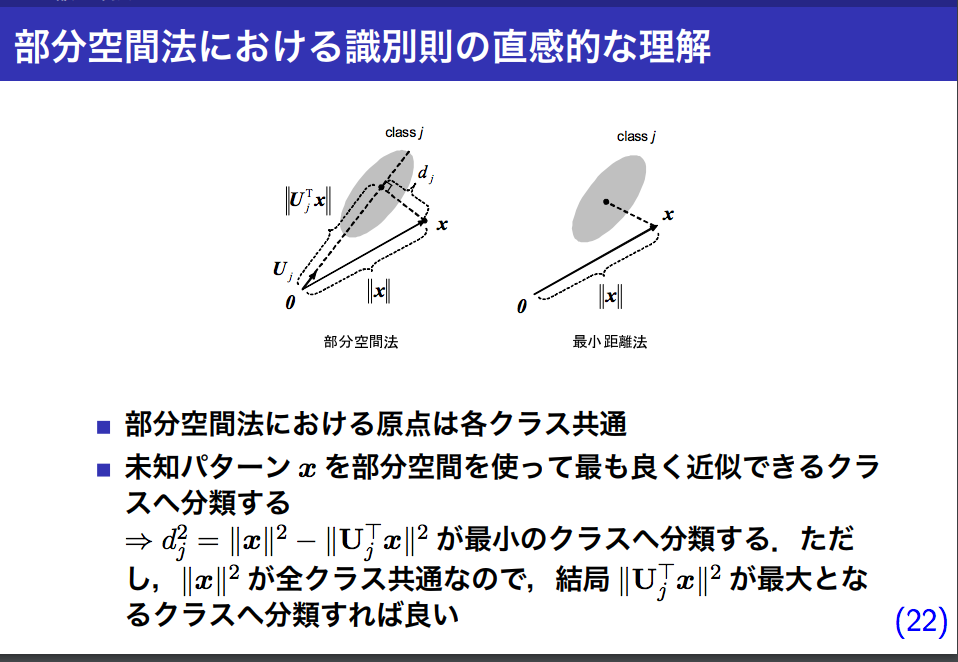
なぜ「正射影後のベクトルの長さが長いほうが良い」みたいになっているのか

下の図の説明が一番しっくり来た

http://web.tuat.ac.jp/~s-hotta/RSJ2012/RSJ2012_hotta.pdf
より抜粋

正射影後のベクトルは元のベクトルよりも低次元になるせいで絶対長さは短くなる。
その中でも一番長いベクトルは、元のベクトルを一番良く近似できている、ということになるので、「正射影後のベクトルの長さが一番長いベクトルのクラスに判別する」ということになる。

学習データをもとに、各クラスの部分空間の基底ベクトルを求める方法

上の説明通り、
「クラスCiの学習データ群を基底ベクトルで正射影したときのベクトルの長さの期待値を最大化するような基底ベクトル」(=クラスCiの学習データ群をよく近似できている基底ベクトル)を求めることになる。
(学習データは何個もあるので長さの期待値を指標とする)
また、はじパタで ||uij|| = 1 と書いてあるように、正規基底ベクトルを求めることになる。(計算しやすいから？)

正射影の定義に沿うと、ベクトルxを基底ベクトルの一つであるuijで正射影した後のベクトルは

\frac{\vec{u_{ij}}・\vec{x}}{|\vec{u_{ij}}|^2}\vec{u_{ij}}

となる
||uij|| = 1であることを適用すると、このベクトルの長さは

\vec{u_{ij}}・\vec{x}

また、ベクトルの内積の代数的意味と行列の積の定義を元に計算すると、

\vec{u_{ij}}・\vec{x} = \vec{x}^T\vec{u_{ij}} = \vec{u_{ij}}^T\vec{x}

(式１)が成り立つ。

よって、ベクトルxを基底ベクトルの全体(ui1, ... , uidi)で正射影した後のベクトルの長さは(ベクトルの長さの定義より)

\sqrt{\sum^{d_i}_{j=1}(\vec{u_{ij}}・\vec{x})^2}
= \sqrt{\sum^{d_i}_{j=1}(\vec{x}^T\vec{u_{ij}})^2}
= \sqrt{\sum^{d_i}_{j=1}(\vec{u_{ij}}^T\vec{x})^2}

となる。よってこれをxだけでなく、クラスCiに含まれている学習データすべての正射影後のベクトルの長さの平均(=期待値)を

E\{\sqrt{\sum^{d_i}_{j=1}(\vec{x}^T\vec{u_{ij}})^2}\}

と置くと、これを最大化するuij, ... uidiが、クラスCiの基底ベクトルとなる。
√を取っても大小関係は変わらないので、

E\{\sum^{d_i}_{j=1}(\vec{x}^T\vec{u_{ij}})^2\}

を最大化することとする。また期待値は学習データ(x)にのみ関係することで、uij, j, di には全く関係ないので

E\{\sum^{d_i}_{j=1}(\vec{x}^T\vec{u_{ij}})^2\}
= \sum^{d_i}_{j=1}E\{(\vec{x}^T\vec{u_{ij}})^2\}

とおける。これを||uij|| = 1という制約のもと最大化するuijを見つけるためにラグランジュの未定乗数法を用いると

L_i(u_{ij}) = \sum^{d_i}_{j=1}E\{(\vec{x}^T\vec{u_{ij}})^2\} - \sum^{d_i}_{j=1}λ(\vec{u_{ij}}^T\vec{u_{ij}} - 1)

というラグランジュ関数(はじパタ145ページの下にあるやつ)が得られる。
上の(式1)を用いて

\vec{x}^T\vec{u_{ij}} = \vec{u_{ij}}^T\vec{x}

をLiに代入して展開して、ラグランジュの未定乗数法にもとづいて解いていくと(ここははじパタの146ページの上の途中式参照)

E\{\vec{x}\vec{x}^T|\vec{x} \in{C_i}\}\vec{u_{ij}} = λ_{ij}\vec{u_{ij}}\\

E\{\vec{x}\vec{x}^T|\vec{x} \in{C_i}\} := \vec{x}の自己相関行列。はじパタではQ_iとして表されている

という固有値問題が得られる。
あとはこれを解いて固有ベクトルを得られれば、それがクラスCiの部分空間の基底ベクトルとなる。
(ただしはじパタに書いてある「忠実度」によって部分空間の次元数に制限を設ける)

CLAFIC法の実装

軽く調べてもライブラリがなかったので、 ここに
CLAFIC法でirisデータを分類するためのサンプルコードを書いておきました。

前間違って消しました。。

参考にしたサイト

非常に分かりやすかったです。本当にありがとうございました。

• http://www24.atpages.jp/venvenkazuya/mathC/matrix3.php
• http://www.geisya.or.jp/~mwm48961/kou2/matrix2.html
• http://www.geisya.or.jp/~mwm48961/linear_algebra/transpose1.htm
• http://yusuke-ujitoko.hatenablog.com/entry/2017/05/04/000401
• https://abicky.net/2012/03/24/211818/
• http://qiita.com/Hiroki11x/items/99a3ddd201b1d0e4645f
• http://web.tuat.ac.jp/~s-hotta/RSJ2012/RSJ2012_hotta.pdf
• http://mathtrain.jp
• http://www.geisya.or.jp/~mwm48961/kou2/v_coord4.html