フィッシャーの線形判別分析法

はじめに

　学校課題のついでに，線形判別分析（Linear Discriminant Analysis, LDA）の有名なアルゴリズムであるFisherの線形判別について書いてみました．分かりにくい部分もあると思いますが，ご容赦ください．

線形判別分析

　線形判別分析とは2つのクラスを"最もよく判別できる"直線を求める手法です．
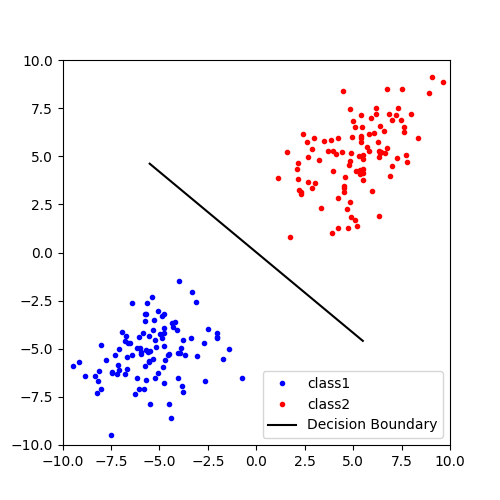
　データが直線のどちら側にあるかを見ることで，どちらのクラスに属するか判別することができます．この直線のことを決定境界と言います．わかりやすいように各クラスに属するデータは2次元のデータであるとすると，決定境界は下図のようなイメージです．

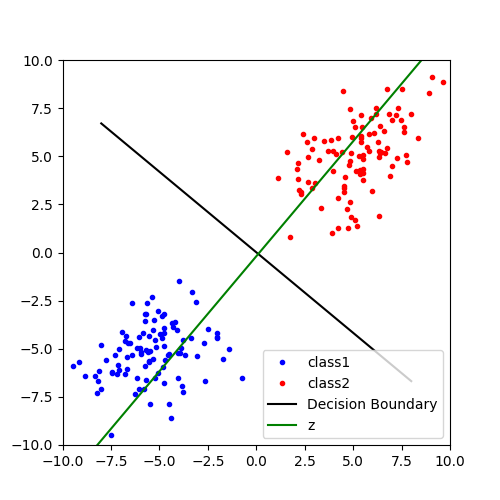
　「直線のどちら側にあるかを見る」と言いましたが，実際にデータを識別するときは適当な線形変換によってデータを直線z上に写像すると2つのクラスを判別しやすいと思います．データを1次元に圧縮すれば，閾値となるスカラー値を適当に設定してどちらのクラスに属するのか判別できますね．フィッシャーの線形判別分析は，この射影先の直線zを見つけるための手法の1つです．
　

　さて，この線形変換を行列式で表すと，

y_n = w^T x_n

となります．x_nはD次元のデータ，wが線形変換ベクトル（x_nと同じD次元のベクトル），y_nは線形変換された1次元データ（スカラー）です．

　ちなみに線形判別分析は，判別対象が2クラスではなく多クラスになっても対応可能です．
　また，各クラスのデータが2次元ではなく3次元以上でも適応できます．この場合の決定境界は直線ではなく平面や超平面になります．

フィッシャーの線形判別分析の導出

　実際にデータを見ながらフィッシャーの線形判別の導出をやってみます．フィッシャーの線形判別は，射影した各クラスの分離度が最も大きくなるような線形変換ベクトルw（データを射影する直線zの傾きになる）を見つけるという手法になります．

　まず，以下のようなデータC₁とC₂を考えます．

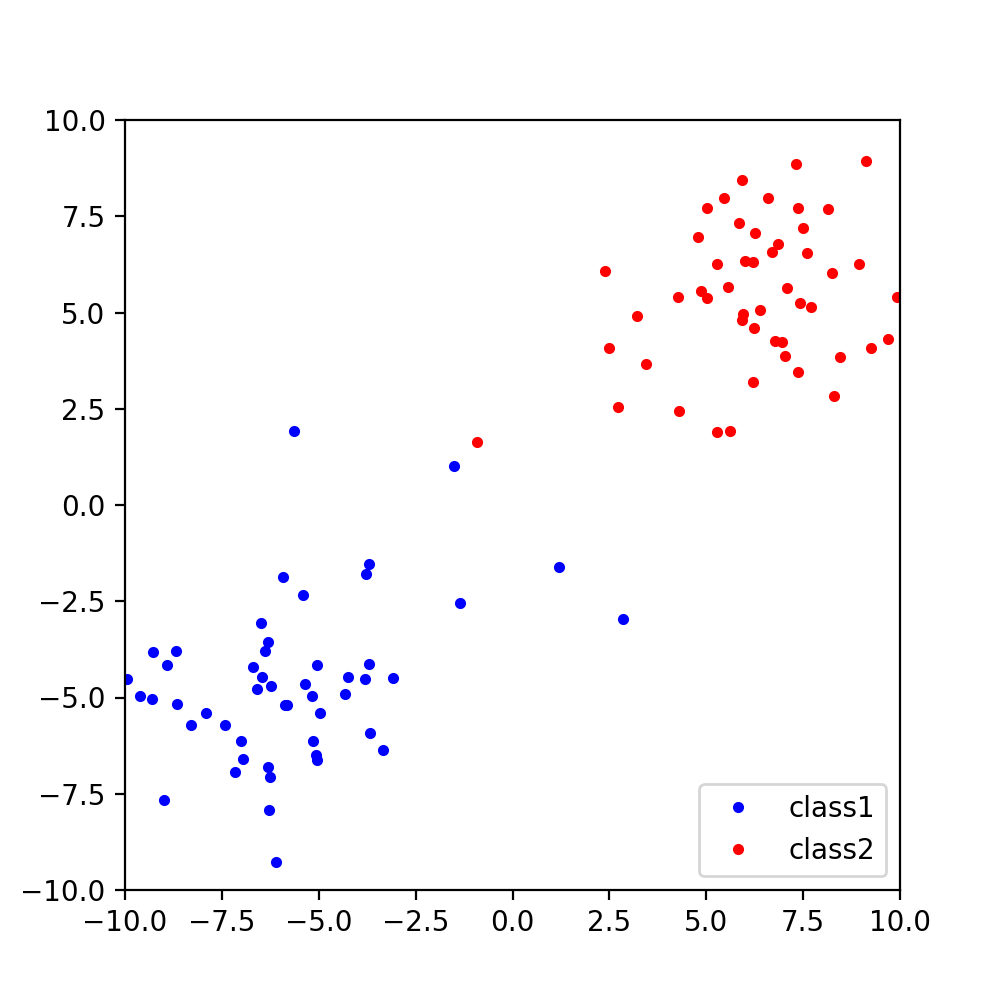
　クラスC_kのデータ数をN_kとすると，各クラスの平均は，

m_1 = \frac{1}{N_1}\sum_{n \in C_1}x_n

m_2 = \frac{1}{N_2}\sum_{n \in C_2}x_n

となります．このm₁とm₂を各クラスの代表点として，この2点が線形変換ベクトルwによって射影されたときに最も離れるようにします．つまり，

w^T m_1 - w^T m_2 = w^T (m_1 - m_2)

が最大になるようにwを決定します．ただし，必要なのは最大値を与えるベクトルwの傾きなのでベクトルw自体の大きさを大きくしても意味がありません．したがって，wは単位長であるという制約

|w|=1

を与えて，ラグランジュの未定乗数法で最大値を求めると

w \propto (m_1 - m_2)

となります．これは，wが各クラスの平均値を結ぶ線分と平行になるということを意味しています．実際にこのベクトルwから決定境界の直線を引いてみます．決定境界の直線はwに直交し，各クラスの平均を結ぶ線分の中点を通る直線になっているので以下の図のようになります．

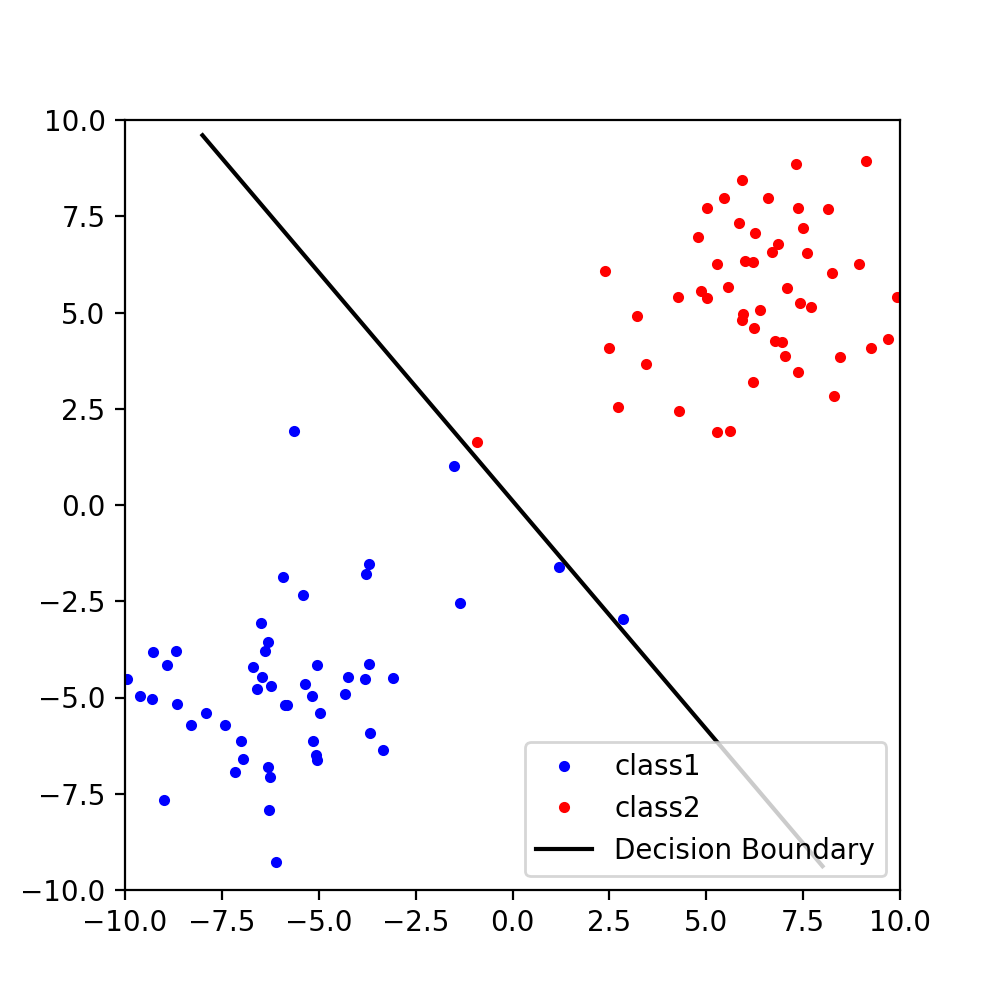
C₁の青い点が決定境界の直線の上にもあります．これだけでは上手く判別することができませんでした．

---

　実は，各クラスの平均値だけを見ていると上手く判別することができません．例えば，C₁の青い点がC₂の赤い点が密集している位置に混ざっていても，一方でC₂から遠く離れた位置にたくさんの青い点が存在すれば，平均的には2つのクラスは離れているとみなされてしまうからです．つまり，各クラスの点のばらつきが大きいと，平均的な位置が離れていても適切な決定境界を引くことができないということです．

　ここでベクトルwの決定のためにもう1つ条件を加えます．それは，同じクラス内のデータは射影した後でなるべく近くに密集してほしいというものです．つまり，射影後の各クラス内の分散を小さくするということです．射影後の各クラスの分散を数式で表すと，

s_1^2 = \sum_{n \in C_1} (w^T x_n - w^T m_1)^2

s_2^2 = \sum_{n \in C_2} (w^T x_n - w^T m_2)^2

となります．したがって，各クラス内の分散を小さくするためには，

s^2 = s_1^2 + s_2^2

を最小化すれば良いということです．

---

適切なwを見つけるためには，

1. 線形変換した2つのクラスがなるべく離れるように，各クラス間の平均の差がなるべく大きくなるようにする．
2. 線形変換した各クラス内のデータがなるべく密集するように，各クラス内の分散がなるべく小さくなるようにする．

の2つの条件が必要なことがわかりました．この2つの条件は，分数を用いて1つの条件として扱うことができます．つまり，

J(w) = \frac{(クラス間の平均に関する最大化問題)}{(クラス内の分散に関する最小化問題)}

という式にして，評価関数J(w)を最大化すれば良いということです．

　ただし，分子と分母を同様に扱うために，分子も平均ではなく分散の形で表します.
つまり分子を，

w^T (m_1 -m_2)

から

w^T (m_1 - m_2) (m_1 - m_2)^T w

という形式にします．このとき，

S_B = (m_1 - m_2) (m_1 - m_2)^T

をクラス間共分散行列と呼びます．

したがって，分子は

w^T S_B w

と書くことができます．

　また，分母は，

s^2 = s_1^2 + s_2^2 = \sum_{n \in C_1} (w^T x_n - w^T m_1)^2 + \sum_{n \in C_2} (w^T x_n - w^T m_2)^2

でしたが，

S_W = \sum_{n \in C_1} (x_n - m_1)^2 + \sum_{n \in C_2} (x_n - m_2)^2

とおくと，

s^2 = w^T S_W w

と書くことができます．このときS_Wを総クラス内共分散行列と呼びます．

　したがって，評価関数J(w)は，

J(w) = \frac{w^T S_B w}{w^T S_W w}

と表現することができて，これを最大化するwを求めます．ラグランジュの未定乗数法で解くと最終的に，

w \propto {S_W}^{-1} S_B w \propto {S_W}^{-1} (m_1 - m_2)

　となります．

　結論は，D次元のデータから各クラス内の平均と総クラス内共分散行列の逆行列を求めれば線形変換ベクトルwが求まり，決定境界が定まるということです．

実際にやってみると，良い感じに決定境界の直線を引くことができました．

---

適当にデータを生成して，フィッシャーの線形判別で決定境界を引くプログラムを書いてみる．

fisher.py

#coding: utf-8

import numpy as np
import matplotlib.pyplot as plt

DIM = 2 #データの次元数

#直線の式
def f(x, a, b):
	return a*x+b

#図示
def plot(cls1, cls2, line=None):
	x,y = cls1.T
	plt.plot(x, y, 'bo', ms=3, label='class1')
	x, y = cls2.T
	plt.plot(x, y, 'ro', ms=3, label='class2')

	if not (line is None):
		plt.plot(line[0], line[1], 'k-', ms=5)

	plt.xlim(-10,10)
	plt.ylim(-10,10)

	plt.show()

def fisher(cls1, cls2):
	#リストからnp.arrayに変換（行列の転置や逆行列を扱うため）
	cls1 = np.array(cls1)
	cls2 = np.array(cls2)

	#各クラスの平均値
	mean1 = np.mean(cls1, axis=0)
	mean2 = np.mean(cls2, axis=0)

	#総クラス内共分散行列
	sw = np.zeros((DIM,DIM))
	for xn in cls1:
		xn = xn.reshape(DIM,1)
		mean1 = mean1.reshape(DIM,1)
		sw += np.dot((xn-mean1),(xn-mean1).T)
	for xn in cls2:
		xn = xn.reshape(DIM,1)
		mean2 = mean2.reshape(DIM,1)
		sw += np.dot((xn-mean2),(xn-mean2).T)

	#総クラス内共分散行列の逆行列
	sw_inv = np.linalg.inv(sw)

	#wを求める
	w = np.dot(sw_inv,(mean1-mean2))

	#決定境界直線を図示する
	mean = (mean1 + mean2)/2 #平均値の中点
	a = -w[0]/w[1] #wと直交する
	b = a*mean[0]+mean[1]
	x = np.linspace(-8, 8, 1000)
	y = f(x,a,b)

	plot(cls1, cls2, (x,y))
	
	return w

if __name__ == '__main__':
	#テスト用2次元データ
	cov = [[3,1],[1,3]] #共分散
	cls1 = np.random.multivariate_normal([-5,-5], cov, 50)
	cls2 = np.random.multivariate_normal([5,5], cov, 50)

	#fisherで線形変換ベクトルwを求める
	w = fisher(cls1, cls2)
	print('w =', w, '\n')

実行結果

良い感じの決定境界の直線が引けてますね．

おわりに

　Fisherの線形判別分析をやってみました．他の手法との識別精度の比較をしてみたいですね．

参考

• フィッシャーの線形判別
• フィッシャーの線形判別
• 線形識別器 - Fisherの線形判別関数，単純パーセプトロン，IRLS