この記事は 学生団体 P&D Advent Calendar 2017 2日目の投稿です.
担当は前日の後輩から謎のプレッシャーをかけられた3000万です.
全力投球で頑張ります.
はじめに
最近P&Dで機械学習やデータ分析に興味もってそうな人がチラホラ見られたので,自分の勉強も兼ねてとっかかりやすい決定木の話を調べてなるべく丁寧にまとめようと思います.
と言っても厳密な数学で話を進めていませんし,機械学習やデータ分析について素人に近いので間違いがありましたらコメントお願いします.
決定木(Decision Tree)
決定木とは木構造を用いて分類や回帰を行う機械学習の手法の一つです.
分類木と回帰木の総称して決定木といいます.
名前の通り分類木は対象を分類する問題を解き,回帰木は対象の数値を推定する問題を解きます.
文字だとわかりにくいので以下に具体例を示します.
(以下の例と図はこちらのページが直観的に理解しやすかったので引用させて頂きました.)
※分類木および回帰木の一番最後の図、直線の引き方が微妙に違いますので注意してください!(コメント欄参照)
分類木(Classification Tree)
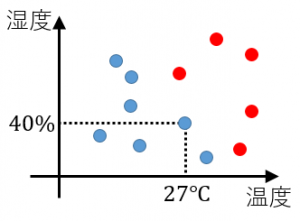
日々の温度と湿度のデータ,その日Aさんが暑いと感じたか暑くないと感じたかかのデータが与えられた状況を考えます.
赤い点が暑いと感じた日,青い点が暑くないと感じた日です.
例えば温度が27度で湿度が40%の日は暑くないと感じています.
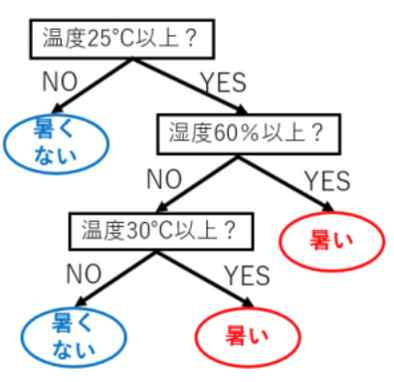
このデータから「温度と湿度がどのようなときにどう感じるのか?」といったことを木で表現できます.
この木のことを__分類木__といいます.
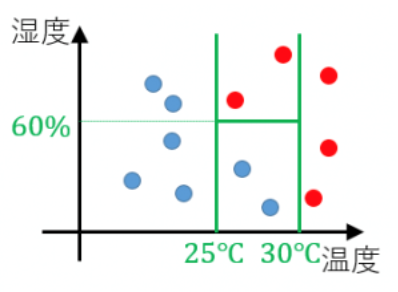
この木をさきほどのグラフに描画するとこのようになります.
以上が,Aさんがその日の温度と湿度によって暑いと感じるか否かを分類するモデルです.
回帰木(Regression Tree)
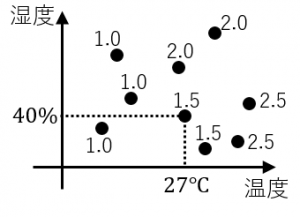
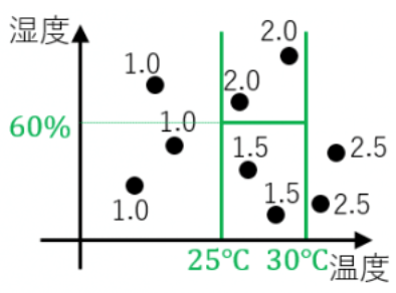
日々の温度と湿度のデータ.その日Aさんが飲んだ水の量のデータが与えらえれた状況を考えます.
例えば温度が27度で湿度が40%の日は水を1.5L飲んでいます.
分類木のときと同様にこのデータから「温度と湿度がどのようなときに水を何L飲むか?」といったことを木で表現できます.
この木のことを__回帰木__といいます.
この図を同様にグラフに描画するとこのようになります.
以上が,Aさんがその日の温度と湿度によって水を何L飲むのかを推定するモデルです.
決定木の特徴(?)
- 「決定木」はアルゴリズムの名前ではない
アルゴリズムはID3やC4.5,CARTと様々あります.
- ノンパラメトリックな教師あり学習の手法
解析対象のデータの分布を仮定しません.
また,事前に与えられたデータから未知のデータについて推定を行います.
- 結構使われている
Data Miningで使われるアルゴリズムTop10に2つランクインするくらいメジャーだそうです.
(少し古いですがソースはこちら)
決定木の長所と短所
次に決定木の長所と短所についてまとめていきます.
長所
- 可読性が高い
木が生成されるイメージからして出力結果の分析が容易そうですね.
- 説明変数・目的変数共に名義尺度から間隔尺度まで様々扱える
質的データから量的データまで様々扱えます.
- 外れ値に対して頑健
短所
- 分類性能の高い手法ではない
やはりSVMなんかが強い.
- 過学習を起こしやすい
パラメータの調整や枝の刈り込みを上手に行う必要があります.
- 線形性のあるデータには適していない
回帰モデルを使いましょう.
- XORなど多変数を考慮した分類はできない
多変数の状態を表現できれば...
決定木の構築(イメージ)
次はいよいよ決定木の構築についてです.
以下の図は自分で作ったもので赤丸と緑丸を分類する2値分類の例です.

まず,構築のために学習データが全てルートノードに集められます.
そこで,そのデータの持つ素性の中で集められたデータを一番よく分割する素性と閾値の組を選びます.
その素性と閾値で分割後,またそれぞれのノードで分割を繰り返し行っていきます.
この手順で決定木は構築されていきます.
で,この「一番よく分割する素性と閾値の組を選ぶ」というところが肝になってきます.
言い換えると__ノード内の不純度を最大限減らす素性と閾値の組を選ぶ__ということです.
どのようにしてそれらの組を決めるのでしょうか?
この組を選び出すのによく使われているのが__エントロピー__と__ジニ不純度__です.
これらの話を数式を交えて(アレルギーな方にも可能な限りわかりやすく)説明したいと思います.
エントロピーの意味とC4.5
エントロピーとは物事の乱雑さを測る指標のことで,情報系の方には情報量あたりのお話でお馴染みかと思います.
以下のような式で表現ができます.
I_H(t) = - \sum_{i = 1}^{c} p(i|t)log_2 p(i|t) \\
ただし,p(i|t) = \frac{n_i}{N} \\
cは目的変数のクラス数,tは現在のノード,Nはトレーニングデータのサンプル数,niはクラスiに属するトレーニングデータの数を示しています.
例えば以下のようなノードtについて考えると,クラス数が3,サンプル数が9,赤のサンプル数が3,青のサンプル数が2,緑のサンプル数が4といった対応になっています.
これで,数字を当てはめるだけで任意のノードについてエントロピーは簡単に求めることがわかりました.
では,このエントロピーとノードの不純度にどのような関係があるのかを見ていきたいと思います.
ノードの不純度が最も低い場合と高い場合について考えてみます.
ノードの不純度が最も低い,言い換えるとノード内のサンプルが全て同じクラスに属しているということです.
(先ほどのノードの例で言うと全てのサンプルが赤色であるようなケース)
この状態のノードに対してエントロピーを計算してみると
I_H(t) = - \sum_{i = 1}^{1} \frac{n_i}{N} log_2 \frac{n_i}{N} = \frac{N}{N} log_2 \frac{N}{N} = 0
といった結果になるかと思います.
同様にノードの不純度が最も高い,すなわちノード内のサンプルが全て異なるクラスに属しているということです.
(先ほどのノードの例でいうと全てのサンプルが別の色であるようなケース)
その状態のノードに対してエントロピーを計算してみると
I_H(t) = - \sum_{i = 1}^{N} \frac{1}{N} log_2 \frac{1}{N} = log_2 N
といった結果になるかと思います.
つまりこの結果から__不純度が最も低ければエントロピーの値は0,不純度が高くなればなるほどエントロピーの値が大きくなる__ことがわかります.
エントロピーを使って,ノードの不純度を数値化できそうですね.
各ノードの不純度が数値化できるようになりましたが,どうやってノードのデータを上手く分割できたかを判断するのでしょうか?
それは今求めたエントロピーを使って利得(Gain)を計算することで簡単に求まります.
以下に式を示します.
\Delta I_H(t) = I_H(t_B) - \sum_{i=1}^{b} w_i I_{Hi} (t_{Ai})
bは分岐(ブランチ)の数,tBは分岐前のノード,tAは分岐後のノード,wiは重み(分岐前に対するデータの量の割合)を示しています.
この式は端的に言えば分岐前のエントロピーと分岐後のエントロピーの合計との差を計算しているだけです.
分岐したときに不純度が上手く低くなっていれば,右辺の式の後ろの項の値が小さくなり,結果的に計算結果の値が大きくなるかと思います.
つまり,この式の計算結果が最大になるような素性と閾値の組というのが,不純度を最大限減らす組であるということです.
これで,エントロピーを使って不純度を最大限減らす組を見つけ出すことができます.
また,この分割指標を用いて決定木を構築していくアルゴリズムが__C4.5__です.
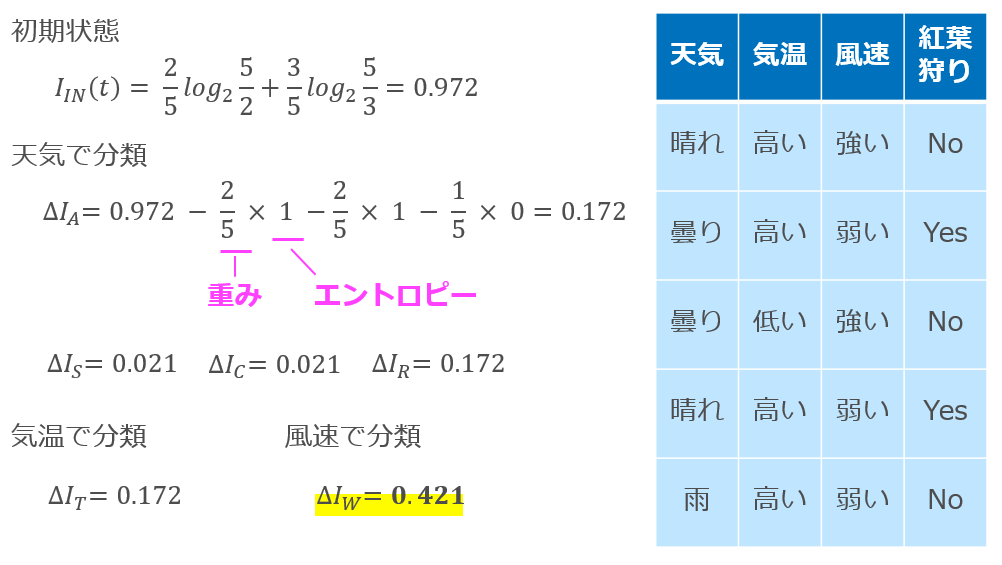
式や文章が多くわかりにくかったかもしれないので,以下に「紅葉狩りに行くか否かを天気・気温・風速という素性から決定するモデルの構築」の初期状態での計算例を示します.
(この例についてはこちらを参考にしました.)
全てのデータの揃った状態でのエントロピーは0.972です.
ここから,「天気が晴・曇・雨」「天気が晴か否か」「天気が曇か否か」「天気が雨か否か」「気温が高いか低いか」「風速が強いか弱いか」という観点でそれぞれ分類を行い,利得を計算しています.
この例では「風速が強いか弱いか」で分類をすると一番利得が大きくなったので,ルートノードは「風速が強いか弱いか」を基準として分類するという結果になります.
以上がエントロピーの意味とC4.5についてです.
次はもう一つの指標であるジニ不純度とCARTの話です.
ジニ不純度の意味とCART
ジニ不純度とはもともと計量経済学の分野で社会における所得分配の均衡・不均衡を表すものとして使われているものらしいです.
このジニ不純度は以下の式で定義されます.
I_G(t) = 1- \sum_{i = 1}^{c} p(i|t)^2 \\
ただし,p(i|t) = \frac{n_i}{N} \\
cは目的変数のクラス数,tは現在のノード,Nはトレーニングデータのサンプル数,niはクラスiに属するトレーニングデータの数を示しています.
この式についても同様に,クラス数が3,サンプル数が9,赤のサンプル数が3,青のサンプル数が2,緑のサンプル数が4といった対応で考えてみてください.
さきほどと同様に任意のノードについてジニ不純度を簡単に求められることがわかりました.
では,このジニ不純度とノードの不純度にどのような関係があるのかを見ていきたいと思います.
ノードの不純度が最も低い場合のジニ不純度を計算してみると
I_G(t) = 1- \sum_{i = 1}^{1} (\frac{N}{N})^2 = 0
といった結果になるかと思います.
同様にノードの不純度が最も高い場合のジニ不純度を計算してみると
I_G(t) = 1- \sum_{i = 1}^{N} (\frac{1}{N})^2 = 1 - \frac{1}{N}
といった結果になるかと思います.
つまりこの結果から__不純度が最も低ければジニ不純度の値は0,不純度が高くなればなるほどジニ不純度の値が1に漸近する__ことがわかります.
エントロピーと同様,ジニ不純度を使ってもノードの不純度を数値化できそうですね.
各ノードの不純度が数値化できるようになりましたが,どうやってノードのデータを上手く分割できたかを判断するのでしょうか?
それはエントロピーと同様に利得(Gain)を計算することで簡単に求まります.
以下に式を示します.
\Delta I_G(t) = I_G(t_B) - w_L I_G(t_L) - w_R I_G(t_R)
tBは分岐前のノード,tLおよびtRはそれぞれ分岐後の左ノード右ノード,wLおよびwRはそれぞれ分岐後のノードの重み(分岐前に対するデータの量の割合)を示しています.
この式は端的に言えば分岐前のジニ不純度と分岐後の左右のノードのジニ不純度の合計との差を計算しているだけです.
エントロピーのときと同様,分岐したときに不純度が上手く低くなっていれば,右辺の式の後ろ2つの項の値が小さくなり,結果的に計算結果の値が大きくなる形になっています.
ジニ不純度の場合もこの式の計算結果が最大になるような素性と閾値の組というのが,不純度を最大限減らす組であるということです.
これで,ジニ不純度を使って不純度を最大限減らす組を見つけ出すことができます.
また,この分割指標を用いて決定木を構築していくアルゴリズムが__CART__です.
エントロピーのときと同様,式や文章が多くわかりにくかったかもしれないので,エントロピーのときと同じ計算例をジニ不純度でやってみます.

全てのデータの揃った状態でのジニ不純度はは0.48です.
ここから,「天気が晴か否か」「天気が曇か否か」「天気が雨か否か」「気温が高いか低いか」「風速が強いか弱いか」という観点でそれぞれ分類を行い,利得を計算しています.
この場合も「風速が強いか弱いか」で分類をすると一番利得が大きくなったので,ルートノードは「風速が強いか弱いか」を基準として分類するという結果になります.
以上がジニ不純度の意味とCARTについてです.
その他細かい点
- 説明変数の連続値の扱い方について
これは任意の素性値についてソートを行い,各要素間の中間値を算出します.
求められた各々の中間値を閾値として分類を行い利得を算出するそうです.
- C4.5とCARTの扱える問題
C4.5は分類,CARTは分類と回帰に対応しています.
- C4.5とCARTによって生成される木
C4.5ではN分木,CARTでは2分木が生成されます.
これは利得の式から自明かと思います.
過学習と予防策
ここの話はこちらがとても参考になりました.
このサイトを読んで,色々調べると理解が深まるかと思います.
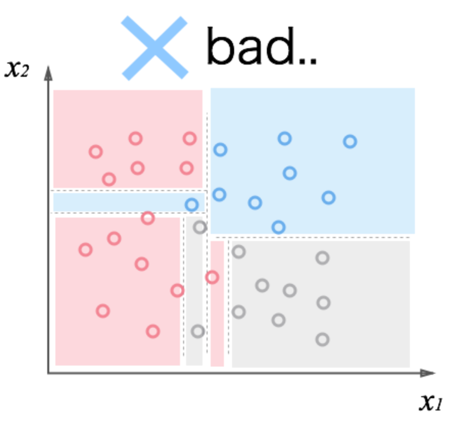
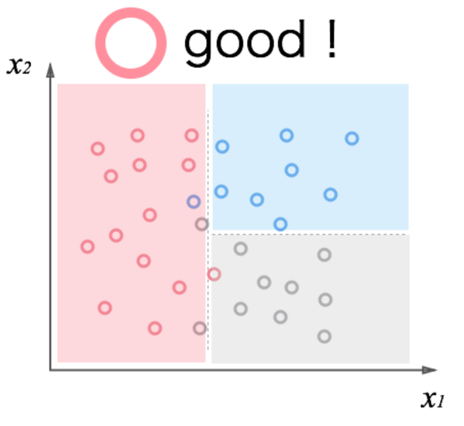
今回は図を引用させて頂きます.
上の図と下の図,どちらのモデルの方がいいと思いますか?
たしかに,精度的には上の図の方が正確に分類できていそうですが,それ以外の値が来ると誤った判定をしてしまう可能性も見えてきて,いわゆる過学習の状態になっています.
下の方がデータの特性をキチンと表せています.
では実際に決定木を構築する際にこのような過学習に陥らないためにはどうすればいいのか.
方針としては「複雑にならないように木の深さを制限する」「木を生成した後に枝を剪定する」といったアプローチがあります.
前者については探索の深さを制御するだけなので簡単そうですね.
後者については例えば以下のような評価関数によって実現できるようです.

分割指数というのは上の説明の利得のことです.
分割指数が小さいということは分割がうまくいっていない,またノードに割り当てられるデータ数が少ないとそれはあるポイントのデータに特化しすぎているという考え方です.
ですので,閾値以上であれば枝を残し,それ以外については探索しないといった制御を行うことで実現できそうですね.
実装(Python + scikit-learn)
理論の話ばかりだと現実味がないので最後にscikit-learnで決定木の学習と推論について簡単に実装して,それに有名なアヤメのデータセットをclosedな状態で使ってみようと思います.
ソースコード
from sklearn.datasets import load_iris
from sklearn import tree
def main():
# アヤメのデータを読み込む
iris = load_iris()
# アヤメの素性(説明変数)はリスト
# 順にがく片の幅,がく片の長さ,花弁の幅,花弁の長さ
# print(iris.data)
# アヤメの種類(目的変数)は3種類(3値分類)
# print(iris.target)
'''
今回の内容と関係ありそうなパラメータ
criterion = 'gini' or 'entropy' (default: 'gini') # 分割する際にどちらを使うか
max_depth = INT_VAL or None (default: None) # 作成する決定木の最大深さ
min_samples_split = INT_VAL (default: 2) # サンプルを分割する際の枝の数の最小値
min_samples_leaf = INT_VAL (default: 1) # 1つのサンプルが属する葉の数の最小値
min_weight_fraction_leaf = FLOAT_VAL (default: 0.0) # 1つの葉に属する必要のあるサンプルの割合の最小値
max_leaf_nodes = INT_VAL or None (default: None) # 作成する葉の最大値(設定するとmax_depthが無視される)
class_weight = DICT, LIST_OF_DICTS, 'balanced', or None (default: None) # 各説明変数に対する重み
presort = BOOL (default: False) # 高速化のための入力データソートを行うか
'''
# モデルを作成
clf = tree.DecisionTreeClassifier(max_depth = 3)
clf = clf.fit(iris.data, iris.target)
# 作成したモデルを用いて予測を実行
predicted = clf.predict(iris.data)
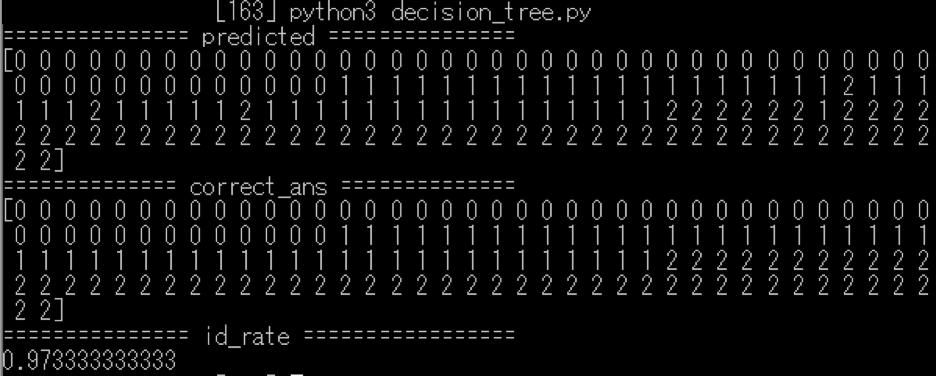
# 予測結果の出力(正解データとの比較)
print('=============== predicted ===============')
print(predicted)
print('============== correct_ans ==============')
print(iris.target)
print('=============== id_rate =================')
print(sum(predicted == iris.target) / len(iris.target))
'''
feature_namesには各説明変数の名前を入力
class_namesには目的変数の名前を入力
filled = Trueで枝に色が塗られる
rounded = Trueでノードの角が丸くなる
'''
# 学習したモデルの可視化
# これによって同じディレクトリにiris_model.dotが出力されるので中身をwww.webgraphviz.comに貼り付けたら可視化できる
f = tree.export_graphviz(clf, out_file = 'iris_model.dot', feature_names = iris.feature_names,
class_names = iris.target_names, filled = True, rounded = True)
if __name__ == '__main__':
main()
(_pydotplus_なるものを使うとdotをpdfに変えてくれるとか...試してません,ごめんなさい.)
実行結果
実行結果は以下のようになるかと思います.
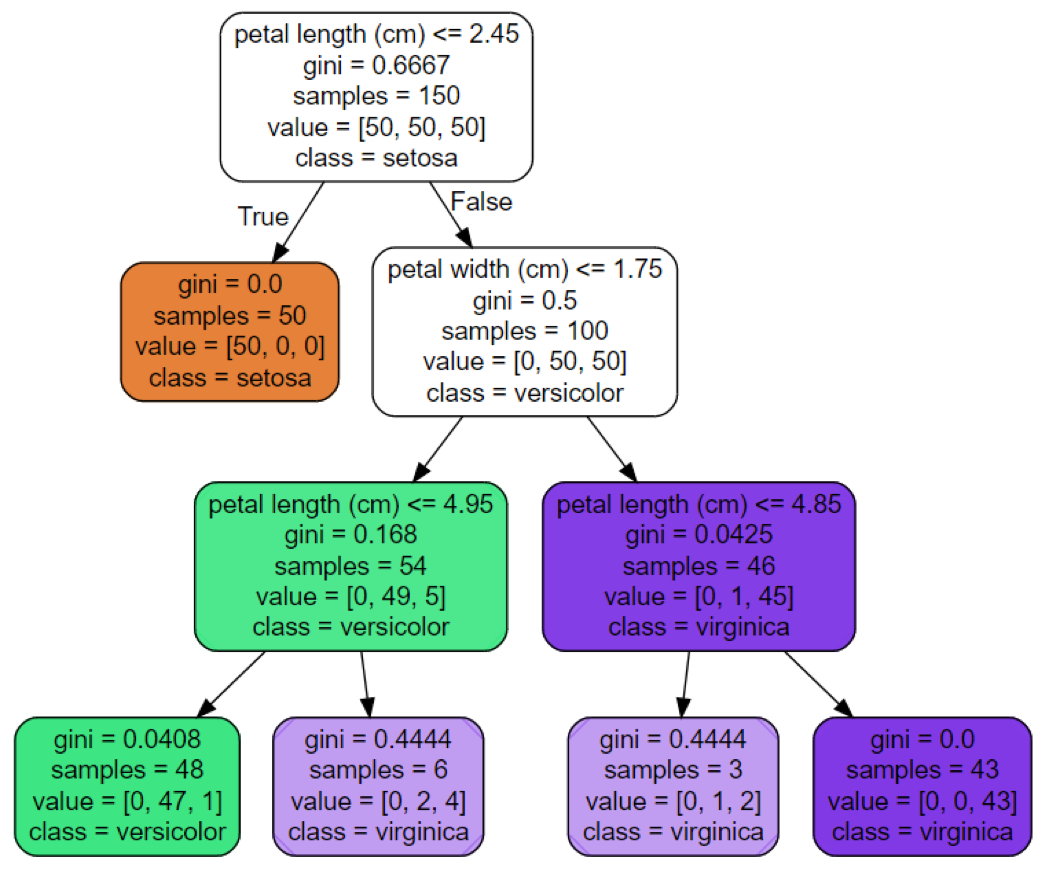
またdotファイルをgraphvizにかけると以下のような結果が得られると思います.
これで実際にアヤメの品種はどのような基準で分類するといいのか一発でわかりますね.
面白い!!!
まとめ
最後までじっくり読んでくれた方,読みにくい記事を最後までよんで頂きありがとうございます.
「なるほどね!」「かゆい所に手が届いた!」みたいな方が少しでもいてくれたら幸いです.
本当はこの木の最小化はNP完全だとか理論の真面目な話もやりたかったのですが,僕の学習が間に合いませんでした.
頭悪い...笑
またいつか勉強したときに別記事にします.
明日はP&Dの代表が記事を書いてくれるので期待大です!
みなさん楽しみにしましょう!
参考文献
以下の文献のおかげで本当に勉強になりました.
参考になる記事をまとめてくださりありがとうございます.
決定木アルゴリズム
決定木とは|マーケターのための データマイニング・ヒッチハイクガイド14
決定木、分類木、回帰木の意味と具体例
名義尺度、順序尺度、間隔尺度、比率尺度
決定木による学習
scikit-learn で決定木分析 (CART 法)
決定木学習
決定木の学習
パラメトリックとノンパラメトリック
決定木分析(ディシジョン・ツリー)