ZOZOテクノロジーズ新卒のむーさん(@murs313)です!
ジニ不純度、知らない子なので戯れる。
決定木で同じように使われているエントロピー(情報量)と比べていきます。
名前
ジニ不純度、ジニ分散指標、ジニ多様性指標等と呼ばれている。英語ではGini’s Diversity Index。
コッラド・ジニ(Corrado Gini)が同じく考案したジニ係数とは違うもの。(ジニ係数のアイデアが基になっているそう。)
使われているところ
決定木のアルゴリズムは複数あり、CARTというアルゴリズムでジニ不純度を指標にして決定木を構築することが多いようです。
他のアルゴリズムであるID3,C4.5,C5.0は、エントロピーを指標にして決定木を構築しています。
こちらのアルゴリズムが使われているところをあまり見ないのですが、アルゴリズムが簡単なので決定木を習う際によく取り上げられるのではないでしょうか。(ちなみにCARTと違って多分岐ができますが、回帰木はつくれません。)
Pythonのsklearn.tree.DecisionTreeClassifierや、RのrpartではCARTが使われており、デフォルトの指標がジニ不純度になっています。
定義
定義を見ていきましょう。
決定木のあるノード$t$に対し、ノード内のサンプルが$n$個、ノード内のクラスが$c$個のときを考える。
このノード$t$内で、クラス$i$に属するサンプルの個数を$n_i$とすると、クラス$i$に属するサンプルの割合$p(i|t)$を、
$$ p(i|t) = \frac{n_i}{n} \tag{1} $$
と書く。このとき、ジニ不純度$I_G(t)$の定義は以下。
$$ I_G(t) = 1 - \sum_{i=1}^c {p(i|t)}^2 \tag{2} $$
同じくエントロピー$I_H(t)$の定義は以下。
$$ I_H(t) = -\sum_{i=1}^c p(i|t) \log p(i|t) \tag{3} $$
エントロピーの対数の底はなんでも良いが、ノード内のクラス数$c$にするとエントロピーの最大値が$1$になるのでよく採用される。(後述)
性質
「不純度」らしいことを確認します。
最も純度が高い(不純度が低い)状態である、「ノード$t$に単一のクラスしか入っていない」とき、$c=1,n_i=n$であるので、ジニ不純度は、
$$ I_G(t) = 1 - \sum_{i=1}^1 {\left(\frac{n}{n}\right)}^2 =0 \tag{4}
$$
エントロピーは、
$$ I_H(t) = - \sum_{i=1}^1 \frac{n}{n} \log \left(\frac{n}{n}\right) =0 \tag{5} $$
となり、両指標とも$0$になる。
次に最も純度の低い(不純度が高い)状態である、「ノード$t$内のすべてサンプルが異なるクラスである」とき、$n=c,n_i=1$であるので、ジニ不純度は、
$$ I_G(t) = 1 - \sum_{i=1}^c {\left(\frac{1}{c}\right)}^2 = 1 - \frac{1}{c} \tag{6} $$
となり、エントロピーは、
$$ I_H(t) = - \sum_{i=1}^c \frac{1}{c} \log \left(\frac{1}{c}\right) = \log c \tag{7} $$
となり、各々の上限はクラス数$c$に依る。
(エントロピーの対数の底を$c$にすると$max(I_H(t))=1$となる。)
※「ノード$t$内のすべてサンプルが異なるクラスである」場合で計算したが、「異なるクラスのサンプルが同数入っている」ノードに対しても同じ結果が得られる。($n=3c,n_i=3$など)
プロットして比べてみる
両指標を視覚化するために、2クラス分類($c\leq2$)という条件を設定します。
10%,30%,80%など、表が出る確率が緻密に計算された多種多様のインチキコインが用意されていると思って、そのコインたちのコイントス結果の不純度を見ていきましょう。この場合、クラスは[表,裏]です。
2クラス分類でジニ不純度の最大値は$\frac{1}{2}$なので、合わせるためにエントロピーの対数の底を$4$とします。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
# 表の出る確率
p1 = np.linspace(0.001, 0.999, 100)
# 裏の出る確率
p2 = 1 - p1
# エントロピー
I_H = lambda p1, p2: - p1 * np.log2(p1) /2 - p2 * np.log2(p2)/2
result_ih = np.array([I_H(p1, p2) for p1, p2 in zip(list(p1), list(p2))])
result_ih[np.isnan(result_ih)] = 0
# ジニ不純度
I_G = lambda p1, p2: 1 - p1*p1 - p2*p2
result_ig = np.array([I_G(p1, p2) for p1, p2 in zip(list(p1), list(p2))])
result_ig[np.isnan(result_ig)] = 0
# プロット
plt.plot(p1, result_ih, label = 'I_H')
plt.plot(p1, result_ig, label = 'I_G')
plt.legend(loc = 'upper right')
plt.xticks(np.arange(0, 1.1, 0.1))
plt.yticks(np.arange(0, 0.51, 0.1))
plt.grid(True)
plt.xlabel("The proportion of heads")
plt.ylabel("Impurity")
plt.show()
出力結果
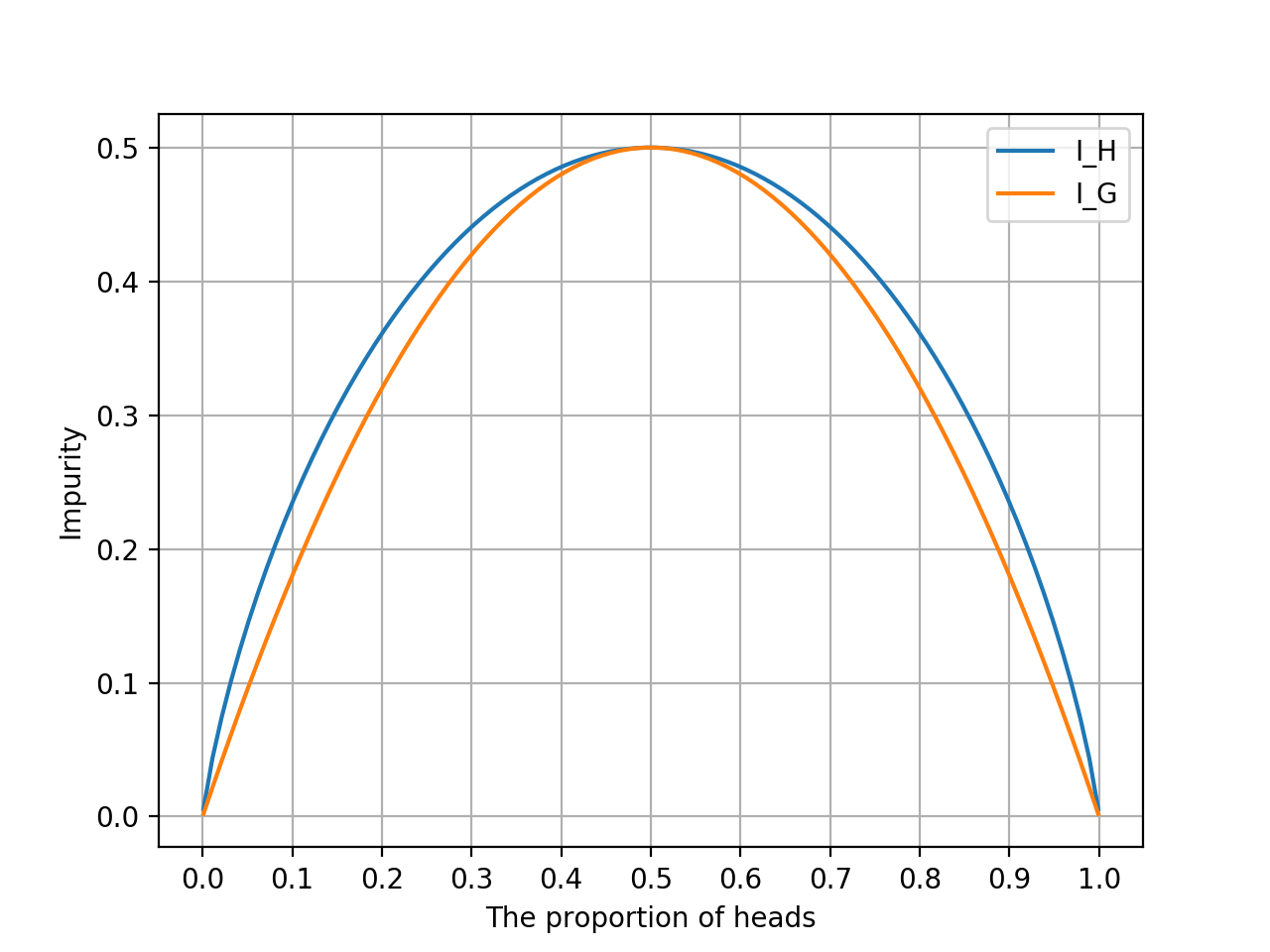
横軸が「表の割合」で、縦軸が各指標です。
表か裏で100%のときは不純度0、半々のときに不純度最大となるという基本性質は同じながらも、湾曲具合が異なりますね。
オレンジ色のジニ不純度の凸の方が鋭いので、中心の変化に敏感そう。
数式で比べてみる
エントロピーの定義式をいじって、ジニ不純度と比べやすくしてみます。
エントロピーの底を$n$とします。
\begin{align}
I_H(t) &= -\sum_{i=1}^c p(i|t) \log_n p(i|t) \\
&= -\sum_{i=1}^c p(i|t) \log_n \frac{n_i}{n} \tag{1より} \\
&= -\sum_{i=1}^c p(i|t) \left(\log_n n_i - 1 \right)\\
&= 1 -\sum_{i=1}^c p(i|t) \log_n n_i \\
\end{align}
一方、ジニ不純度を以下のように冗長に書きます。
$$ I_G(t) = 1 - \sum_{i=1}^c {p(i|t)}{p(i|t)} $$
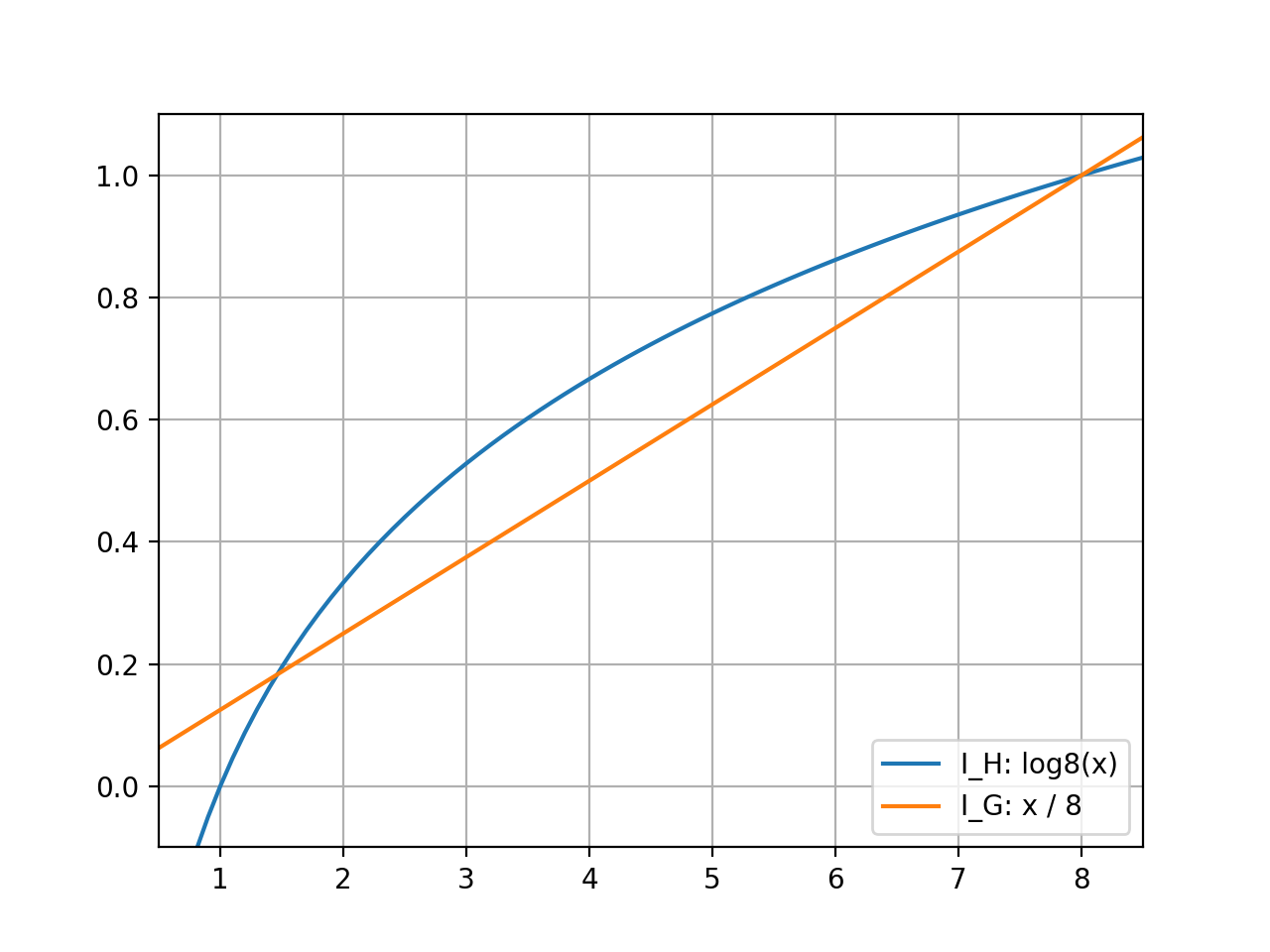
スケールが異なりますが、シグマの中の$\log_n n_i$と$p(i|t)$との違いが湾曲の違いを生み出していたようです。
参考:$n=8$の時の$\log_n n_i$と$p(i|t)$
最後に
ジニ不純度とエントロピーについて見てきました。
エントロピーとさして変わらない指標だな~という印象です。
クラス数が$2$のときに限定されますが、$p=\frac{1}{2}$付近の違いを強く反映させたいときはジニ不純度、$p=\frac{1}{2}$付近はまとめてみたいときはエントロピー、という感じでしょうか。