とりあえず、これまでの投稿内容を「幾何学(Geometry)」なるキーワードで整理してみたのが以下。
【Rで射影幾何学】そもそも「幾何学」とは何か?
さらに近代以降需要概念となった「射影(Projiection)」の概念を導入すると…

c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,type="l",asp=1,main="Absolute Things Rampant Outside the Recognizable Range",xlab="cos(θ)",ylab="sin(θ)")
text(0,0,"?",cex=16)
全ての出発点は「絶地天通」問題。我々人類のちっぽけな知性(Our Poor Little Intelligence)は到底「認識可能範囲外を跋扈する絶対他者(Absolute Things Rampant Outside the Recognizable Range)」を直接は認識し得ないので、とりあえず以下の概念(Concept)を導入(Introduce)してその無限性(Infinity)を認識可能範囲外に明示的に追いやる必要があったのです。
【初心者向け】集合論①部分集合(subset)と真部分集合(proper subset)について。
- その要素数(Element Count)が0から無限(Inf=Infinity)の間で増減する集合(Set)…ここでの投稿においてはしばしば「世界」の訳語を当ててきた。「こちら側」の認識全てを束ねる大前提。
- その要素(Element)全てが、特定の演算に利用可能な(Countable)数列(Number Sequance)…数理(Mathematical Things)の扱う主要対象(Sub Set)で、無限遠の概念すら無限小(-Infあるいは1/Inf)や無限大(Inf)といった形で含む事が可能。
さらにこうした諸概念から派生する形で数直線(Number line)の概念が生じ、さらには(原点0から出発して無限に至る)片側無限数直線(One-side Infinity Number line)や、(符号の概念が付加され、無限小から原点0を経て無限大に至る)両側無限数直線(Two-side Infinity Number line)などの諸概念が現れ、さらにはこれらを直交する(すなわち線型独立性を伴い、互いがその増減の影響を受けずに済む)X軸,Y軸,Z軸…なる数直線の連続で表そうとする直交座標系(Cartesian Coordinate System)によって束ね様とする動きが発生したのです。
線型独立(linearly independent) - Wikipedia -
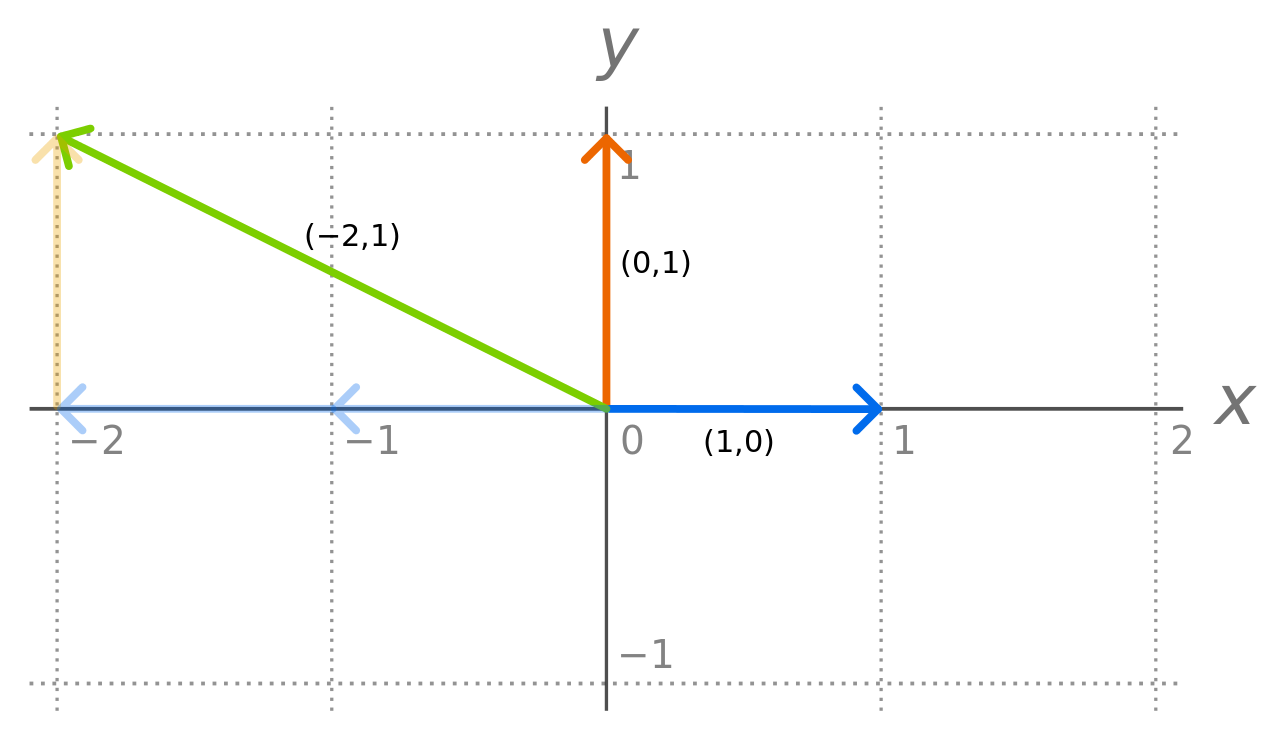
そして、まさにここに(無限小から原点0を経由して無限大に至る)数そのもの(Number itself)の概念を、これらにどう射影(Projection)するかという問題が発生するのでした。
射影(Projection)-Wikipedia-
片側無限数直線(One-side Infinity Number line)
「等差数列あるいは算術数列における0以上の整数」の「数直線上における0から無限大の範囲」に対する射影…それが形成する同心円集合(Concentric Set)における半径(Radius)の間隔は一定。
【Rで球面幾何学】等差数列(算術数列)① 数直線(Number Line)概念の導入(Introduction)について。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ

「等比数列あるいは幾何数列」における1以下の値の「数直線上における0から1の範囲」への射影と、1以上の値の「数直線上における1から無限大の範囲」への射影…それが形成する同心円集合(Concentric Set)における半径(Radius)の間隔自体が動く。
【Rで球面幾何学】等比数列(幾何数列)①その基本的性質について。
【Rで球面幾何学】等比数列(幾何数列)②同心円集合(Concentric Set)に射影(Projection)する準備
(初項a,公差0の等差数列と完全に合致する)初項a,公比1の等差数列を目盛として射影した場合。…まさしく「等差数列そのもの」という感じ。

指数尺(すなわち自然指数関数e^xの値)を目盛として射影した場合。…一般には「対数尺」とか「透視図法」ともいう。この段階でネイピア数の概念が導入される。
【Rで球面幾何学】指数・対数関数の発見

無限大Infと無限小-Infに挟まれた開区間(Open Interval)となる両側無限数直線(Two-side Infinity Number line)
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ
X軸を正負の識別線に採用した両側無限算術数列(Two-Sided Infinite Arithmetic Sequence)

Y軸を正負の識別線に採用した両側無限算術数列(Two-Sided Infinite Arithmetic Sequence)

一方、等比数列は公比(Common Ratio)がマイナスの時、その数列固有の周期と射影される間隔(Interval)が一致する場合に円を描き、それが過剰だと0に向けて収束(Convergence)し。それが過少だと無限に向けて発散(Divergence)する。
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。
公比D=-1の時


0<公比D<-1の時

公比D>-1の時

辺長が無限小(1/Inf)で辺数が無限大(Inf)の円そのもの(Circle Itself)の正多角形による近似(XY座標の確定)。
かくして数学史に円周率πと三角関数の概念が登場してくる。発想自体の起源は古く、古代シュメール時代まで遡る。
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

三角関数の概念の導入には物理学の分野も大いに寄与してきた。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

【初心者向け】「単位円筒」から「単位球面」へ

ガウスが「1の冪根の巡回性」を発見すると多くの人間が円周率πの近似を直接確かめられる様に。またコンピューター・グラフイックの分野にc0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文を提供。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

極座標系(Polar coordinate system)の登場
こうした展開全てを直交座標系のみで束ねるのは難しかったので、各点の座標を原点0からの角度と距離で示す極座標系(Polar coordinate system)が並列して発達。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。

1次元(円周/球表面上の任意の点が対蹠を発見する以前)
「辺長が無限小(1/Inf)で辺数が無限大(Inf)の辺数で構成される円そのもの(Circle / Sphere Surface)上の永劫回帰運動(独:Ewige Regression Bewegung)」の基本概念上、円周/球表面上の任意の点は中心から伸ばされた垂線と垂直に交わる水平線上に位置するとされるが、如何せん直接確かめる手段がないので、まずは「円周角SCAN」によってこれを探し出さねばならない。また実は、探索の結果発見された円周/球表面が、その点が本来属する筈の円そのものである確証を得る方法もなく、この辺りに上掲の「絶地天通」問題がこっそりと埋め込まれているのである。逆をいえば、すなわち以下の操作全てが射影の条件を満たす。
【Rで球面幾何学】単位円と単位球②円周角(Circumference Angle)とは何か?

N次元空間操作
対蹠発見はそのままその円周(Circumference)/球表面(Sphere Surface)上の中心位置(Origin)や半径(Radius)/直径(Diameter)の取得につながり、正弦定理A/sin(a)=B/sin(b)=C/sin(c)=2Rの特殊形たるターレスの定理「その円の弧に対する円周角は常に直角である」の援用も可能となって「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ3次元系の空間処理」なども展開可能となる。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

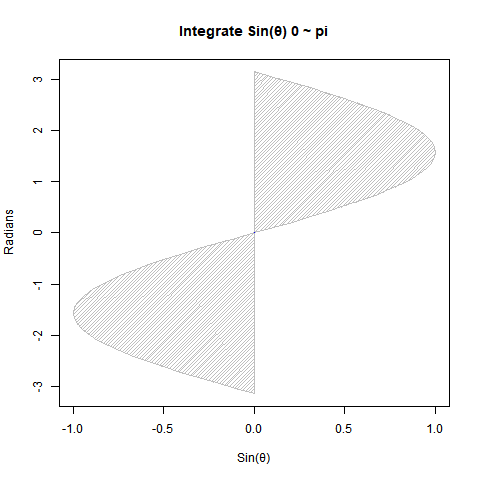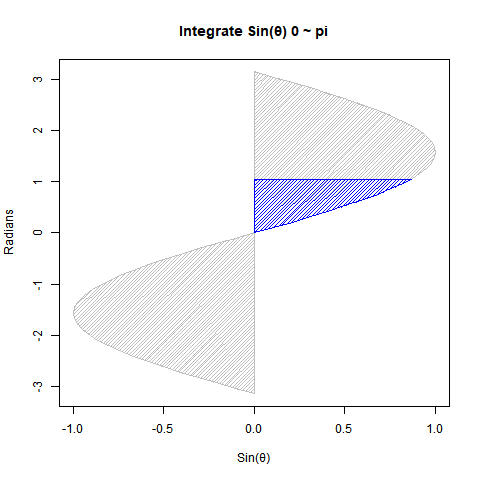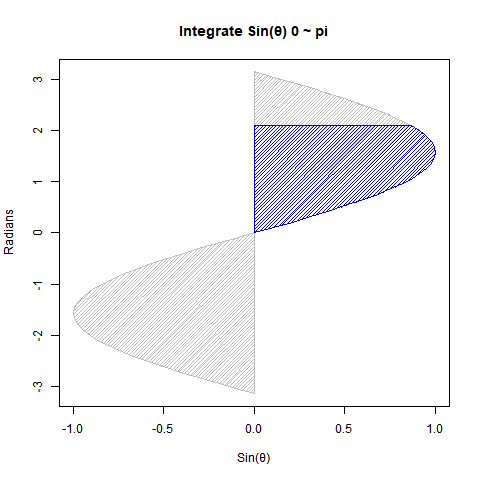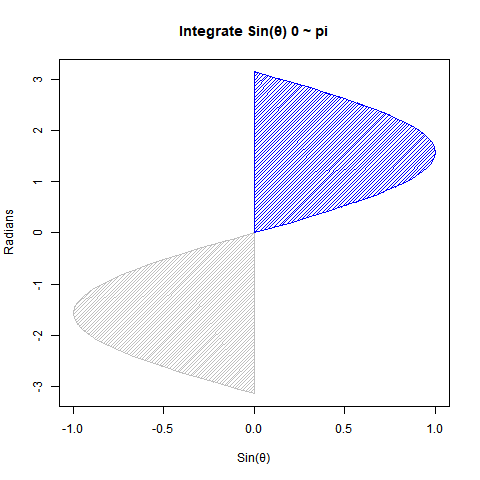
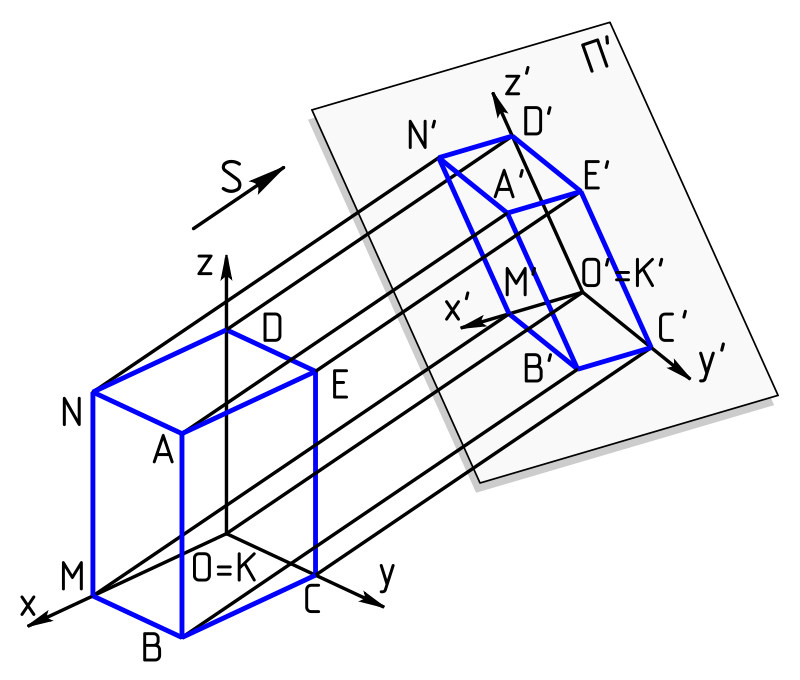
【Rで球面幾何学】単位円と単位球①「半径1」と「直径2」の関係について。
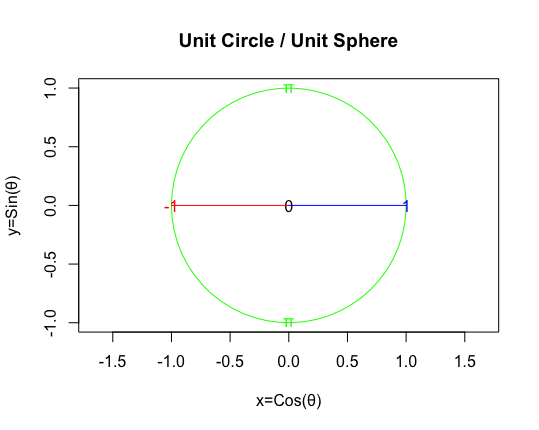
【Rで球面幾何学】ハミルトンの四元数(Quaternion)は何を表しているのか?
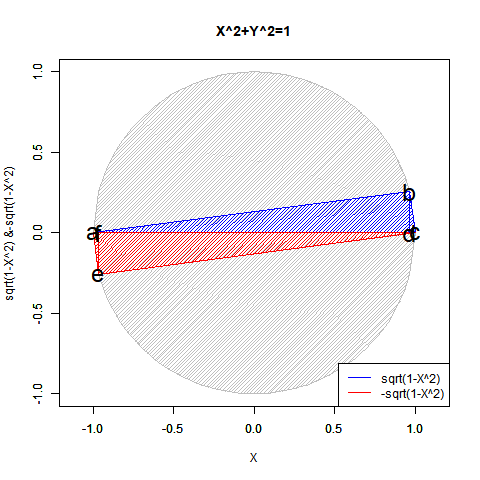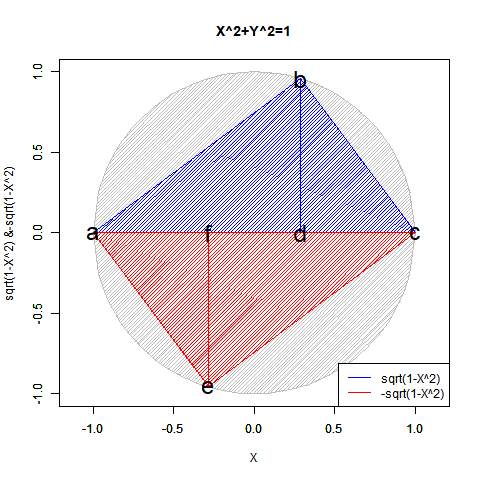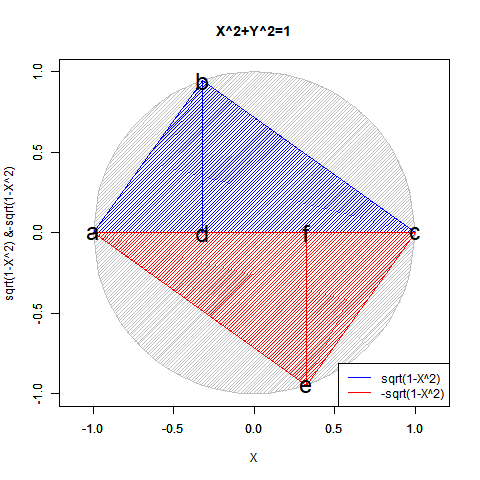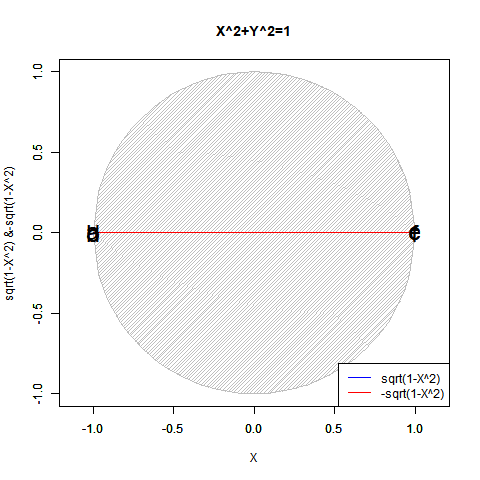
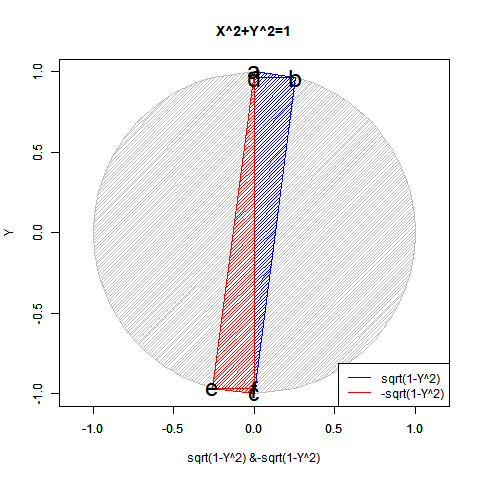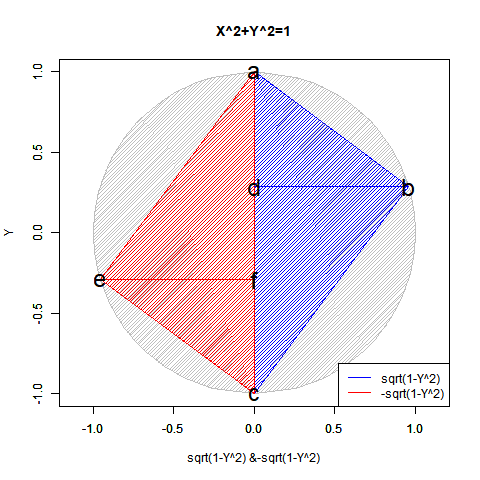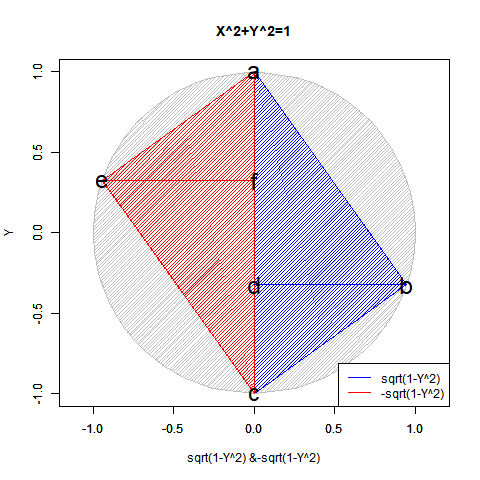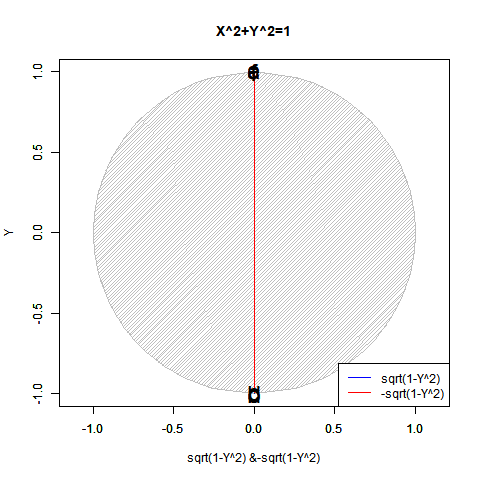
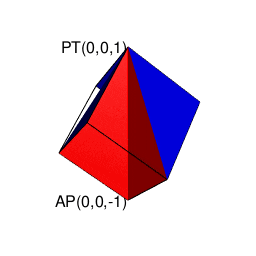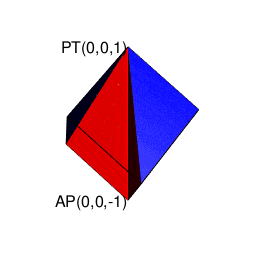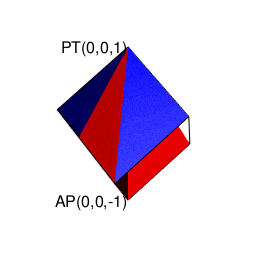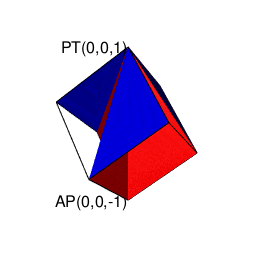
こうして、全体像がかなりスッキリしてきた所で以下続報…