COVID-19 数理モデル〜 SIR と Gompertz と K値の関係〜 #COVID-19

S ≒ 全人口(N)の時の SIR モデル

SIR モデルでは S ≒ N の時、指数関数的に I が増加します。
t = 0 の時の数を I₀ とすると I = I₀e^kt と表せます。
ジョンズ・ホプキンス大学が公表しているデータでは世界のすべての国で未感染者 (S) が全人口 (N) の99%以上あり S ≒ N のため I = I₀e^kt が成り立ちます。
このような指数関数では対数グラフが上向きの直線になります。

指数関数とゴンペルツ効果

指数関数は倍加時間 (doubling time) が常に一定です。現実世界では資源や空間が無限にあるわけではないので指数関数的に増加するものでも一定の倍加時間を保つことはなく、時間の経過とともに増加率が減衰していきます。微量の DNA や RNA を増幅する PCR 法ではサーマルサイクラーの周期を doubling time として指数関数的に template が増加するはずです。しかし実際はサーマルサイクラーの容器の大きさや試薬の量に上限があるため template の増加率は時間とともに減衰します。Schlereth らは PCR 法における template の増加が Gompertz 曲線に従う¹ことを報告しています。Laird は Gompertz 曲線が「all biological growth」に適用できる²と述べています。
対数化したゴンペルツ曲線は以下の式で表せます。

\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}

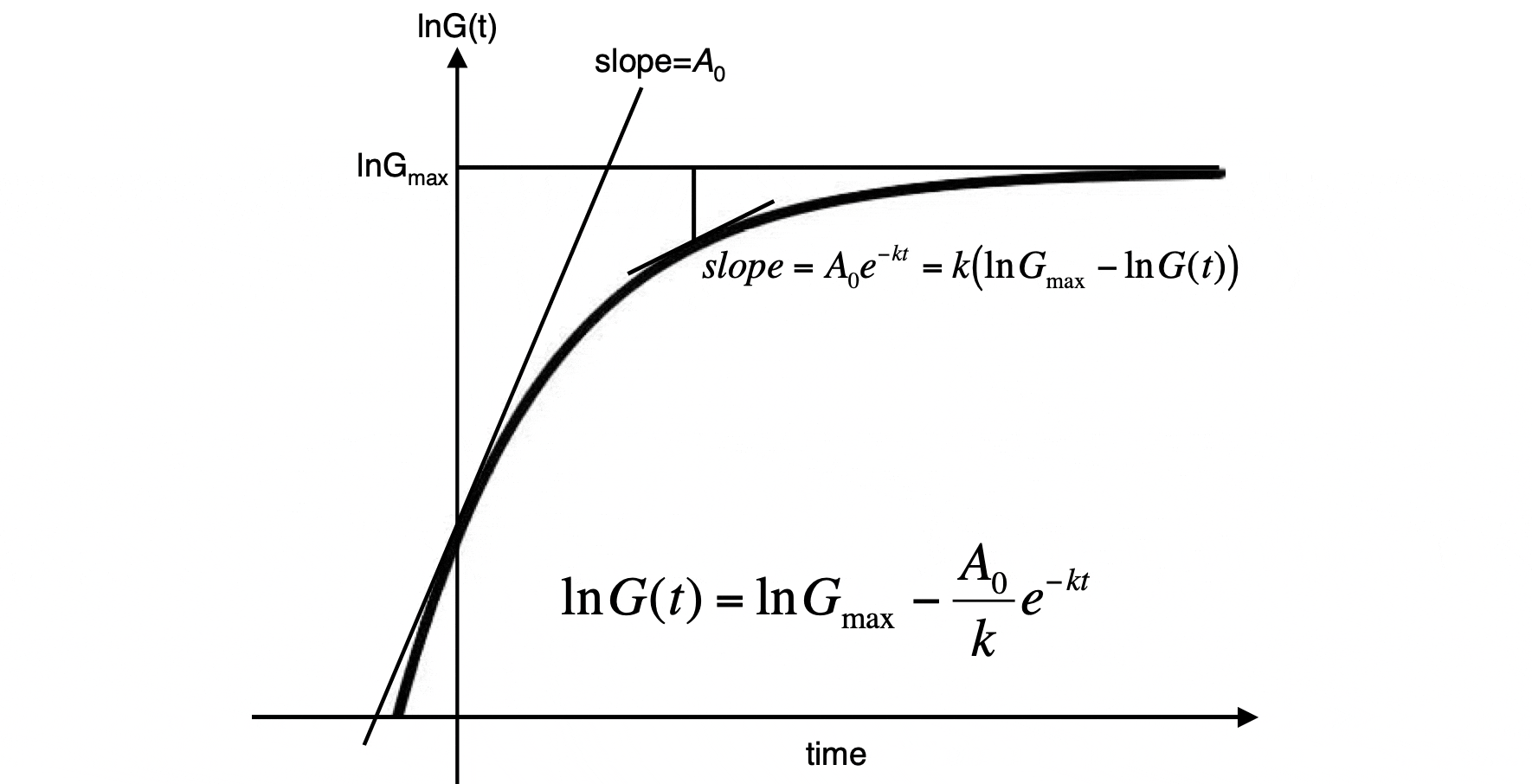
ゴンペルツ曲線では対数化した時の傾き A₀ が時間 (t) の経過とともに e^-kt 倍に減衰し t = ∞ では傾き 0 となります。（ここでの k は前段落の k とは異なります）

対数化しないゴンペルツ曲線は

\ G(t)=ab^{e^{-kt}}

と二重指数関数になります。

世界各国の累積患者数

累積患者数を対数表示 (logarithmic) すると多くの国で傾きが減衰しています。
ゴンペルツ曲線とは何か？（3）で実測値が Gompertz 曲線に当てはまるかを検証する方法を示していますが、かなり良く fit します。
このことから
・S ≒ N の時、指数関数的に I が増加するという SIR モデルの仮定は正しい。
・しかし、現実世界は有限であるためゴンペルツ効果が働く。
ということが推測できます。

中国とブラジルを比べてみる

ロックダウンの代表：中国と、ノーガードの代表：ブラジルを比べてみました。
iPhone アプリ「Gompertz 曲線計算機」で計算すると
中国：

\ G_{max}=81301\\
\ln{G(t)}=11.3058-2.6064e^{-0.1503(t-4)}\\
\ G(t)=81301\times0.0738^{e^{-0.1503(t-4)}}

ブラジル：

\ G_{max}=9256061\\
\ln{G(t)}=16.0408-5.7895e^{-0.0148t}\\
\ G(t)=9256061\times0.0031^{e^{-0.0148t}}

中国では対数グラフの傾きが1日で e^-0.1503 = 0.86倍に減衰。
ブラジルでは1日で e^-0.0148 = 0.985倍に減衰することがわかりました。
この減衰係数 k の違いが
・ロックダウンとノーガードの違い
・人種的背景の違い
・ウイルスの型の違い
・結核や旧型コロナ感染歴の違い
のいずれに由来するかはわかりません。

K値

大阪大学の中野先生が K値という指標を提唱³されました。これは過去1週間の患者発生数を現在の累積患者数で割ったものです。最近 K値と Gompertz 曲線に関する論文⁴も報告されるようになりました。

累積患者数が Gompertz 曲線に従う時の K値

COVID-19 の累積患者数が Gompertz 曲線に従う時 K値はどうなるでしょうか。
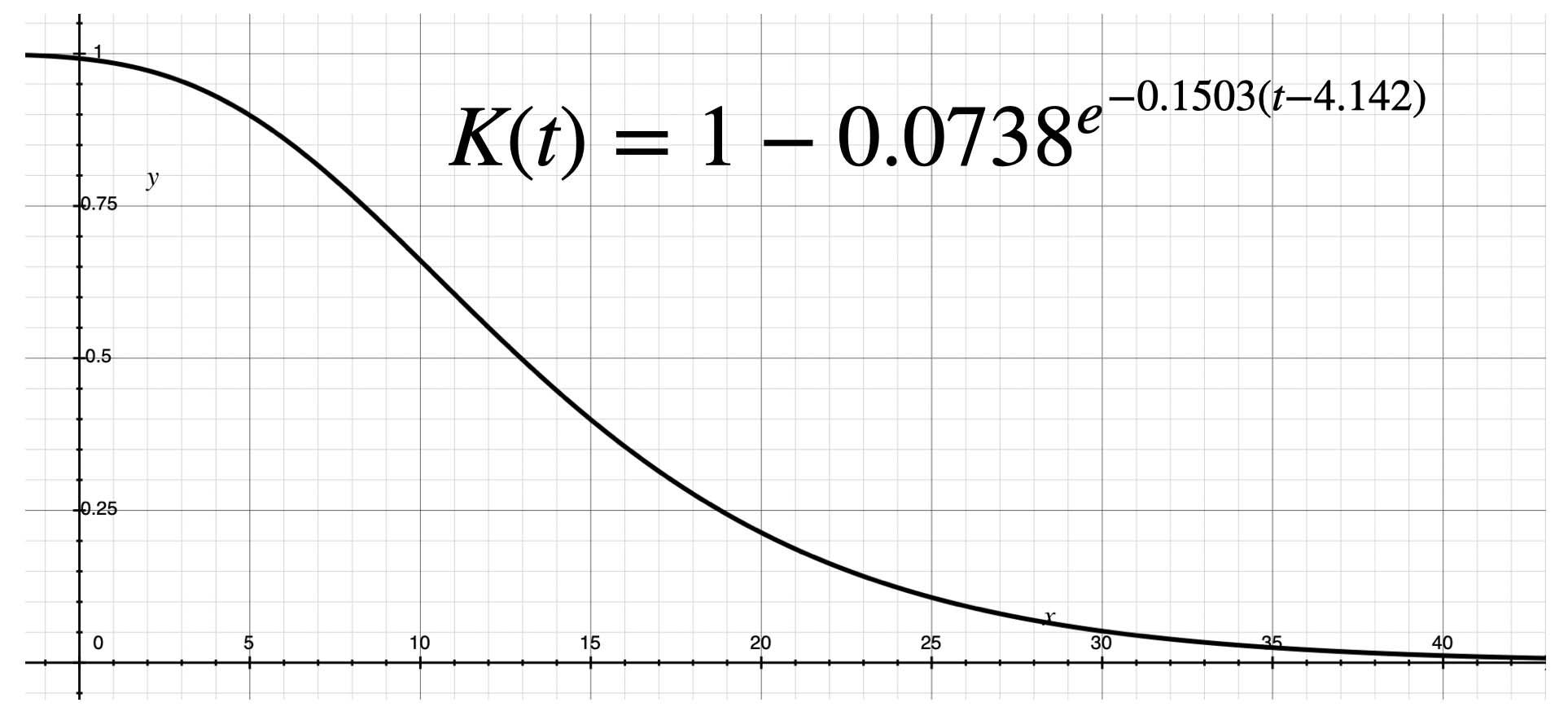
中国の患者数が、

\ G(t)=81301\times0.0738^{e^{-0.1503t}}

に従う時、

\begin{align}
\ K(t)&=1-\frac{81301\times0.0738^{e^{-0.1503(t-7)}}}{81301\times0.0738^{e^{-0.1503t}}}\\
&=1-0.0738^{e^{-0.1503(t-4.142)}}
\end{align}

となり K値は 1-(ゴンペルツ曲線)で下図のような下向き曲線になります。（このカッコ内のゴンペルツ曲線は最大値が1になります）

\ G(t)=ab^{e^{-kt}}

の時

\ K(t)=1-b^{e^{-kt}}

が成り立ちます。
多くの国で K(t) の形状が似通っているのは、累積患者数が Gompertz 曲線に従っているためでしょう。

累積患者数が指数関数の時の K値

累積患者数が I = I₀e^kt のように指数関数になる時 K値はどうなるでしょうか。
I(t) = 10 e^{0.15 t} とします。

\begin{align}
\ K(t)&=1-\frac{10e^{0.15(t-7)}}{10e^{0.15t}}\\
&=0.65
\end{align}

と K(t) は定数になります。

対数表示した時の傾きが e^kt 倍に増大する時の K値

Gompertz 曲線では対数表示した時の傾きが時間 t の経過とともに e^-kt 倍に減衰します。
対数表示した時の傾きが e^kt 倍に増大する時 K値はどうなるでしょうか。

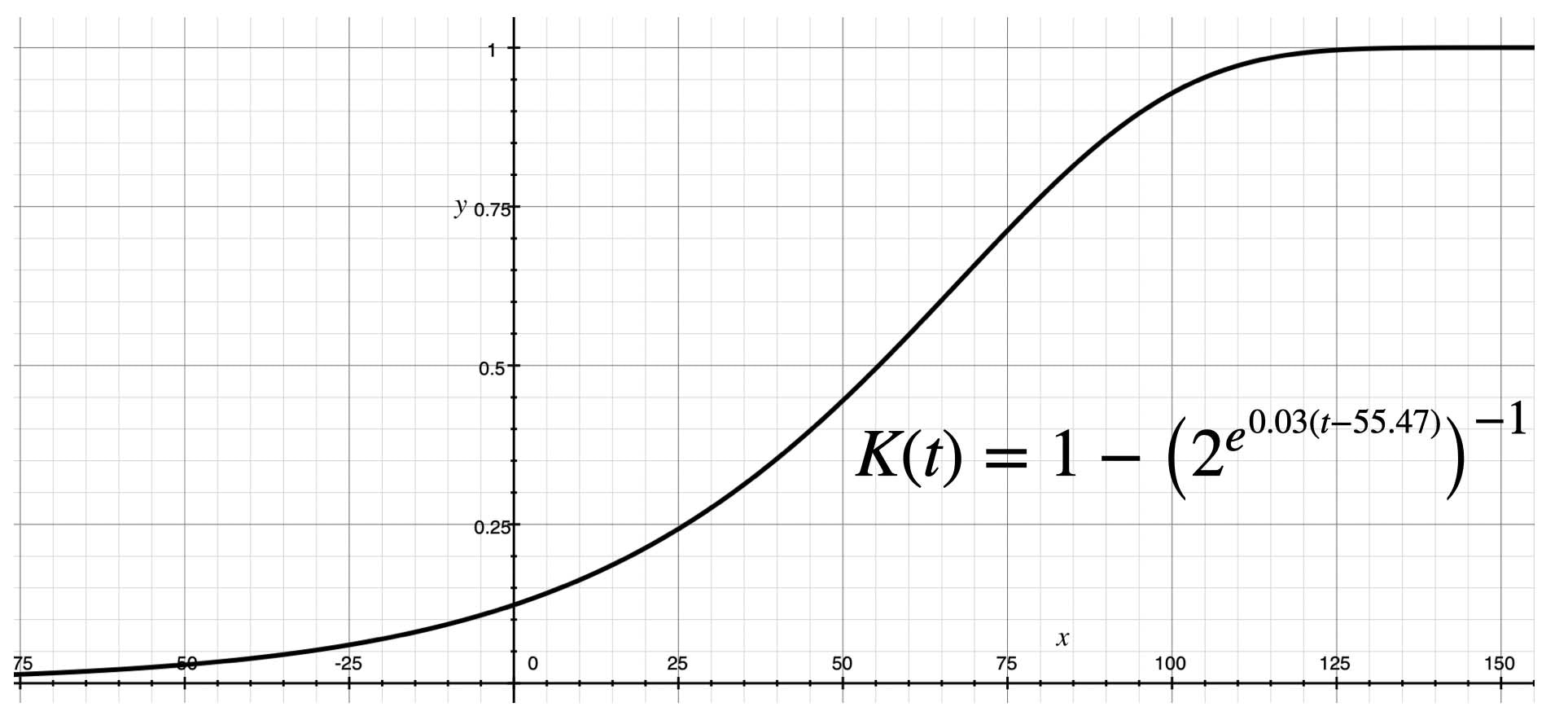
\ G(t)=50\times2^{e^{0.03t}}

とします。

\begin{align}
\ K(t)&=1-\frac{50\times2^{e^{0.03(t-7)}}}{50\times2^{e^{0.03t}}}\\
&=1-\bigl(2^{e^{0.03(t-55.47)}}\bigr)^{-1}
\end{align}

下図のように上向き曲線になります。

K値で増加のトレンドがわかる

以上に示したように累積患者数が
・Gompertz 曲線に従う（倍加時間が延長）時は K(t) = 1 -（ゴンペルツ曲線）の下向き曲線
・指数関数に従う（倍加時間が一定）時は K(t) = 定数
・対数表示した時の傾きが e^kt 倍に増大する（倍加時間が短縮）時は上向き曲線
となることがわかります。
K値によるトレンドの観察は COVID-19 だけでなく他分野にも応用できるかもしれません。
例えば抗癌剤投与時の腫瘍の反応（大きさや腫瘍マーカーの変化など）に使えるかもしれません。

世界各国のトレンド

累積患者数を対数化したグラフをみると国によって様々なパターンがあります。
1) きれいな Gompertz 曲線に従う。
2) 上向きの直線を描く（指数関数的増加）
3) 鏡餅を側面から見た時のような二段階の Gompertz 曲線を描く。
4) 一旦 Gompertz 曲線に乗ったように見えて再び指数関数的に増え始める。
5) 上向きの直線から更に傾きが急峻になる（倍加時間の短縮）
これらの違いは都市封鎖などの介入が影響しているのかもしれません。

日本の場合

日本の累積患者数を対数表示したグラフでは2020年4月中旬までほぼ直線的で指数関数的に増加していました。北海道大学の西浦先生が「このまま増え続ければ40万人死ぬ」とおっしゃったのも頷けます。「3密回避」や「8割削減」などのスローガンのもと国民が行動制限した結果、増加率が減衰していきました。（ゴンペルツ効果の発現）

まとめ

SIR モデルが正しい時 S ≒ N では指数関数的に増加する。
指数関数的に増えようとするものは Gompertz 曲線に従うことが多い。
Gompertz 曲線に従う時 K値は1-（ゴンペルツ曲線）となる。
K値の傾き（上向き・平行・下向き）を観察することでトレンドがわかる。

COVID-19 数理モデル 〜 SIR と Gompertz と K値の関係〜