ゴンペルツ曲線とは何か？（5） #数理モデル

医学・生理学への応用（つづき）

ゴンペルツ曲線とは何か？（4）では C型肝炎ウイルス (HCV) にインターフェロン (IFN) を投与した時の HCV 量が

\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}

と表せることを示しました。
上記曲線の傾きは、

\frac{d\ln{H(t)}}{dt}=-D_0e^{-kt}

となり最初の傾き $\ -D_0$ が時間の経過と共に $\ e^{-kt}$ 倍に減衰することが分かります。
ゴンペルツが観測した人口減少曲線や、生物の増殖曲線では、等しい時間間隔を s とすると
$\ F(ns)$ と $\ F\bigl((n+1)s\bigr)$ の差が $\ mp^n$ となり等比級数的変化を示していました。
$\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}$ も等比級数的変化を示します。

証明
上式を簡単に $\ F(t)=\alpha + \beta e^{-kt}$ とします。

\begin{align}
\ F(ns)-F\bigl((n+1)s\bigr)&=\alpha + \beta e^{-kns}-(\alpha + \beta e^{-k(n+1)s})\\
\ &=\beta e^{-kns}(1-e^{-ks})\\
\ &=\beta (1-e^{-ks})(e^{-ks})^n\\
\end{align}

$\beta (1-e^{-ks})=m, e^{-ks}=p $ と置き換えることができます。（共に定数のため）

\therefore F(ns)-F\bigl((n+1)s\bigr)=mp^n

IFNβによる HCV 減少

2008年の研究ですが C型肝炎の患者に IFNβ を2週間投与して 0週、0.5週、1週、2週の HCV 量を測定しました。Forestier らの論文データ¹を独自に解析した結果、抗ウイルス薬投与初期のウイルス量は極めて正確に

\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}

に一致することが分かっていたので、当院での結果も等比級数的変化を示すことが予測されました。

\ F(0)-F(0.5)=m\\
F(0.5)-F(1)=mp\\
F(1)-F(1.5)=mp^2\\
F(1.5)-F(2)=mp^3\\
\therefore F(2)=F(1)-mp^2-mp^3

しかし計算から予測された値（灰色）と実測値（黒色）には以下のようにズレがありました。

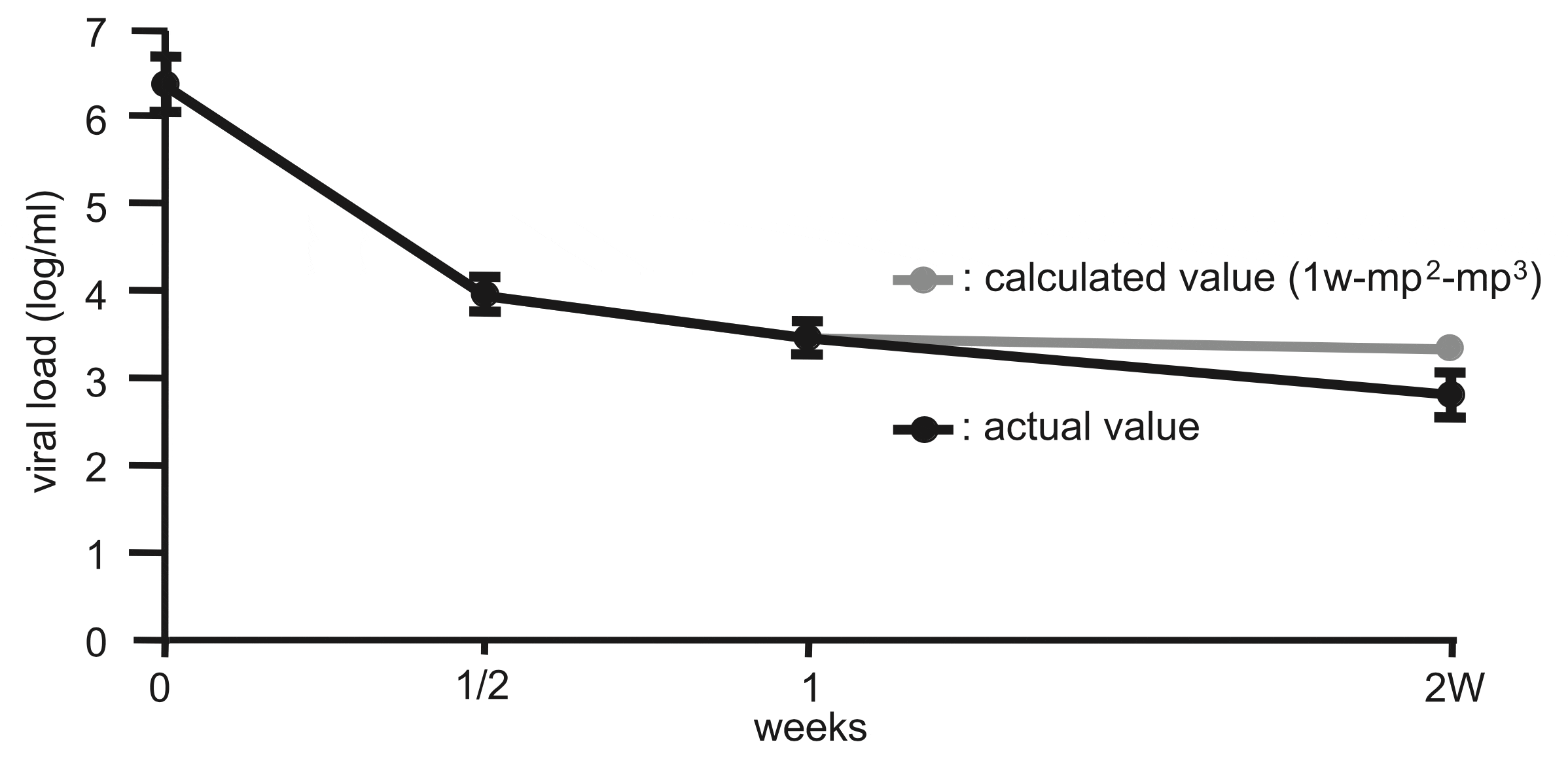
このズレを説明する理論が以下に示す「Gomp-Ex model」です。

Gomp-Ex model

Wheldon は「ある閾値までは指数関数的に増加（exponential growth）し、ある閾値を超えると Gompertz 曲線に従う」という Gomp-Ex model を提唱しました²。

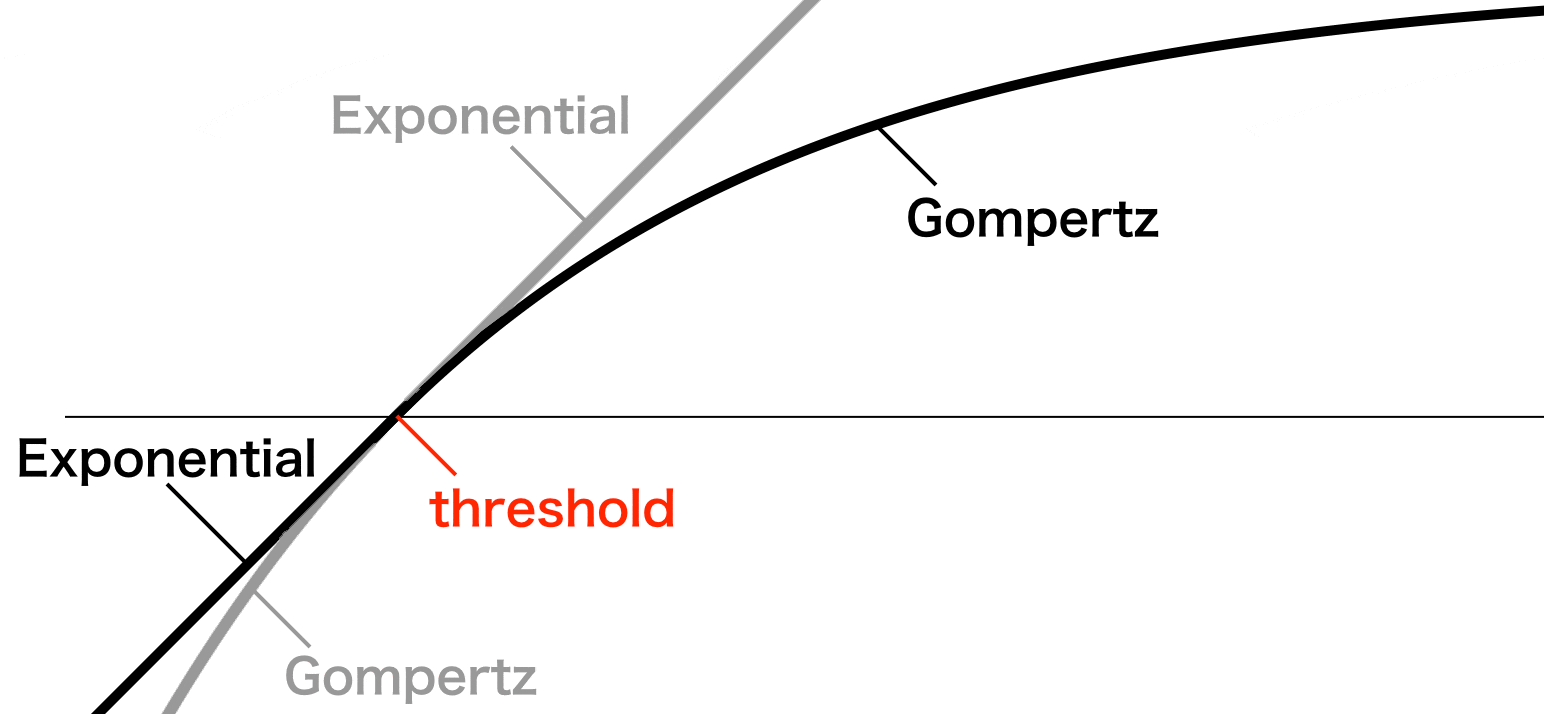
Gompertz 曲線では過去に時間をさかのぼるほど doubling time は短縮して曲線が急峻になります。しかし、いくら時間をさかのぼっても doubling time が細胞固有の細胞周期や PCR のサーマルサイクラーの周期よりも短くなることはないでしょう。

ゴンペルツ曲線とは何か？（4）で

子宮内の胎児の成長も Gompertz 曲線に従います。
1個の受精卵は1日で2個に分裂します。（doubling time 1日)
一方 1500グラムの胎児が3000グラムに倍増するには2ヶ月かかります。(doubling time 2ヶ月)
もし胎児の成長の doubling time が最初から最後まで2ヶ月であったなら、1個の受精卵が1cmになるまでに5年かかってしまいます！（そんなことは有り得ませんね）
実際は 1個の受精卵はわずか1ヶ月で1cm大（10億個)まで増殖します。

と述べました。10億 = 10の9乗 = 2の30乗であることから、受精卵が1個から10億個に増えるまでの30日間は doubling time = 1日を維持していることが分かります。このことからヒト胎児の成長は Gomp-Ex model に従っているのです。

HCV の減少曲線

\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}

では t = ∞ の時

\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}

という有限の最小値に収束します。しかしこれでは永久に HCV は根絶できないことになります。
もし HCV の増殖が Gomp-Ex model に従うなら減少曲線はどうなるでしょうか？

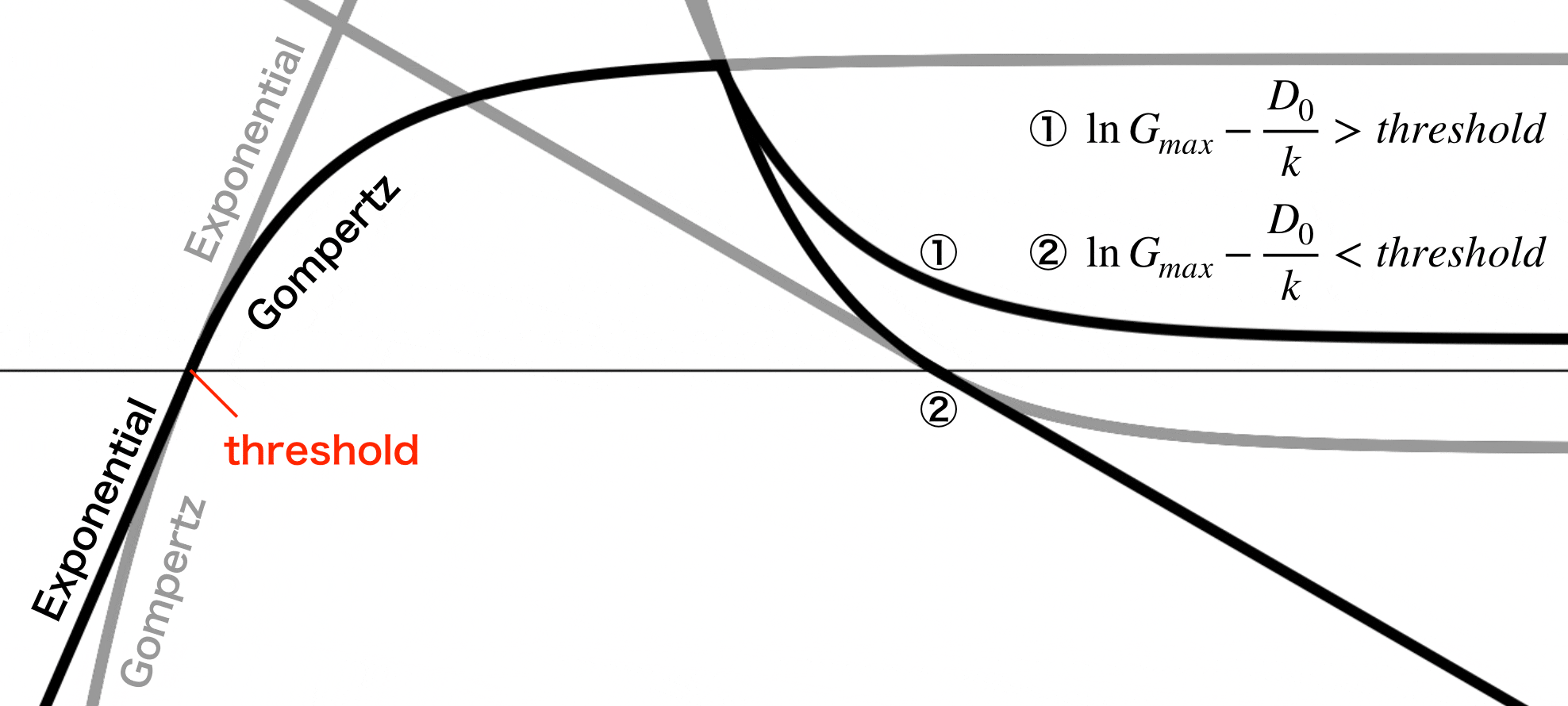
①：$\ln{G_{max}}-\frac{D_0}{k}$ が閾値より大きい場合、減少曲線は $\ln{G_{max}}-\frac{D_0}{k}$ に収束します。

②：$\ln{G_{max}}-\frac{D_0}{k}$ が閾値を下回る場合、減少曲線は閾値に達した時の傾きを維持して直線的に減少します。

当院のデータでは「IFNβ を投与して2週間の HCV ウイルス量が3.5を下回るかどうか」で HCV が根絶できるかどうかが予測できたので Gomp-Ex の閾値は3.5であると推測しました³。

以下は古いデータですが2009年の New England Journal of Medicine に掲載されたペグインターフェロン+リバビリン使用時の HCV 減少⁴を独自に数式化したものです。

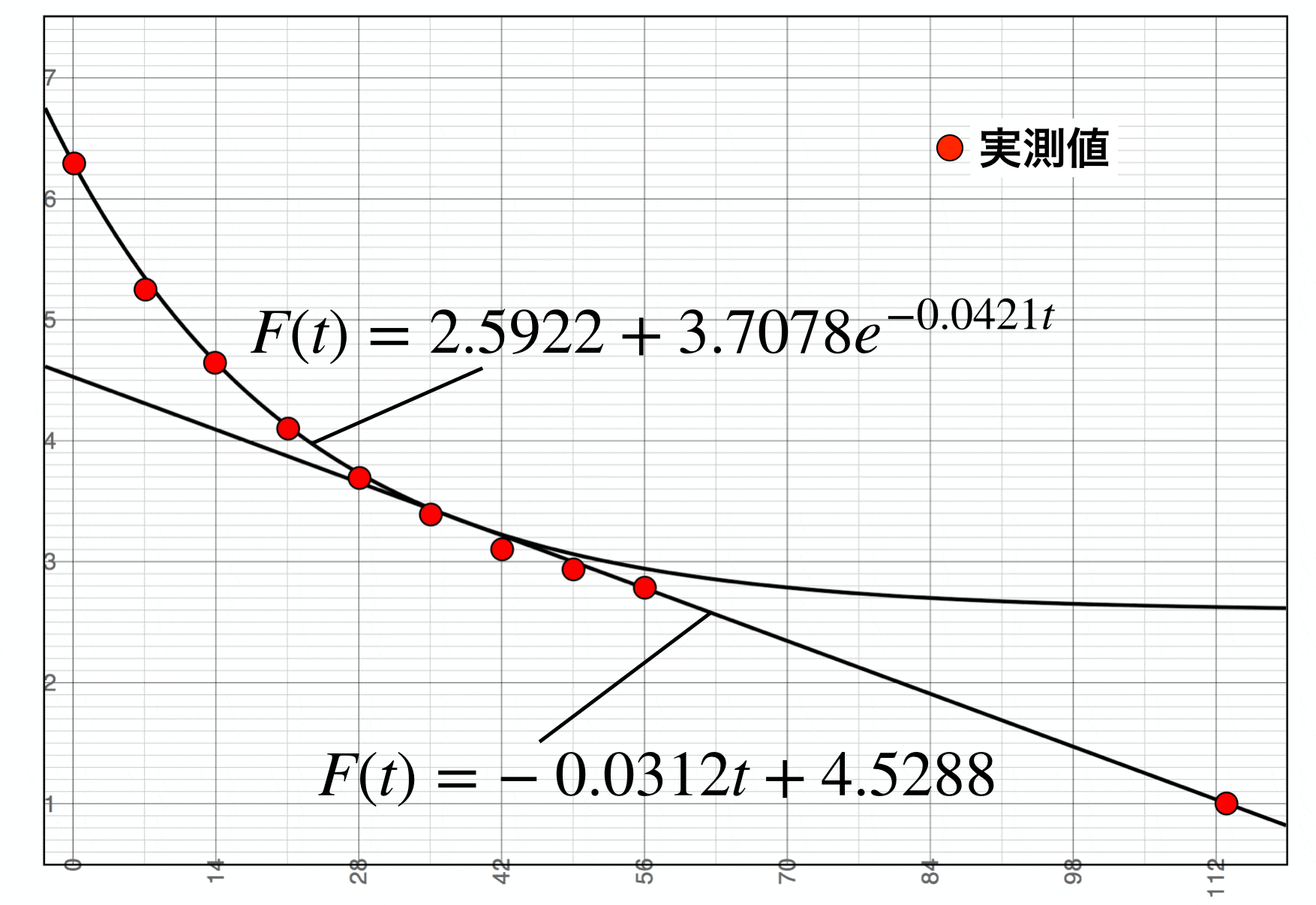
\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}

に当てはまる早期の曲線相と、後期の直線相から構成されていることが分かります。曲線相と直線相の閾値は、およそ3.5（縦軸）であり、当院の IFNβ 投与で推測した閾値と一致しました。

Gompertz-Matsui model のその後

私が2008年に上記モデルを考案した頃は、HCV の治療に IFN が使われており治癒率はおよそ50%でした。そのため治療の有効性を予測するモデルを発表しました。
このモデルは全く普及しないまま数年が経過しました。
現在では IFN を使用しない新薬（Direct Acting Antivirals: DAA）が登場し、HCV の治癒率はほぼ100% となりました。従って有効性の予測モデルも必要なくなりました。
医学の進歩は素晴らしいものです。
ただ、せっかく考えたモデルが忘れ去られてしまうのは残念なので SEO 力の高い Qiita に投稿させていただきました。
今後の応用としては「抗癌化学療法の最適化」に使えるのではないかと考えています。
もし抗癌剤投与時の癌細胞の減少が

\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}

に当てはまり、腫瘍の増殖が Gomp-Ex model に従うならば
$\ln{G_{max}}-\frac{D_0}{k}$ が Gomp-Ex の閾値を下回れば癌が根治する可能性が出てくるのです。また、直線相の式から根治までの最適な投薬期間が推測できるでしょう。

※IFNβ（インターフェロン・ベータ）：DAAの登場以降、HCV の治療に使われることはなくなりました。現在では MERSコロナウイルスに対する有効性が研究されています⁵ ⁶。2020.7.13 の Science に COVID-19 で重症化する患者における内因性 IFN の欠乏と肺組織内ウイルス量の増加が報告され IFN 療法が期待されています⁷。

"type I IFN deficiency is a hallmark of severe COVID-19 and infer that severe COVID-19 patients might be potentially relieved from the IFN deficiency by IFN administration" J. Hadjadj et al., Science 10.1126/science.abc6027 (2020).

おわりに

「累積バグ発生数」の話から大幅に飛躍してしまいましたが、Gompertz 曲線の考え方は情報工学だけでなく医学・生理学にも広く応用できます。工学系の学生さんは医学・生物学系の学生さんにもこのページを紹介していただければ幸甚です。
次章（6）では「新型コロナウイルス (COVID-19) の累積患者数は Gompertz 曲線に従うか？」に関して検証します。