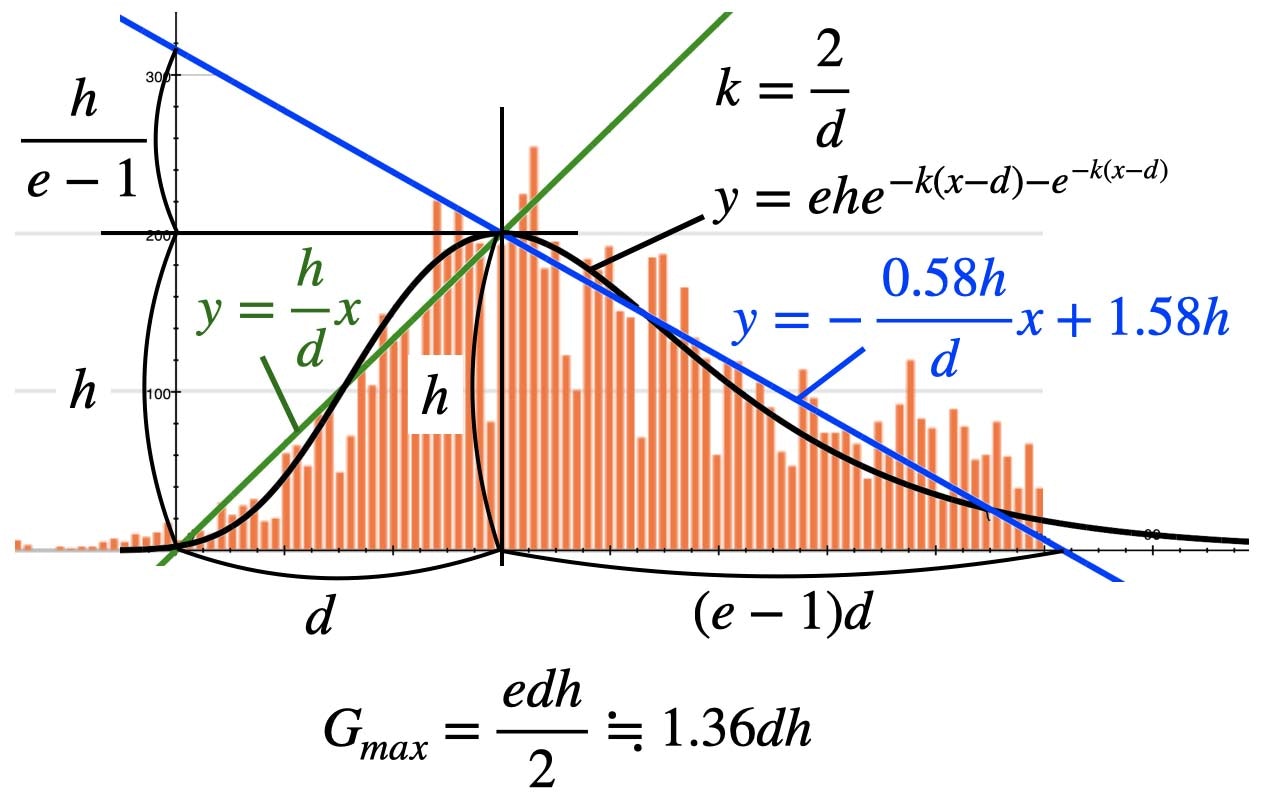
新型コロナ新規発生数を一次関数で近似する。

ゴンペルツ曲線とは何か？（12）で COVID-19 の累計感染者数と新規感染者数が以下のように表せることを示しました。（G_max：それぞれの波毎の総感染者数、k：減衰係数）

\begin{align}
\ G(t)&=G_{max}e^{-e^{-kt}}\\
\frac{dG}{dt} &=kG_{max}e^{-kt-e^{-kt}}\\
\end{align}\\

2020.3.1 (day 0) - 2021.2.19 (day 355) の全経過を単一の式、一本の曲線で、ほぼ完全に近似できました。（計算式と実測値の相関係数: R² = 0.9999）
上式は二重指数関数であり描画するためには Mac の Grapher やエクセルなどのソフトが必要です。本稿では、より簡易に描画できるように新規発生数を一次関数で近似する方法を示します。

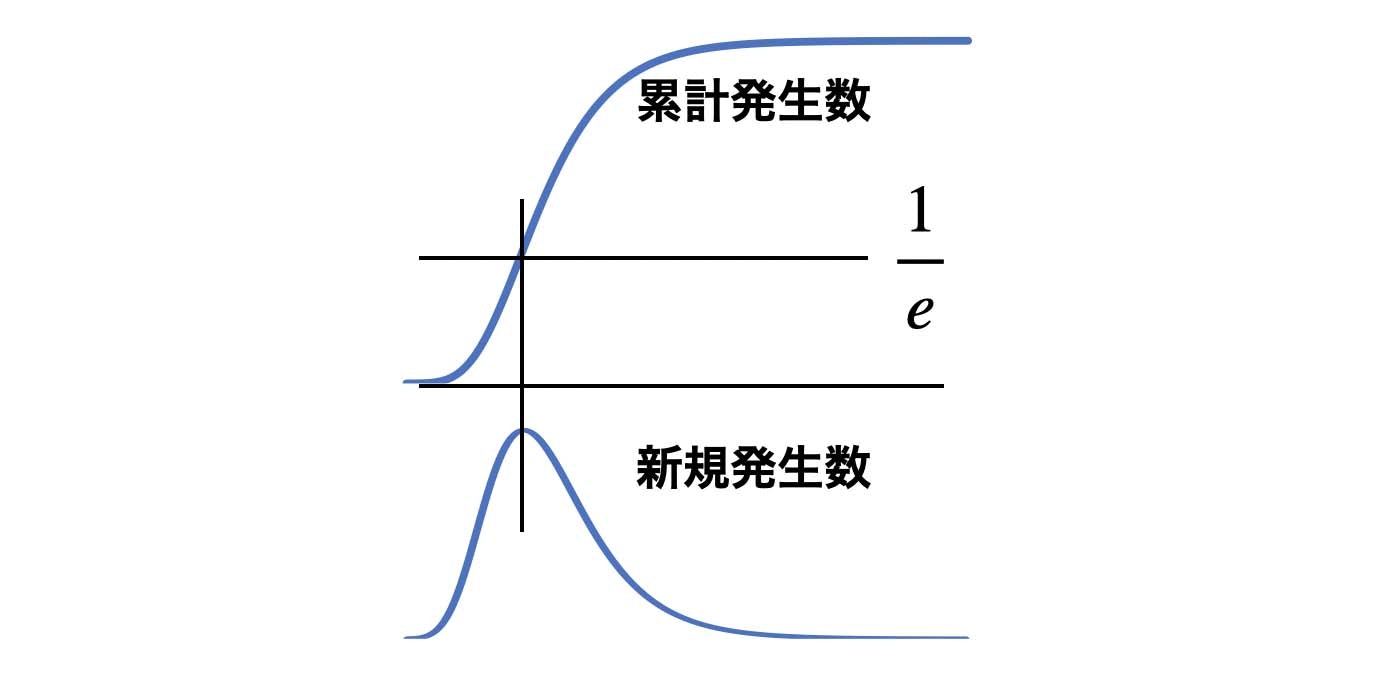
上図のようにゴンペルツ曲線は累計発生数が最大値の 1/e に達した時が変曲点となり新規発生数がピークに達します。
開始からピークまでの上り坂とピークから終息までの下り坂を2本の直線で近似します。
開始からピークまでの日数を d、ピーク時発生数を h とします。
新規発生数を二重指数関数で表すと、

\begin{align}
\ k&=\frac{2}{d}\\
\ y&=ehe^{-k(x-d)-e^{-k(x-d)}}
\end{align}\\

上り坂（緑線）は

y=\frac{h}{d}x

下り坂（青線）は

\begin{align}
開始からピーク：ピークから終息&=\frac{1}{e}: 1-\frac{1}{e}\\
&=1:e-1\\
\end{align}\\

\begin{align}
\ y&=-\frac{h}{(e-1)d}x+h+\frac{h}{e-1}\\
\ &\fallingdotseq -\frac{0.58h}{d}x+1.58h\\
\end{align}\\

この波における総感染者数 G_max は三角形の面積に等しく

\begin{align}
\ G_{max}&=\frac{edh}{2}\\
\ &\fallingdotseq 1.36dh\\
\end{align}\\

2本の一次関数と総感染者数が「開始からピークまでの日数: d」と「ピーク時発生数: h」の2つの値から算出できます。

途中経過から総感染者数と終息日を予測する

ある地域で、以下のような経過になったとします。

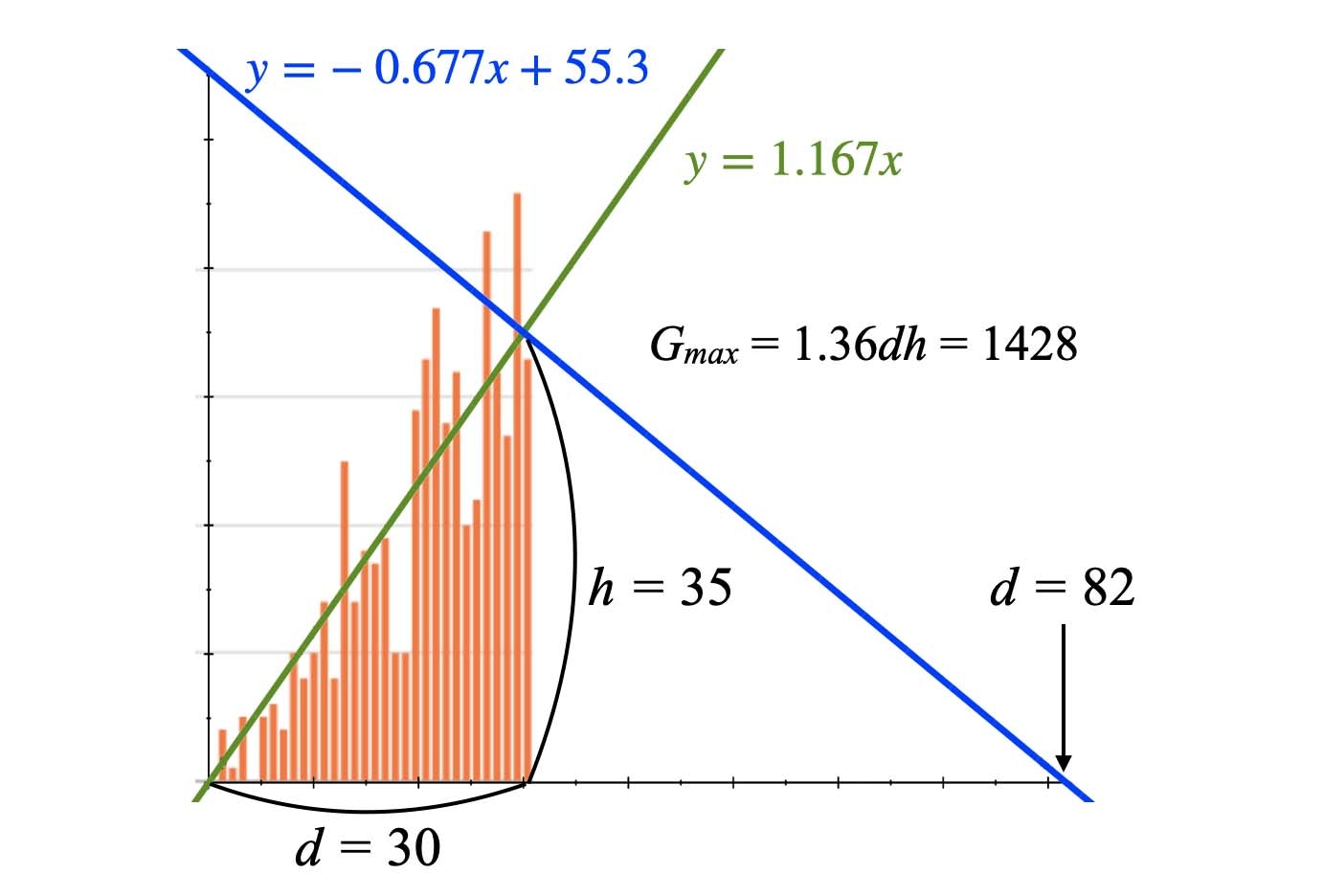
30日目に35人の新規発生数となり、この時点をピークとすると G_max = 1.36 dh = 1428人となります。30 e = 82日目に終息することが予測されます。もちろん、この先さらに増え続けてピークが後ろにずれ込む可能性はあります。また日本の第3波のように複数のゴンペルツ曲線が重なる可能性もあります。そのため、この1428人という数字は「順調にピークアウトして最も総感染者数が少なかった場合」の想定となります。この想定される総感染者数が地域の医療キャパシティを超える場合は医療崩壊の恐れあり、ということになります。

ゴンペルツ曲線とは何か？（13）

新型コロナ新規発生数を一次関数で近似する。

途中経過から総感染者数と終息日を予測する