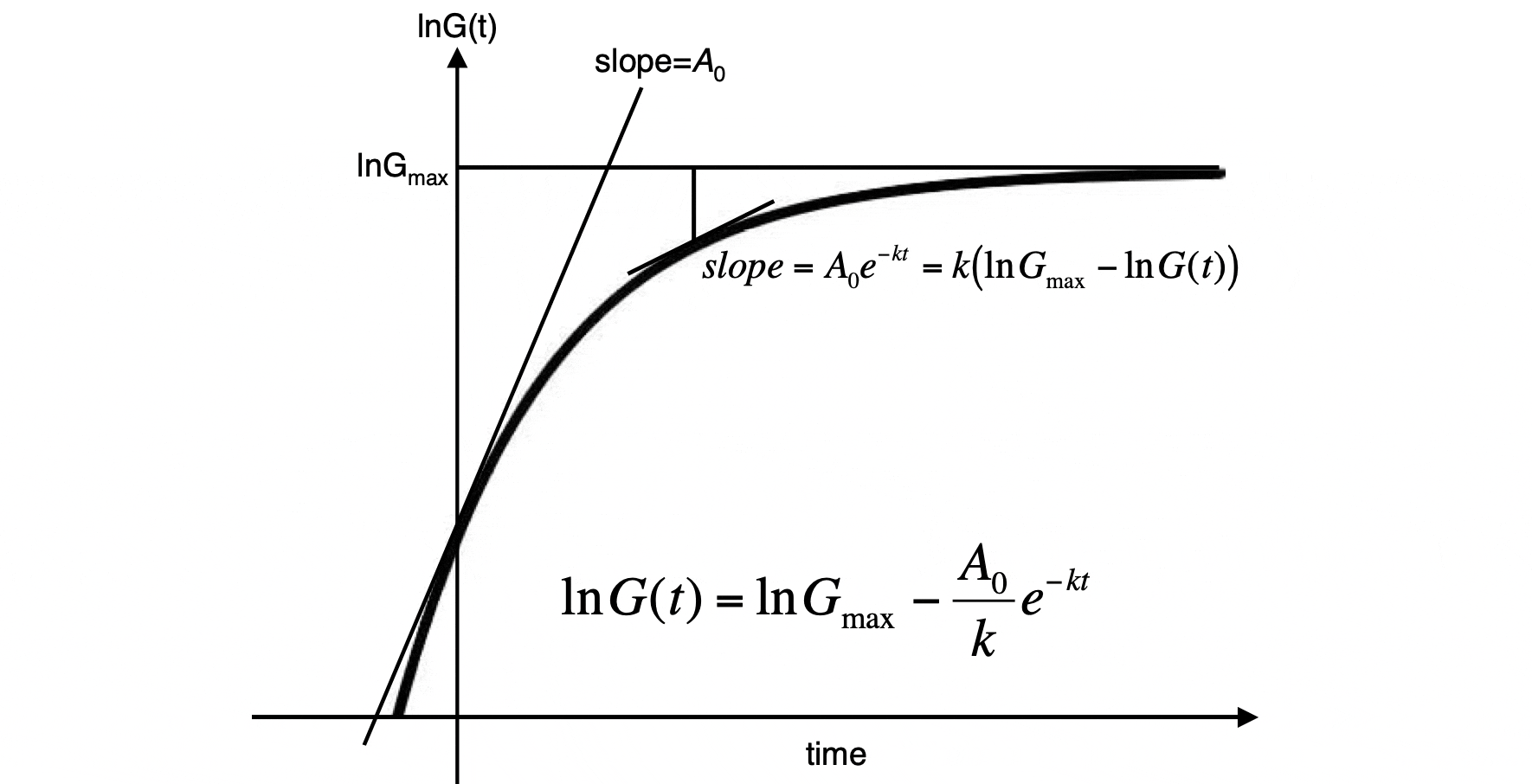ゴンペルツ曲線とは何か？（2） #数理モデル

前回のあらすじ

指数関数的増加・減少では対数グラフが直線化すること。
同一集団の人口を観察すると対数グラフの下方向の傾きが経時的に急峻になる（半減期が短縮する）こと。
$\ F(t)=\ln{G_{max}}-\frac{A_0}{k}e^{kt}$ で表せること。

を示しました。

生物の増殖曲線への応用

1825年に Gompertz が原著を発表してから100年後の1926年に Gompertz の理論が生物の増殖曲線に応用できることが発見されました¹。ウシの胎児が子宮内で成長する時の重量を対数化すると、下図のような等比級数的変化を示していたのです。
この図では t=∞ の時に有限の最大値に収束します。

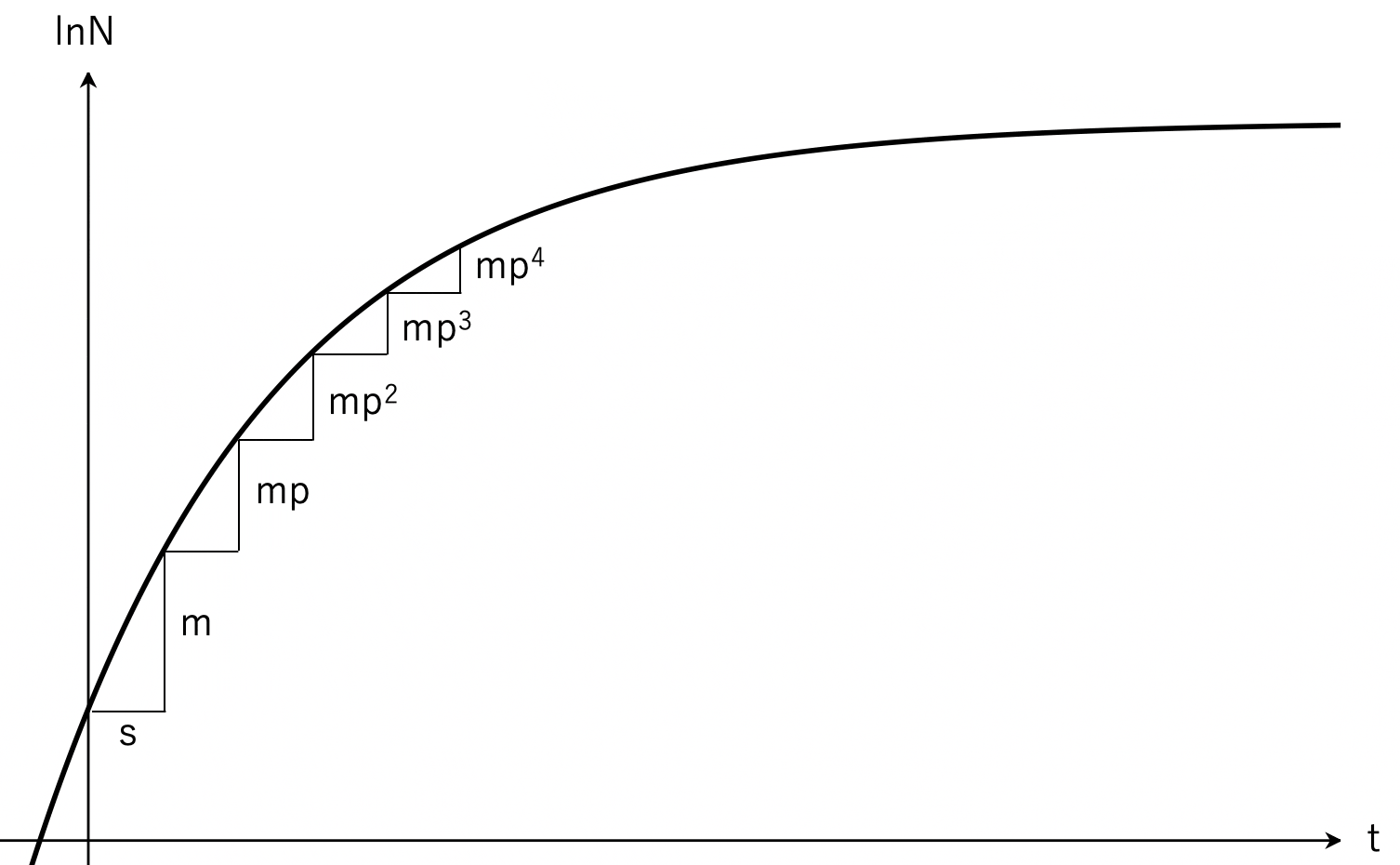
式で表すと Gompertz 元式の $\ e^{kt}$ が $\ e^{-kt}$ に置き換わり

\ F(t)=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}

対数化する前の数を $\ G(t)$ として、

\ F(t)=\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}

としても良いでしょう。
さて、上式を微分して得られる傾き

\frac{dF}{dt}=A_0e^{-kt}

より、
$\ t=0$ の時の傾き　$\ A_0$ が時間の経過と共に $\ e^{-kt}$ 倍に減衰することが分かります。
また、上式を変形すると曲線の傾きは、

\frac{dF}{dt}=A_0e^{-kt}=k\bigl(\ln{G_{max}}-\ln{G(t)}\bigr)

と表せます。

※対数化しないグラフでは、よく見るS字状の Gompertz 曲線となり、

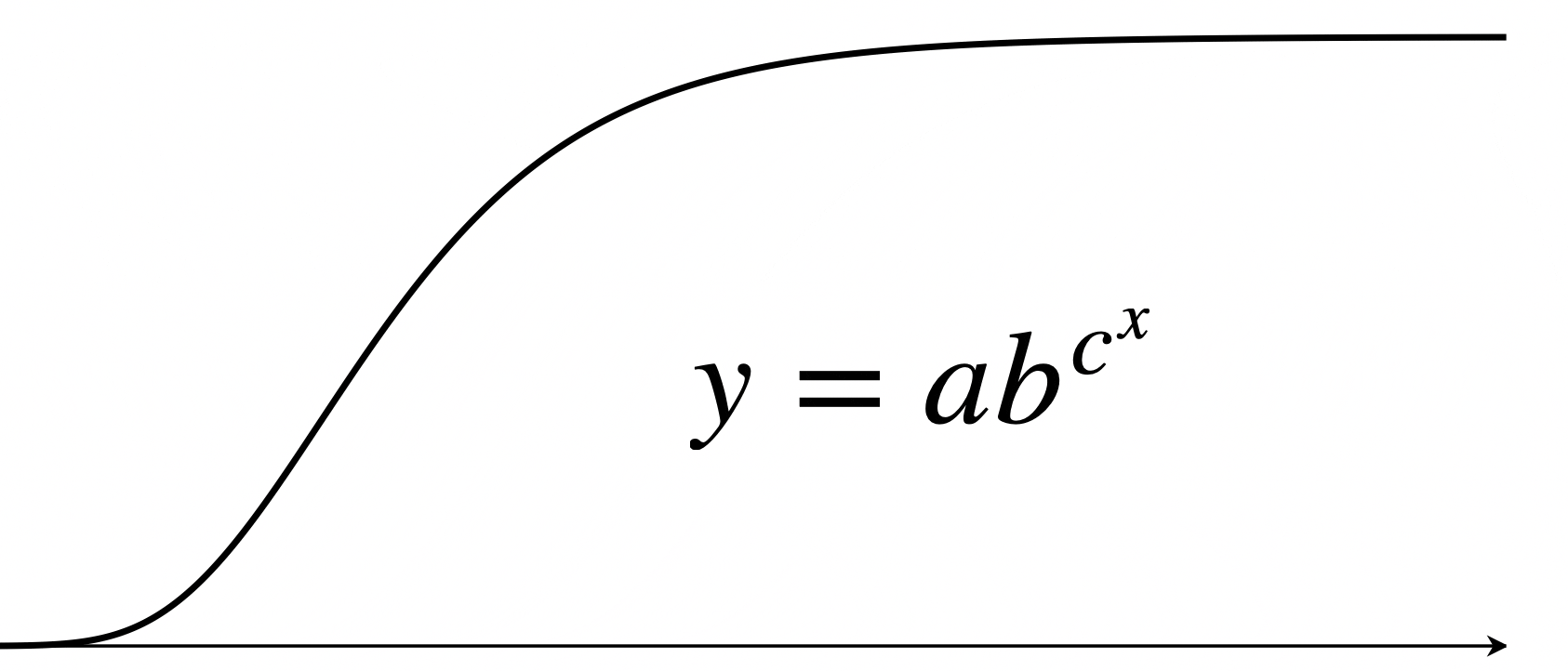
\ y=ab^{c^x}

と表せます。

\ y=G(t)\hspace{0.5mm},\hspace{1mm}a=G_{max}\hspace{0.5mm},\hspace{1mm}b=e^{-\frac{A_0}{k}}\hspace{0.5mm},\hspace{1mm}c=e^{-k}\hspace{0.5mm},\hspace{1mm}x=t

をそれぞれ代入することによって得られます。

ゴンペルツ曲線で、なぜ累積バグ数が表せるのか？

Gompertz 曲線は、ウシの胎児の子宮内成長曲線だけでなく、全ての生物の成長曲線に適用できる²と言われています。生物の成長曲線の他には、微量の DNA や RNA を増幅する方法（ポリメラーゼ・チェイン・リアクション法：PCR法）による template の増加も S字状を描き、Gompertz 曲線に従うことが報告されています³。PCR法では、サーマルサイクラーの周期に従って指数関数的に template が増加する (exponential growth) はずですが、検査試薬や容器の容量に上限があるため Gompertz 効果（経時的な doubling time の延長からやがてプラトーに達する）が現れるのでしょう。このように「ある倍加時間に伴って指数関数的に増加するが、ある有限の最大値があるために対数表示した時の傾きが時間 t と共に $\ e^{-kt}$ 倍に減衰する」ものは Gompertz 曲線に従い、累積バグ数にもそのような特性があるのでしょう。

補足：PCR法の原理（2021.1.26）

微量のDNAを増幅するPCR法の原理は下図の通りです。サーマルサイクラーという周期的に加熱・冷却を繰り返す装置を使用します。高熱で二本鎖DNAを分離させた後、冷却してプライマーをDNAに結合させます。伸長反応を起こさせた後、再び高熱で分離させて同じことを繰り返します。理論上はサーマルサイクラーの周期と厳密に等しい doubling time によって n サイクルで 2ⁿ 倍になる（指数関数的増加）はずです。

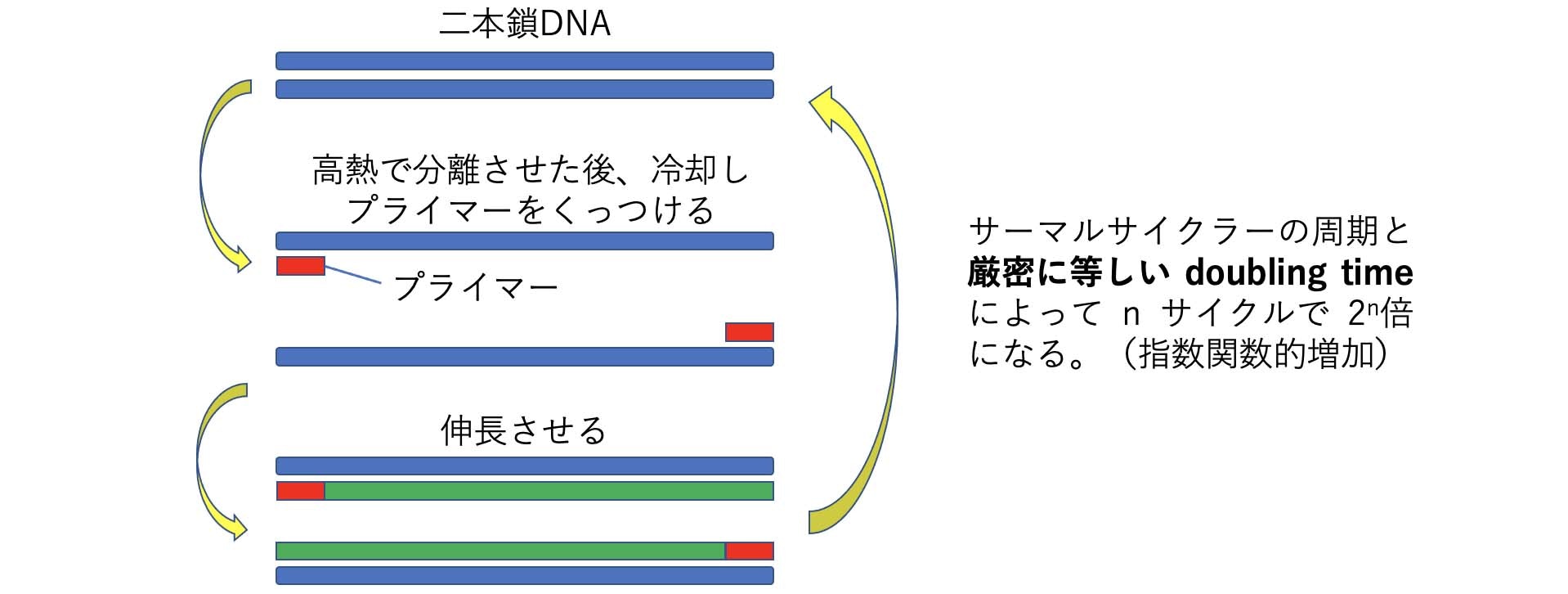
しかし、実際のPCR産物は以下に示すようなS字状のゴンペルツ曲線（二重指数関数）になります。

リソースが有限な現実世界では、指数関数的に増えようとするものでもゴンペルツ効果が働くのです。ゴンペルツ曲線は・人口統計学・情報工学・医学・生理学等の広範な領域で利用されています。

Wright, Sewall, book review in Jour. Am. Stat. Assoc., 21, 494, 1926. ↩
Laird AK. Dynamics of growth in tumors and in normal organisms. Natl Cancer Inst Monogr 1969; 30:15-28. ↩
Schlereth W, Bassukas ID, Deubel W, Lorenz R, Hempel K. Use of the recursion formula of the Gompertz function for the quantitation of PCR-amplified templates. Int J Mol Med. 1998;1:463-467. ↩