ゴンペルツ曲線とは何か？（3） #数理モデル

実測値は Gompertz 曲線に当てはまるか？

実測値が Gompertz 曲線に当てはまるか、を検証する方法を示します。

週数	累積発生数
1週	70
2週	670
3週	2600
4週	6000
5週	10000
6週	13500
7週	16500

上記のような結果が得られたとします。
グラフにすると以下のようになります。

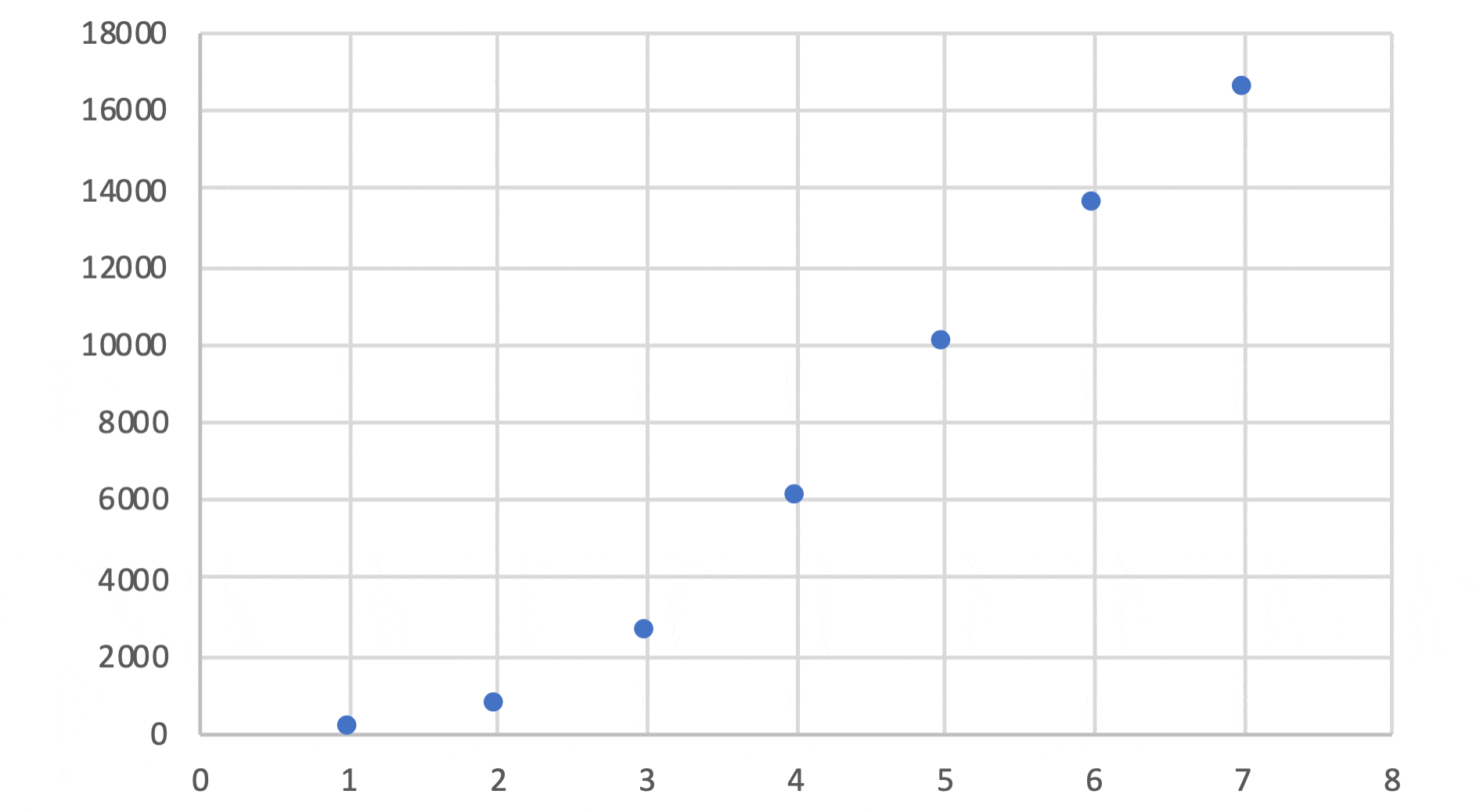
まだ、S字曲線になっていないような・・・。
果たして、7週までのデータは Gompertz 曲線に当てはまるのでしょうか？

累積発生数を対数化した値を $\ F(t)$ とし、任意の時間間隔を s とします。
Gompertz 曲線では、以下の式が成り立ちます。

\ F(t+s)=a+bF(t)

$\ F(t+s)$ は切片 a、傾き b の $\ F(t)$ の一次関数となります。

証明

\ F(t)=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}\\
\begin{align}
\ F(t+s)&=\ln{G_{max}}-\frac{A_0}{k}e^{-k(t+s)}\\
&=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}e^{-ks}\\
&=\ e^{-ks}\ln{G_{max}}-e^{-ks}\ln{G_{max}}+\ln{G_{max}}-\frac{A_0}{k}e^{-kt}e^{-ks}\\
&=\ e^{-ks}\bigl(\ln{G_{max}}-\frac{A_0}{k}e^{-kt}\bigr)+(1-e^{-ks})\ln{G_{max}}\\
\end{align}

$\ e^{-ks}=b$ 、$\ (1-e^{-ks})\ln{G_{max}}=a$ と定数で置き換えることができるので、

\therefore F(t+s)=a+bF(t)

上記データを対数化すると

週数	ln(累積発生数 )
1週	4.25
2週	6.51
3週	7.86
4週	8.70
5週	9.21
6週	9.51
7週	9.71

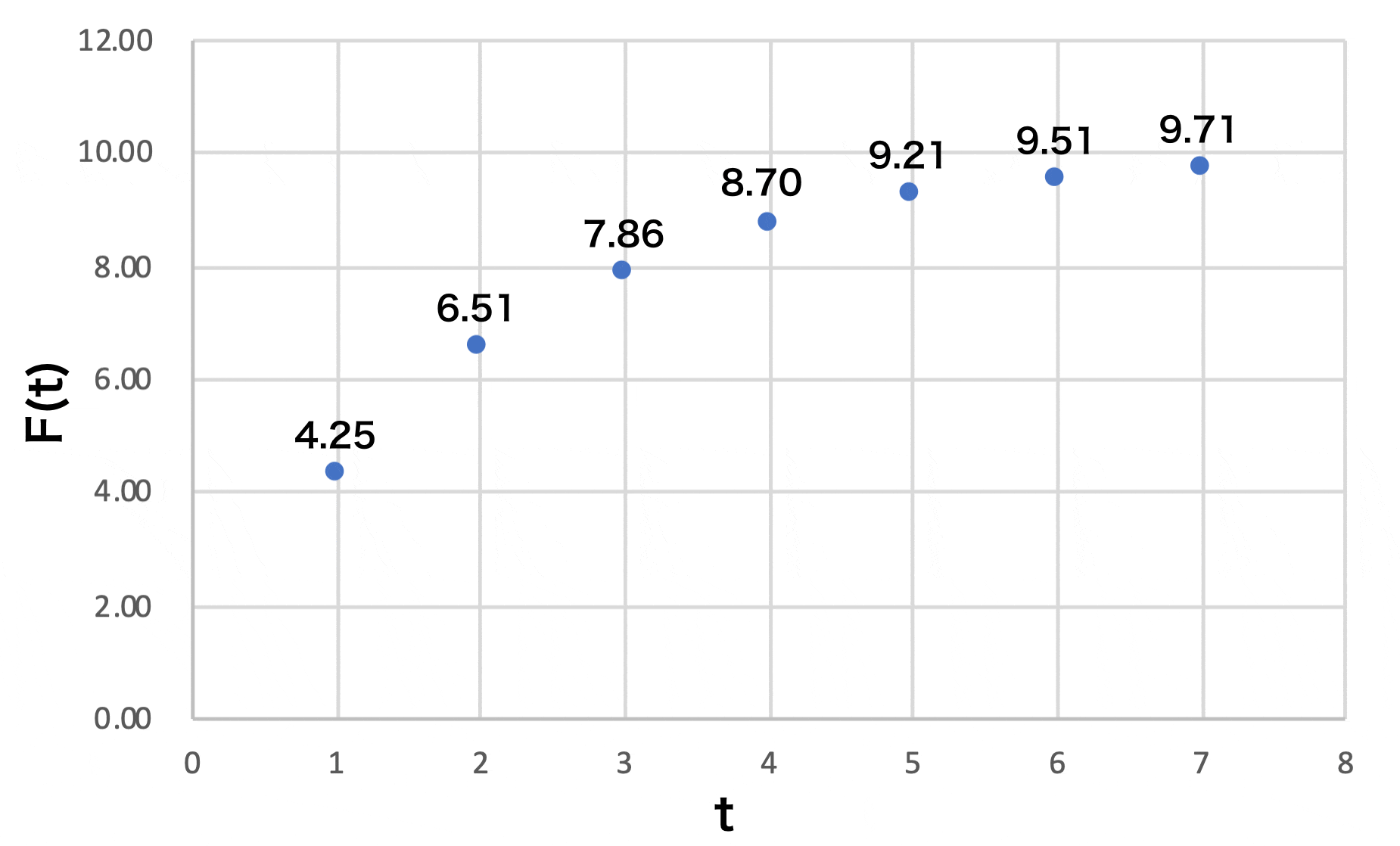
F(t)=4.25 の時、F(t+1)=6.51
F(t)=6.51 の時、F(t+1)=7.86
X軸をF(t), Y軸をF(t+1)としてプロットすると

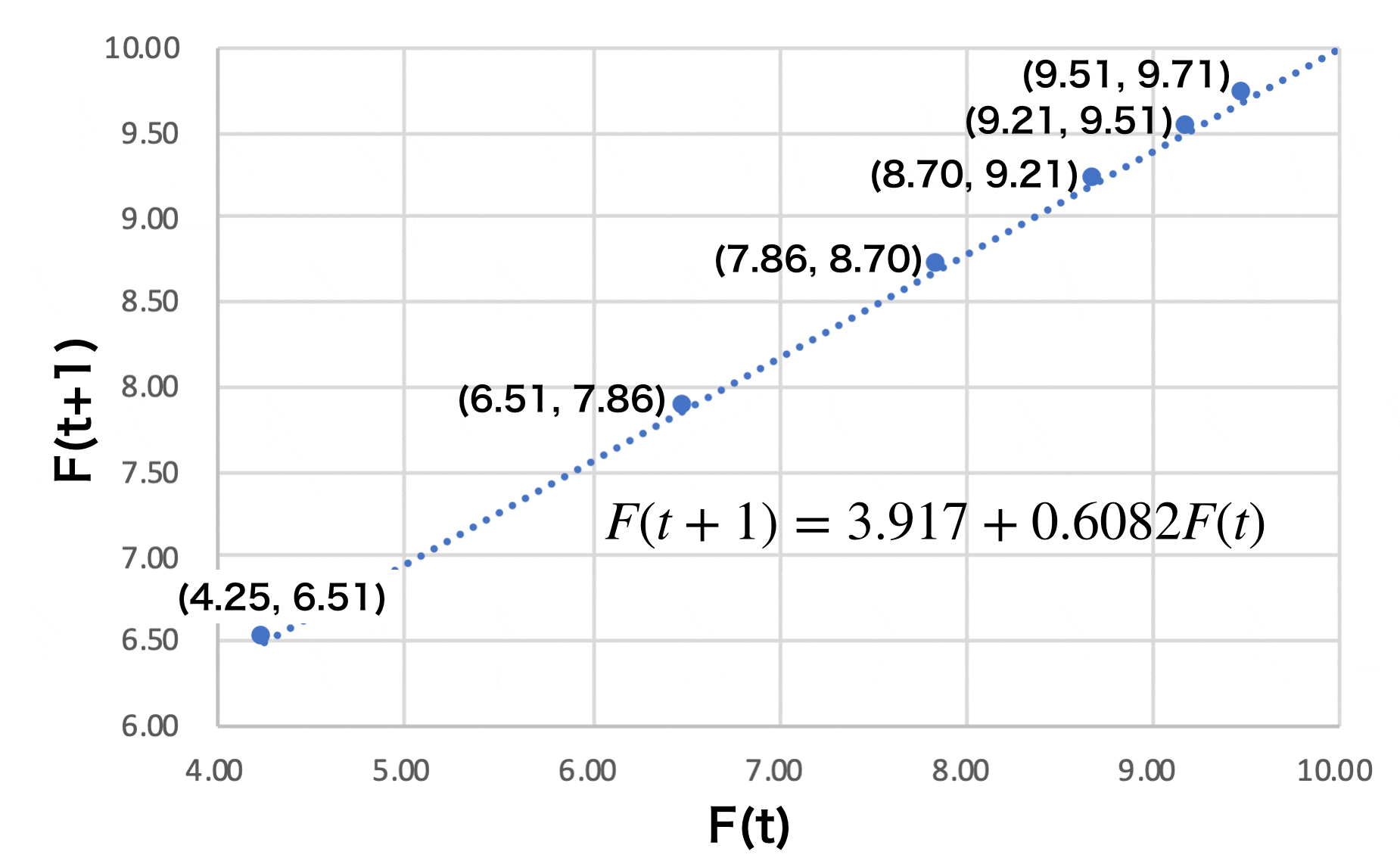
見事に直線化し、F(t+1) = 3.917 + 0.6082 F(t) の関係が成り立つことが分かりました。
$\ F(t+s) = a + bF(t)$ に当てはめると s = 1, a = 3.917, b = 0.6082
$\ e^{-ks}=b$ より

\ -ks=\ln b\\
\ k = -\frac {1}{s}\ln b\\
\ k=-\ln0.6082=0.5

$\ (1-e^{-ks})\ln{G_{max}}=a$ より

\ln{G_{max}}=\frac{a}{1-e^{-ks}}=\frac{a}{1-b}\\
\ln{G_{max}}=\frac{3.917}{1-0.6082}=10.0\\
\ G_{max}=e^{10.0}=22026

累積発生数の最大値は 22026 であることが分かりました。

次に $\ F(t)=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}$ の $\ A_0$ （最初の傾き）を求めましょう。
t=0 の時の傾きを求めることはできないので、F(1) = 4.25 の時の傾きを $\ A_0$ として、これを開始時点(t=0)とする式を作り、X軸方向に +1 平行移動するという方法をとります。

\ F(t)=\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}\\
\frac{dF}{dt}=A_0e^{-kt}\\
\ A_0e^{-kt}=k\bigl(\ln{G_{max}}-\ln{G(t)}\bigr)\\
\ A_0=0.5(10.0-4.25)=2.875\\
\frac{A_0}{k}=\frac{2.875}{0.5}=5.75

1週目を開始時点とした式は、$\ F(t)=\ 10.0-\ 5.75e^{-0.5t}$
X軸方向に +1 平行移動させて、
$\ F(t)=\ 10.0-\ 5.75e^{-0.5(t-1)}$ が求める式となります。

等間隔の3つの値から ln G_max を求める方法

X軸をF(t), Y軸をF(t+s)としてプロットすると
$\ F(t+s) = a + bF(t)$ の関係（切片 a、傾き b の直線）が成り立ちました。
この直線は以下の1, 2, 3週の値だけで求められます。

週数	ln(累積発生数)
1週	4.25
2週	6.51
3週	7.86

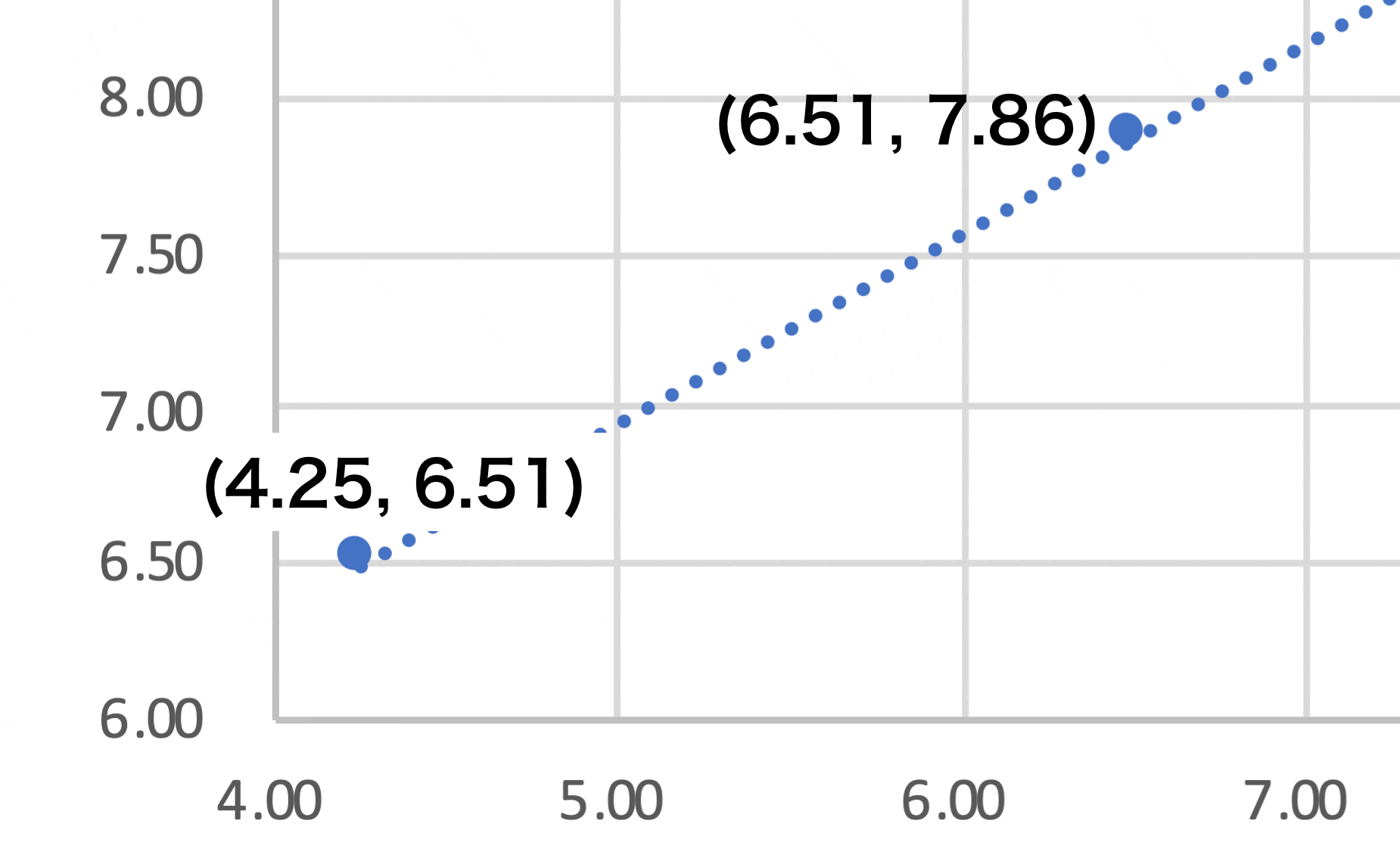
A = 4.25, B = 6.51, C = 7.86 とすると
座標(A, B) と (B, C) を通る直線を求めれば良いのです。

傾き b は、

\ b=\frac{C-B}{B-A}

切片 a は、
$\ F(t+s) = a + bF(t)$ より、
$\ a = F(t+s) - bF(t)$
$\ F(t) = A, F(t+s) = B$ を代入すると、

\begin{align}
\ a&=B-bA\\
&=B-\frac{C-B}{B-A}A\\
&=\frac{B^2-AC}{B-A}\\
\end{align}

$\ (1-e^{-ks})\ln{G_{max}}=a$ より

\begin{align}
\ln{G_{max}}&=\frac{a}{1-e^{-ks}}\\
&=\frac{a}{1-b}\\
&=\frac{\frac{B^2-AC}{B-A}}{1-\frac{C-B}{B-A}}\\
&=\frac{AC-B^2}{A-2B+C}
\end{align}

A = 4.25, B = 6.51, C = 7.86 より

\ln{G_{max}}=9.86\\
\ G_{max}=e^{9.86}=19149

A, B, C の値は、等間隔の3点ならどれを使っても良く、

週数	ln(累積発生数)
2週	6.51
4週	8.70
6週	9.51

では

\ln{G_{max}}=9.99\\
\ G_{max}=e^{9.99}=21807

週数	ln(累積発生数)
1週	4.25
4週	8.70
7週	9.71

では

\ln{G_{max}}=10.01\\ 
\ G_{max}=e^{10.01}=22248

と概ね 2万に近い値になります。

まとめ

測定値が Gompertz 曲線に従う時、対数化した値を F(t) 、等しい時間間隔を s とすると F(t+s) が F(t)の一次関数となる。
等しい時間間隔の 3つの ln(累積発生数)をA, B, C とすると、$\ln{G_{max}}=\frac{AC-B^2}{A-2B+C} $ が成り立つ。

ゴンペルツ曲線とは何か？（3）

実測値は Gompertz 曲線に当てはまるか？

等間隔の3つの値から ln Gmax を求める方法

まとめ

等間隔の3つの値から ln G_max を求める方法