医学・生理学への応用
1個の癌細胞が1cm大になるのに何年かかるか?
さて、1個の癌細胞が1cm大になるのに何年かかるでしょうか?
一説では5~6年と言われています。
この仮説は腫瘍細胞の doubling time(倍加時間)が常に一定であるという前提に基づいています。
通常、臨床家が目にする腫瘍の doubling time は2ヶ月程度です。
1cmの腫瘍には10億個(2の30乗個)の細胞が含まれ、1個の癌細胞が30回分裂すれば(2の30乗)で10億個になります。
だから 1個が10億個になるのに2ヶ月x30回=60ヶ月=5~6年という計算になります。
しかし「腫瘍細胞の doubling time は常に一定である」という前提は正しいでしょうか?
実は腫瘍細胞は Gompertz 曲線に従って増殖する事が知られています。Gompertz 曲線では細胞数が少ないときは doubling time が短く、細胞数が多くなると doubling time が延長するという特徴があります。
子宮内の胎児の成長も Gompertz 曲線に従います。
1個の受精卵は1日で2個に分裂します。(doubling time 1日)
一方 1500グラムの胎児が3000グラムに倍増するには2ヶ月かかります。(doubling time 2ヶ月)
もし胎児の成長の doubling time が最初から最後まで2ヶ月であったなら、1個の受精卵が1cmになるまでに5年かかってしまいます!(そんなことは有り得ませんね)
実際は 1個の受精卵はわずか1ヶ月で1cm大(10億個)まで増殖します。つまり、受精卵の doublig time は最初は短いですが、それ以降どんどん延長していくのです。
腫瘍細胞も胎児の成長と同様 Gompertz 曲線に従うので、1個の癌細胞が1cm大になるまでの期間は一般に言われているよりずっと短いと思われます。
C型肝炎ウイルスと Gompertz 曲線
私は 2008年に「Gompertzian model を用いた HCV 動態の解析」1と題する試論を発表しました。これは「C型肝炎ウイルス(HCV)の増殖が Gompertz 曲線に従い、インターフェロン(IFN)による HCV の崩壊が指数関数的(exponential decay)であるならば、HCV の減少曲線はどうなるか?」を考案したものです。
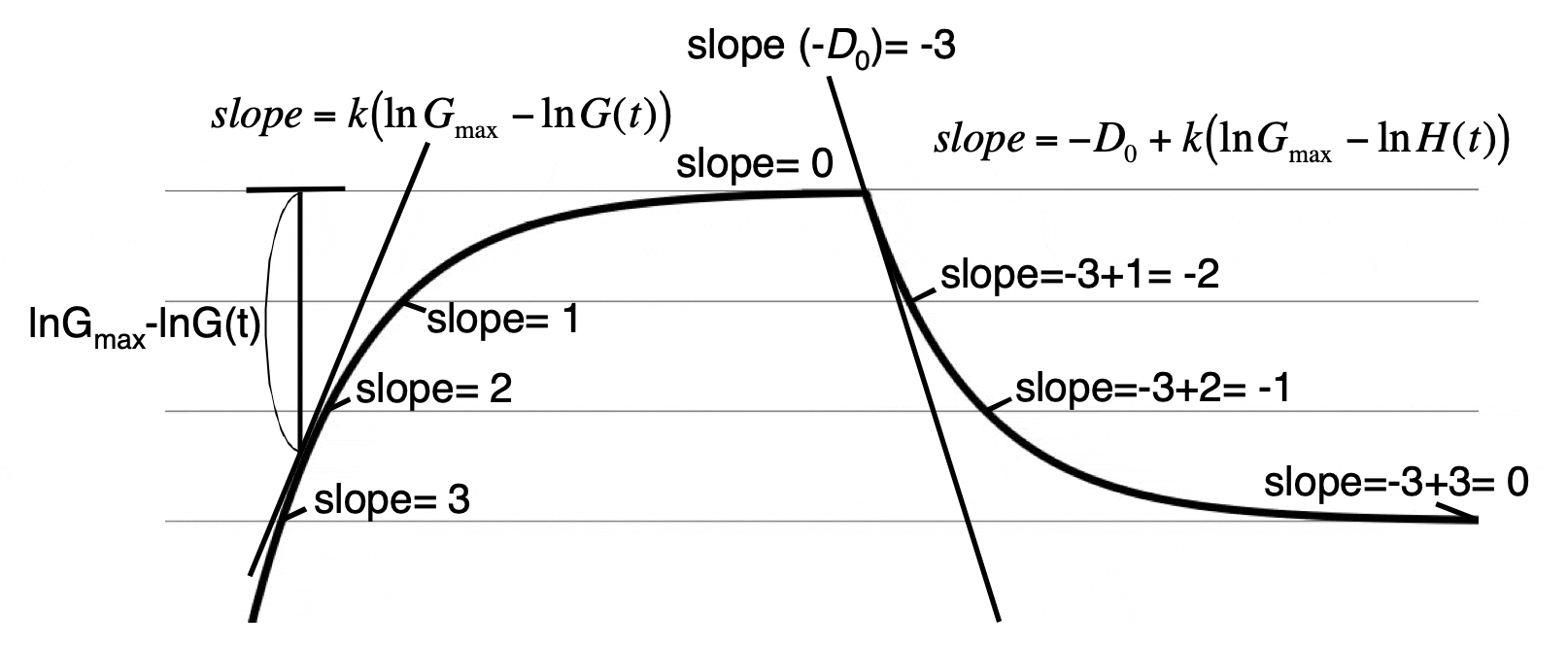
上図のように HCV が Gompertz 曲線に従って人体で増殖し、ある有限の最大値 $\ln{G_{max}} $ で定常状態になっているとします。
IFN による HCV の崩壊が指数関数的であるとして、傾き $\ -D_0=-3$ の下向きの直線を描くとします。ここで我々は Gompertz 効果を考慮に入れなければいけません。HCV は $\ln{G_{max}} $ に近づくにつれて増殖曲線の傾きが減衰して、定常状態ではこれ以上増えないようになっています。しかし IFN で HCV が減少すると再び上向きの増殖しようとする力が働くのです。上図のてっぺんの直線 $\ln{G_{max}} $ から3目盛下方では HCV が増殖しようとする上向きの傾きが +3 で IFN による下向きの傾きが -3 となり -3+3=0 で平衡状態となります。
IFN 投与下の対数化された HCV 数を $\ln{H(t)} $ とすると HCV の上向きに増殖しようとする力は $\ln{G_{max}} $ と $\ln{H(t)} $ の差に比例し、$\ k\bigl(\ln{G_{max}}-\ln{H(t)}\bigr)$ と表せます。※ゴンペルツ曲線とは何か?(2)
$\ln{H(t)} $ の傾き $\frac{d\ln{H(t)}}{dt} $ は下向きの傾き $\ -D_0$ と上向きの傾き $\ k\bigl(\ln{G_{max}}-\ln{H(t)}\bigr)$ の和になるので、
\frac{d\ln{H(t)}}{dt}=-D_0+k\bigl(\ln{G_{max}}-\ln{H(t)}\bigr)
という微分方程式ができます。
これを以下のように解いてみましょう。
\ -D_0+k\bigl(\ln{G_{max}}-\ln{H(t)}\bigr)=Z
とします。
両辺を時間 t で微分すると
\ -k\frac{d\ln{H(t)}}{dt}=\frac{dZ}{dt}
$\frac{d\ln{H(t)}}{dt}=Z $ なので
\frac{dZ}{dt}=-kZ\\
\int\frac{1}{Z}dZ = -k\int dt\\
\ln{Z}=-kt+c\\
\ Z=e^{-kt+c}=e^ce^{-kt}\\
\frac{d\ln{H(t)}}{dt}=e^ce^{-kt}\\
t = 0 の時、傾きは $\ -D_0$ なので $\ e^c=-D_0$ となり
\frac{d\ln{H(t)}}{dt}=-D_0e^{-kt}\\
\ -D_0e^{-kt}=-D_0+k\bigl(\ln{G_{max}}-\ln{H(t)}\bigr)\\
\therefore\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}
実測値は上式に当てはまるか?
任意の時間間隔を s とすると、以下の式が成り立ちます。
\ln{H(t+s)}=a+b\ln{H(t)}
$\ln{H(t+s)}$ は切片 a、傾き b の $\ln{H(t)}$ の一次関数となります。
証明
\ln{H(t)}=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}\\
\begin{align}
\ln{H(t+s)}&=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-k(t+s)}\\
&=\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-ks}e^{-kt}\\
&=\ e^{-ks}\bigl(\ln{G_{max}}-\frac{D_0}{k}\bigr)-e^{-ks}\bigl(\ln{G_{max}}-\frac{D_0}{k}\bigr)+\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-ks}e^{-kt}\\
&=\ e^{-ks}\bigl(\ln{G_{max}}-\frac{D_0}{k}+\frac{D_0}{k}e^{-kt}\bigr)+(1-e^{-ks})\bigl(\ln{G_{max}}-\frac{D_0}{k}\bigr)\\
\end{align}
$\ e^{-ks}=b$ 、$\ (1-e^{-ks})\bigl(\ln{G_{max}}-\frac{D_0}{k}\bigr)=a$ と定数で置き換えることができるので、
\therefore \ln{H(t+s)}=a+b\ln{H(t)}
Forestier らはC型肝炎の患者に抗ウイルス薬 Telaprevir(VX950)を投与してから数日間のウイルス量の減少を詳細に記載しています。2以下(左図)は、Hepatology 2007;46:640―648 の論文から抜粋した HCV の減少曲線を方眼紙に書き写したものです。
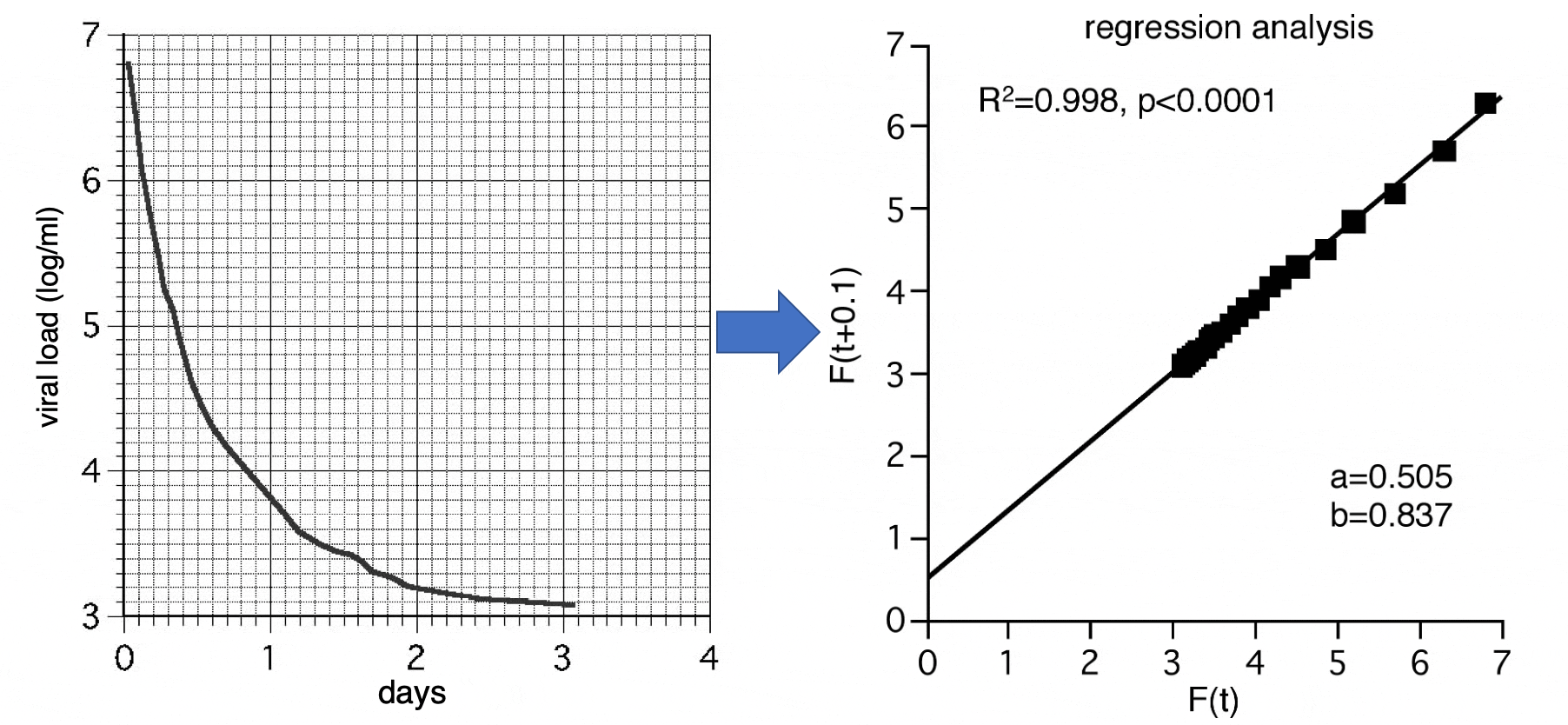
この曲線を縦軸 F(t+0.1)、横軸 F(t)としてプロットし直すと(右図)、傾き b、切片 a の直線になります。回帰分析では、相関係数 $\ R^2=0.998\hspace{0.5mm},\hspace{1mm}p<0.0001 $であり、数式と実測値は極めて正確に一致していることが分かります。
ゴンペルツ曲線とは何か?(1)
ゴンペルツ曲線とは何か?(2)
ゴンペルツ曲線とは何か?(3)
ゴンペルツ曲線とは何か?(5)
ゴンペルツ曲線とは何か?(6)
ゴンペルツ曲線とは何か?(7)
ゴンペルツ曲線とは何か?(8)
ゴンペルツ曲線とは何か?(9)
ゴンペルツ曲線とは何か?(10)
ゴンペルツ曲線とは何か?(11)
ゴンペルツ曲線とは何か?(12)
ゴンペルツ曲線とは何か?(13)
ゴンペルツ曲線とは何か?(14)