More than 3 years have passed since last update.

ゴンペルツ曲線とは何か？（6）

Last updated at 2021-06-20Posted at 2020-03-08

##新型コロナウイルス (COVID-19) の累積患者数は Gompertz 曲線に従うか？
ジョンズ・ホプキンス大学のサイトで COVID-19 の累積患者数が発表されています。
中国の患者数はS字状を描いており、Gompertz 曲線が適用できるかもしれません。
ゴンペルツ曲線とは何か？（3）で実測値が Gompertz 曲線に当てはまるかを検証する方法を示しています。高価な統計ソフトがなくてもエクセルで簡単にできます。

時間(t)における COVID-19 の累積患者数を G(t)、対数化したものを ln G(t)とし Gompertz 曲線に従う時

\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}

と表せます。
任意の時間間隔を s とすると対数化された Gompertz 曲線では、以下の式が成り立ちます。

\ F(t+s)=a+bF(t)

$\ F(t+s)$ は切片 a、傾き b の $\ F(t)$ の一次関数となります。
以下は 2020/1/24~2020/3/7 の中国の累積 COVID-19 発生数です。

date	G(t)	lnG(t)
2020/1/24	916	6.82001636
2020/1/25	2000	7.60090246
2020/1/26	2700	7.90100705
2020/1/27	4400	8.38935982
~~	中略	~~
2020/3/4	80300	11.2935249
2020/3/5	80400	11.2947695
2020/3/6	80600	11.2972539
2020/3/7	80700	11.2984939

エクセルの工程を以下に図示します。

ln G(t) の列の隣に ln G(t+1) の列を作ります。
2020/1/25 以降の ln G(t) の値をコピーして2020/1/24のセルの隣で右クリックし「形式を選択してペースト -> 値」を選択します。
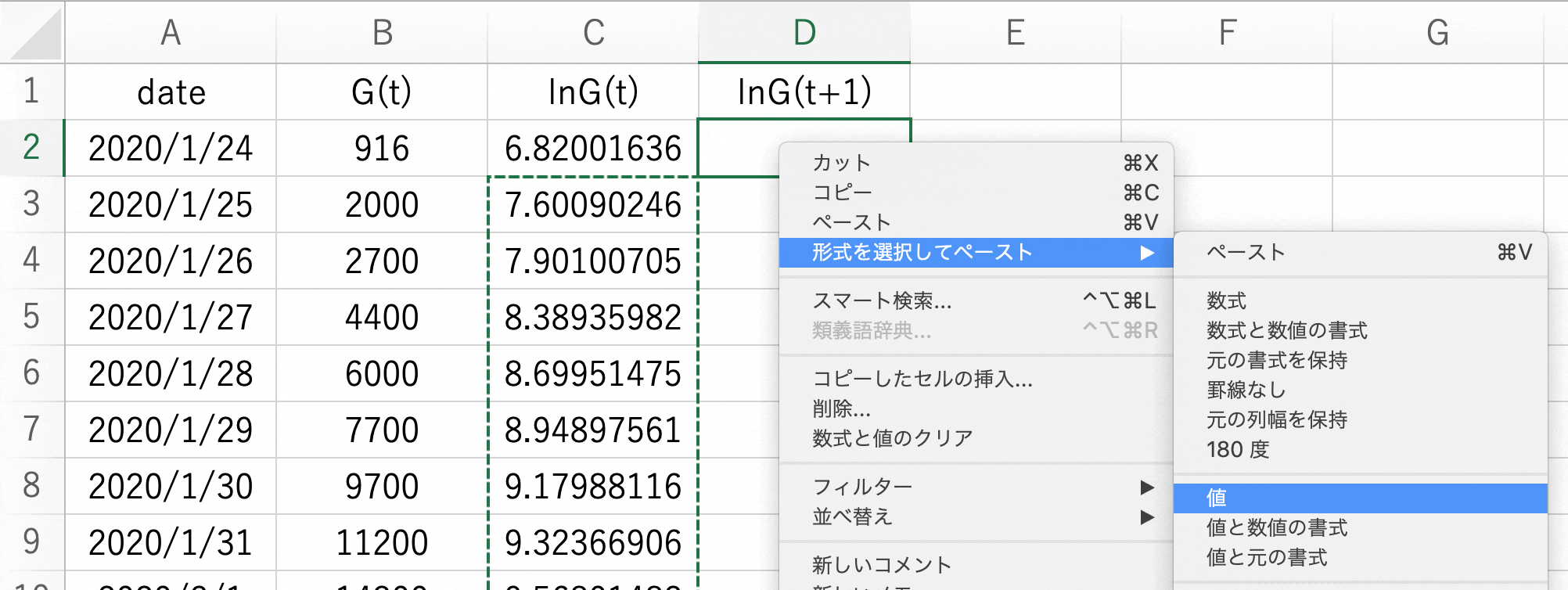
ln G(t) と ln G(t+1) のデータを選択し「挿入 -> 散布図」をクリックします。
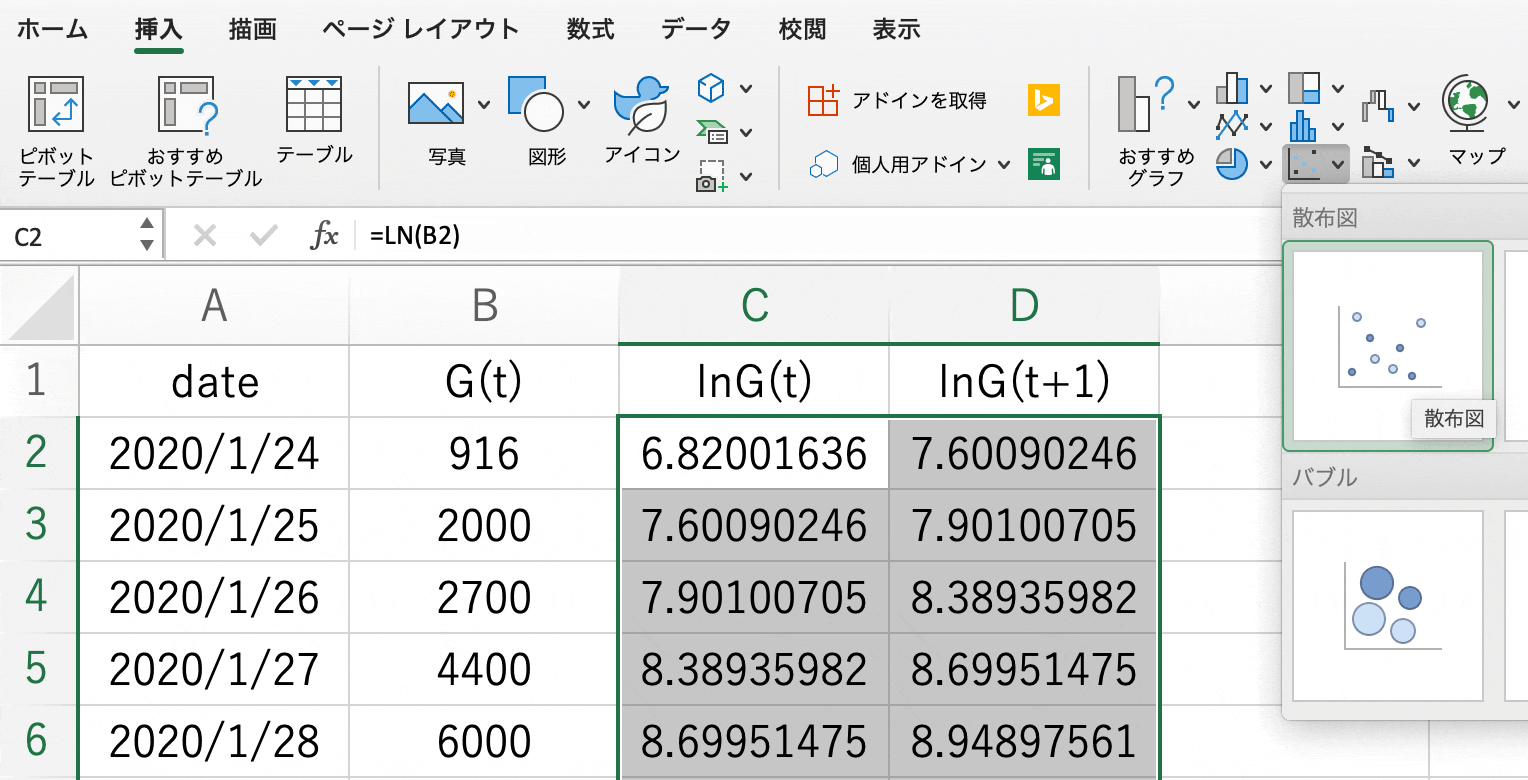
できた散布図を右クリックし「近似曲線の追加… -> 線形近似」を選択します。

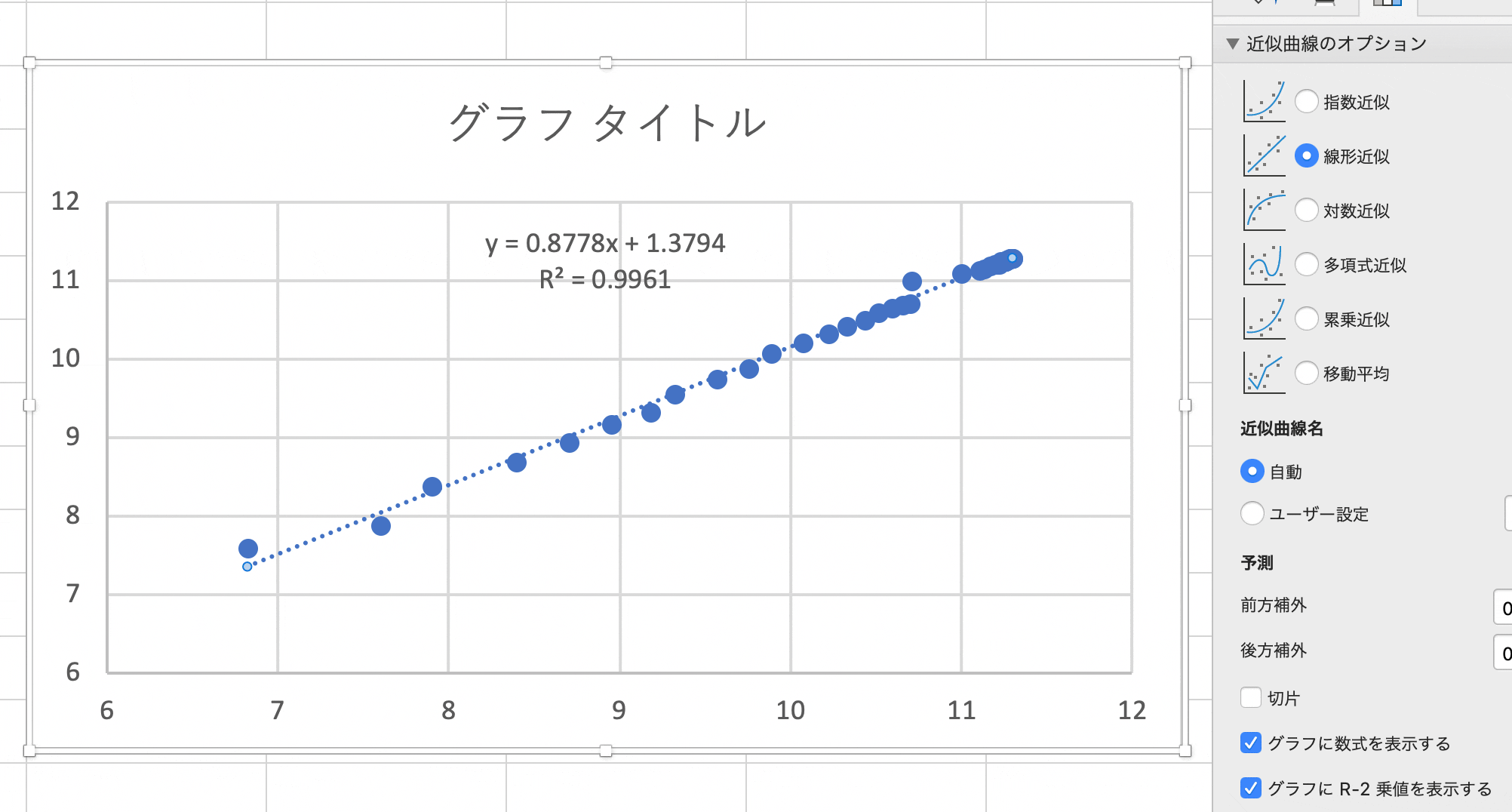
切片 1.3794、傾き 0.8778 できれいに直線化しています。(R² = 0.9961)
##最大値 G_max を求める。
F(t+s) = a + b•F(t) に当てはめると s = 1, a = 1.3794, b = 0.8778
ゴンペルツ曲線とは何か？（3）より

\ (1-e^{-ks})\ln{G_{max}}=a\\
\begin{align}
\ln{G_{max}}&=\frac{a}{1-e^{-ks}}\\
&=\frac{a}{1-b}\\
&=\frac{1.3794}{1-0.8778}=11.2880524\\
\end{align}\\
\ G_{max}=e^{11.2880524}=79862

累積発生数の最大値は 79862 であることが分かりました。
実測値が80000を超えているので、ほぼ上限に達していることが推測されます。
※中国で診断基準が改定された 2020/2/14 以降のデータに限定すると、
a = 1.8452, b = 0.8367 となり $\ G_{max}=80777$ となります。
###等しい時間間隔の3値から求める方法
等しい時間間隔の 3つの ln(累積発生数)を A, B, C とすると、

\ln{G_{max}}=\frac{AC-B^2}{A-2B+C}

の関係が成り立つので、

date	lnG(t)
2020/2/16	11.1619485
2020/2/26	11.2657453
2020/3/7	11.2984939

の3値（時間間隔 10日）から計算すると G_max = 81927 となります。
##A₀/k を求める
$\ e^{-ks}=b$ より

\ -ks=\ln b\\
\begin{align}
\ k &= -\frac {1}{s}\ln b\\
&=-\ln 0.8778=0.1303365
\end{align}

\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}\\
\frac{A_0}{k}e^{-kt}=\ln{G_{max}}-\ln{G(t)}\\
\frac{A_0}{k}=\frac{\ln{G_{max}}-\ln{G(t)}}{e^{-kt}}

2020/1/24 を t = 0 として、近似直線から外れてなさそうなポイント（t = 10, ln G(t) = 9.88837391)を代入してみましょう。

\begin{align}
\frac{A_0}{k}&=\frac{\ln{G_{max}}-\ln{G(t)}}{e^{-kt}}\\
&=\frac{11.2880524-9.88837391}{e^{-0.1303365\times10}}\\
&=5.15314679
\end{align}

求める式は、

\ln{G(t)}=11.2880524-5.15314679e^{-0.1303365t}\\
\ G(t)=e^{11.2880524-5.15314679e^{-0.1303365t}}

となりました。
実測値と計算値を重ね合わせてみると

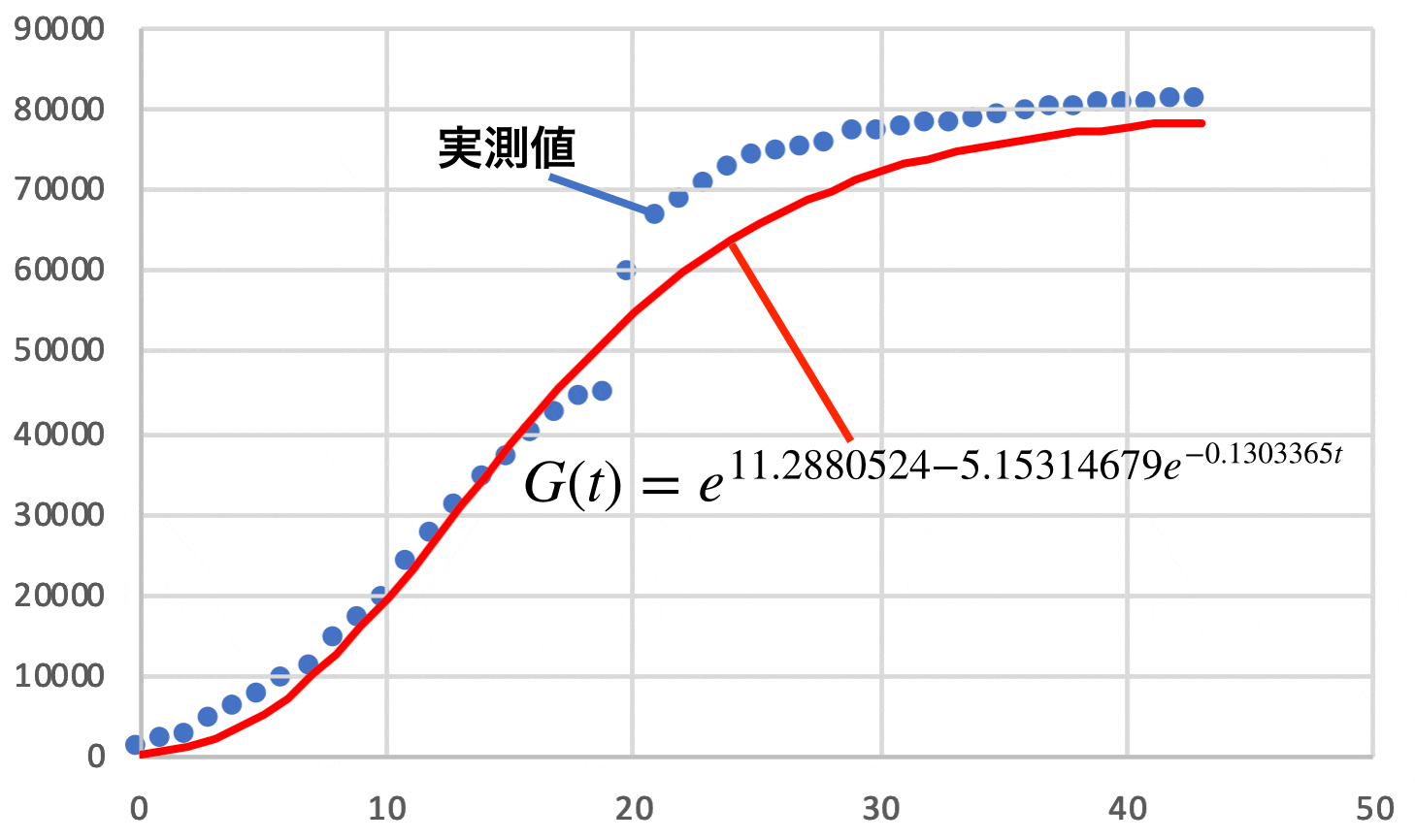
・・・実測値と計算値の間に若干のズレがあります。
##iPhone アプリ「Gompertz 曲線計算機」
私は10年前の2010年に「Gompertz 曲線計算機」という iPhone アプリ（無料）を公開しました。このアプリは任意の3点の時間と値を入力すると、その3点を通る Gompertz 曲線を計算できます。

day	G(t)
4	6000
22	68300
43	80700
これらの値を入力したところ、

\ G_{max}=81301\\
\ln{G(t)}=11.3058-2.6064e^{-0.1503(t-4)}\\
\ G(t)=81301\times0.0738^{e^{-0.1503(t-4)}}

という結果が得られました。

・・・かなりよく近似しています。
次章（7）では Excel 版 Gompertz 曲線計算機をご紹介致します。
##まとめ

（中国の）COVID-19 の累積患者数は概ね Gompertz 曲線に従う。
中国の患者数は収束されつつある。
エクセルで比較的簡単に Gompertz 曲線を作ることができる。
「Gompertz 曲線計算機」で更に正確に近似できる。

##追記　米国の COVID-19 発生数に Gompertz 曲線は当てはまるか (2020.5.30)
2020年4月15日〜5月27日までの米国のデータで検証します。

date	G(t)	lnG(t)
2020/4/15	636674	13.364013
2020/4/16	667981	13.412015
2020/4/17	700062	13.4589242
2020/4/18	728352	13.4985397
~~	中略	~~
2020/5/24	1643000	14.3120344
2020/5/25	1662000	14.3235323
2020/5/26	1681000	14.3348994
2020/5/27	1699000	14.3455504

前述の方法で、縦軸を ln G(t+1) 横軸を ln G(t) とする散布図を作ります。

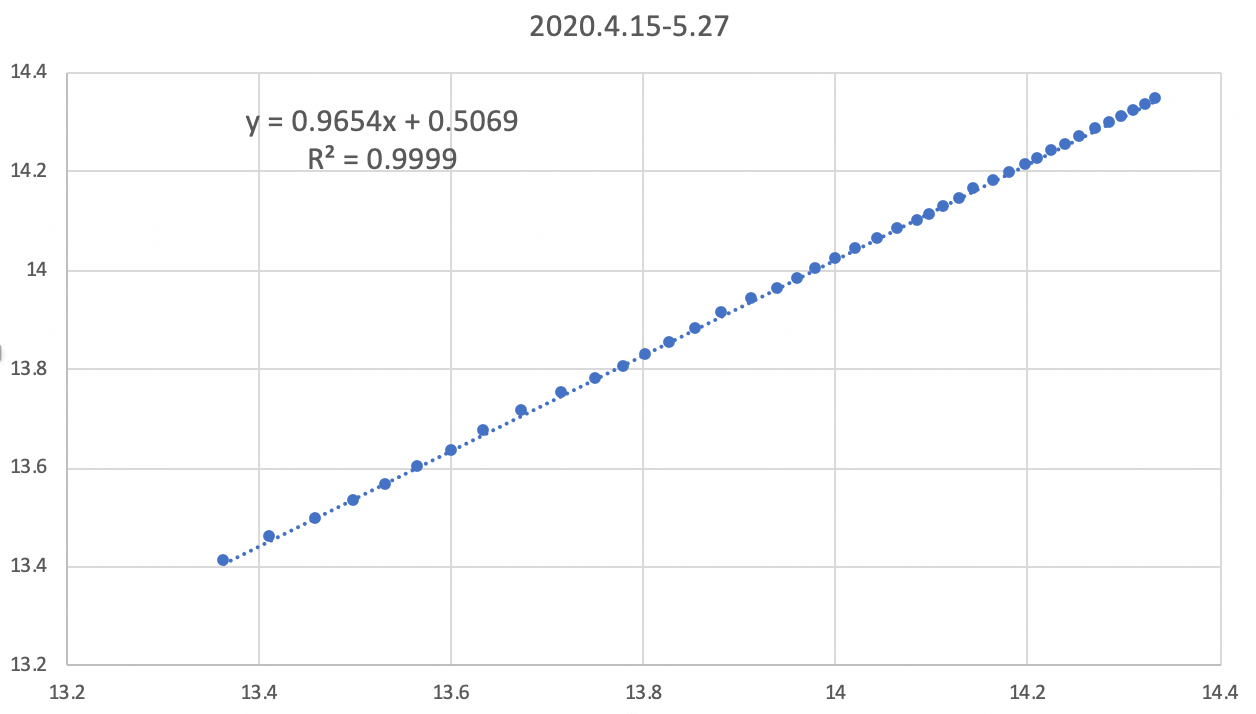
切片 0.5069、傾き 0.9654 で直線化しています。(R² = 0.9999)
ln G(t+s) = a + b•ln G(t) に当てはめると s = 1, a = 0.5069, b = 0.9654

\ (1-e^{-ks})\ln{G_{max}}=a\\
\begin{align}
\ln{G_{max}}&=\frac{a}{1-e^{-ks}}\\
&=\frac{a}{1-b}\\
&=\frac{0.5069}{1-0.9654}=14.650289\\
\end{align}\\
\ G_{max}=e^{14.650289}=2304303

最大値は 230万となります。
iPhone アプリ「Gompertz 曲線計算機」を使ってみると、

day	G(t)
2020年4月15日	636674
2020年5月5日	1204000
2020年5月27日	1699000

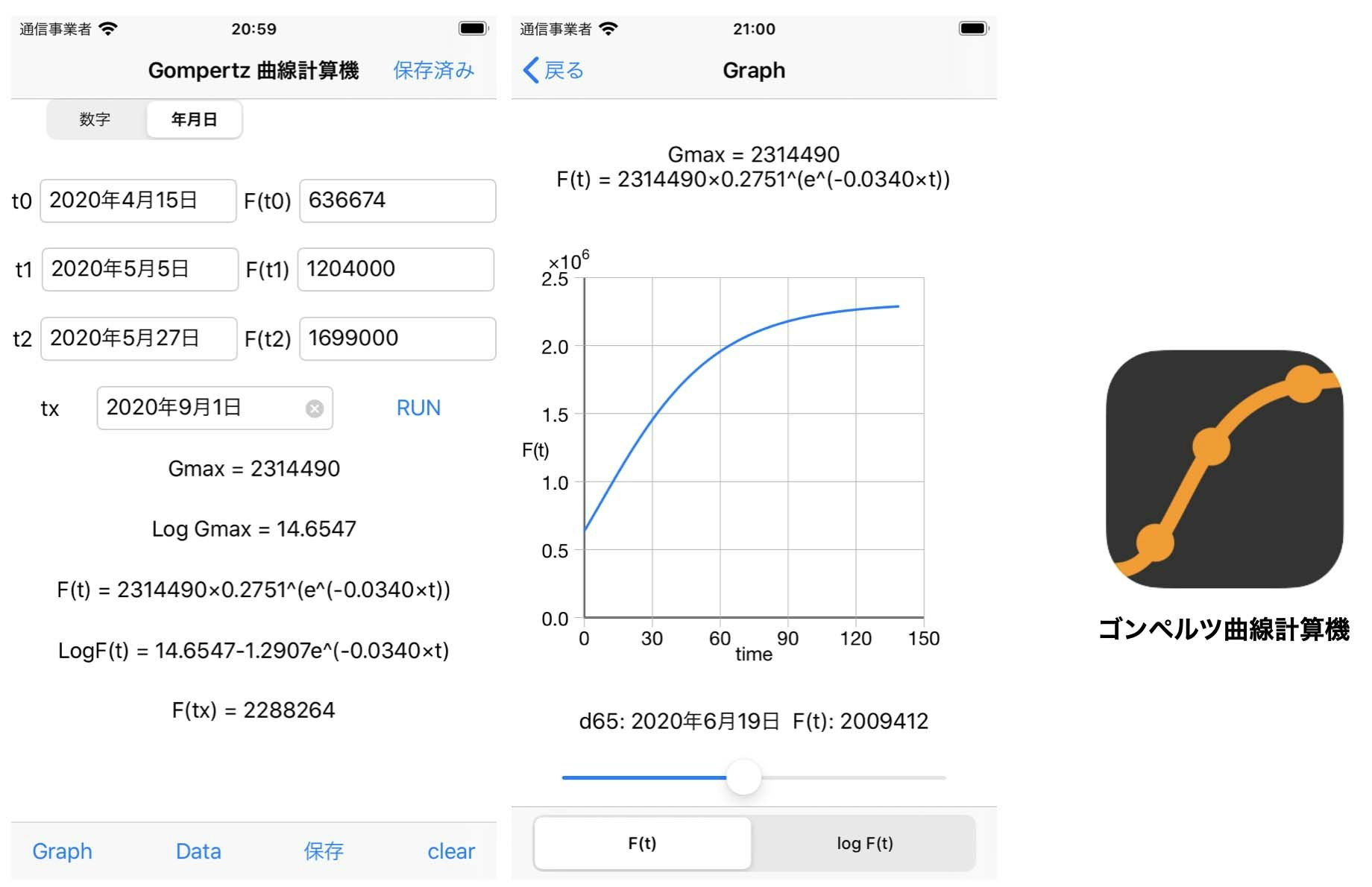計算値と実測値の相関係数は 0.9998 でした。
減衰係数 k = 0.0340 より対数表示した時の曲線の傾きが1日で e^-0.0340 倍（= 0.9665倍）に減衰します。G_max = 2314490 でした。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up