「K値による予測を使うべきでない理由」へのコメント #COVID-19

K値による予測を使うべきでない理由

先日、東京海洋大学准教授　勝川俊雄先生が
K値による予測を使うべきでない理由
と題して御自身の公式サイトに投稿されました。

内容の要約は以下の通りです。

K値による COVID-19 感染者数予測は、実際にはゴンペルツ曲線である。
世界各国の感染者推移をみるとゴンペルツ曲線に近い挙動を示すこともあるが、当てはまらないことも多い。
過去のデータから導いたゴンペルツ曲線が現在始まりつつある第二波にも当てはまるとは限らない。
仮に第二波がゴンペルツ曲線に従うとしても、流行初期のノイズの多いデータからピークを推測することはできない。（わずかなパラメータの差は、初期の傾きは重なってもピーク値に大きな違いを生じさせる。）
ゴンペルツの減衰係数は人間社会の行動変容の影響を受けて変動するはずである。しかしメディアに「何もしなくても、勝手に新規感染者が減少する」という根拠のない楽観論が広がっている。

・・・勝川先生の御指摘は正しいと思います。

私は Qiita を通じて Gompertz 曲線を啓蒙しておりますので本稿でコメントさせて頂きます。

Gompertz 曲線のおさらい

ゴンペルツ曲線の式は

\ y=ab^{c^x}

と表せます。（二重指数関数）

\ y=G(t)　a=G_{max}　b=e^{-\frac{A_0}{k}}　c=e^{-k}　x=t

をそれぞれ代入して両辺を対数化すると

\ln{G(t)}=\ln{G_{max}}-\frac{A_0}{k}e^{-kt}

となります。G_max は最大値、A₀ は観測開始時の対数グラフの傾き、k は減衰係数、t は時間を表します。
対数化された Gompertz 曲線では傾き A₀ が時間の経過とともに e^-kt 倍に減衰します。

K値

K値は大阪大学教授　中野貴志先生が提唱された指標で、直近1週間の感染者数を累計感染者数で割ったものです。
K値とは何か？
上記のページに K値の発見に至る経緯が示されています。
累計感染者数が指数関数 N(d) = N₀e^Ad の時、対数化したグラフは上向きの直線になるはずです。中国の累計感染者数をみると傾きが徐々に緩やかになっており指数係数が変化していることがわかります。中野先生は適当な間隔の2点間の数の比を取って推移をみることから K値を発見されました。Benjamin Gompertz が200年前に、「死亡による人口減少を対数表示したら傾きが徐々に急峻になった」ことから Gompertz 曲線を発見したのと似ています。
K値理論では A(d+1) = kA(d) に従い、日々一定の割合で指数係数 A が 0（感染収束）に近づくと仮定されました。これは前述の「対数化された Gompertz 曲線では傾き A₀ が時間の経過とともに e^-kt 倍に減衰」と同義です。
東京工業大学教授　秋山泰先生は指数係数が一定減衰仮定を満たす時 K値の時間関数 K(t) が 1-（ゴンペルツ曲線）で表せることを証明されました。

G(t) をゴンペルツ関数として

\ G(t)=ab^{e^{-kt}}

と表せる時

\ K(t)=1-b^{e^{-kt}}

が成り立ちます。（0 < b < 1)
ゴンペルツ曲線は最大値と減衰係数 k が決まれば曲線の形状が1つに決まります。（x 軸方向の平行移動は生じますが）※そのため上式 K(t) は曲線の形状は正しいですが、x 軸方向に若干のずれ（平行移動）が生じています。0 ~ 1の範囲で b がどのような値になっても曲線の形状は一定です。
b を e に置き換えて以下のように一般化することも可能です。（この場合 e > 1 なので指数の係数にマイナス "–" をつけます。K(0) = 1-1/e を通る位置に平行移動しています。）

\ K(t)=1-e^{-e^{-kt}}

累計発生数の対数グラフの傾きが増大する場合は

\ K(t)=1-e^{-e^{kt}}

となり K(t) は上向きの曲線になります。（下図赤線参照）
興味深いことにゴンペルツ曲線の減衰係数 k は y 軸切片における K(t) の傾き K’(0)を -e 倍したものに等しくなります。
以下で K(t) を微分して K’(0) を求めます。

\begin{align}
\ K(t)&=1-e^{-e^{-kt}}\\
\ U=-e^{-kt}&,　V=-kt　とすると\\
\ K(t)&=1-e^U\\
\ U&=-e^V\\
\frac{dK}{dt}&=\frac{dK}{dU}\frac{dU}{dV}\frac{dV}{dt}\\
\frac{dK}{dU}&=-e^U\\
\frac{dU}{dV}&=-e^V\\
\frac{dV}{dt}&=-k\\
\frac{dK}{dt}&=-e^U(-e^V)(-k)\\
\ &=-ke^Ue^V\\
\ &=-ke^{-e^{-kt}}e^{-kt}\\
\ K'(0)&=-\frac{k}{e}\\
\therefore k&=-eK'(0)
\end{align}\\

下図において、K(0) = 1-1/e となり、変曲点（最も傾きが急峻な位置）となります。K'(0) の傾きが急峻な時は減衰や増大の度合いも急峻になります。

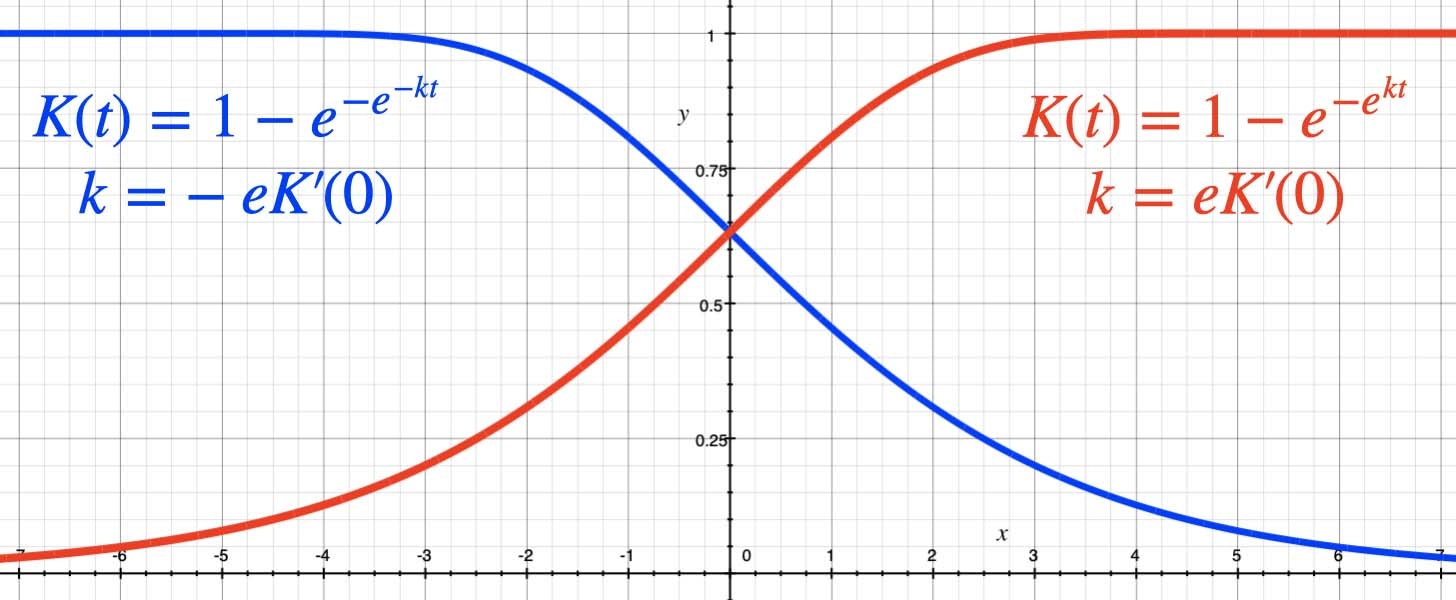
累計感染者数が指数関数に従う場合は K(t) は傾き 0 の定数となります。

Gompertz 曲線は未来予測に使えるか？

ゴンペルツ曲線とは何か？（6）で 2020年4月15日〜5月27日までの米国のデータから

\ F(t) = 2314490 \times 0.2751^{e^{-0.0340t}}

という式を導き G_max = 231万4490人と推測しました。
しかし 2020.7.19 の時点で米国の累計感染者数は 371万1835人で予測を大きく上回っています。ジョンズ・ホプキンス大学のサイトで対数グラフをみると2段階のゴンペルツ曲線に乗ったあとで傾きが更に増大しているようです。この傾向は日本にも当てはまります。これは指数係数の一定減衰仮定が当てはまらないことを意味します。勝川先生が指摘されるように人間社会の行動変容の影響で減衰の程度が変化するのでしょう。

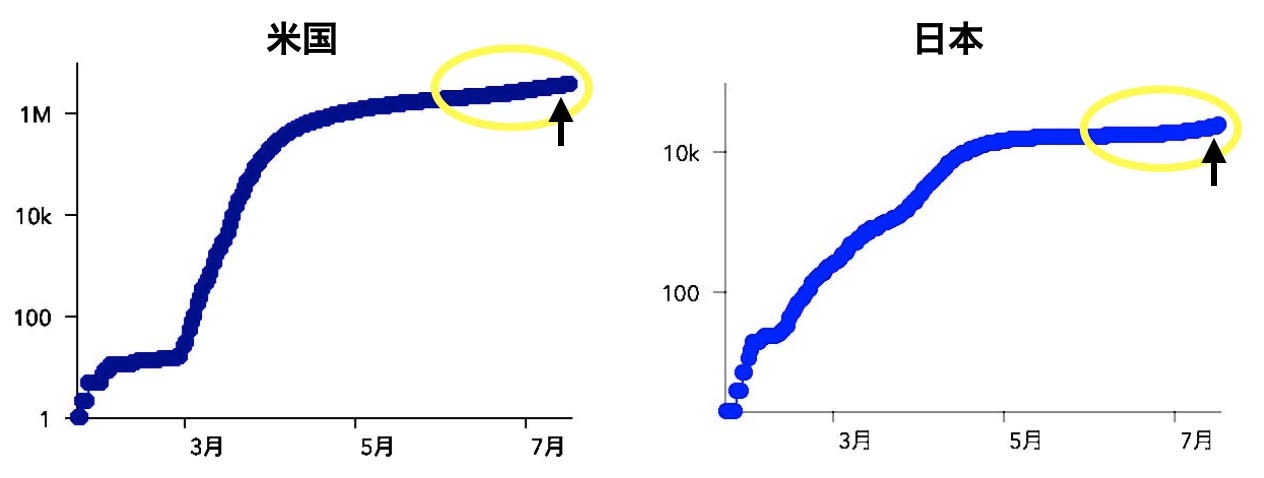
K値の有用性

中野貴志先生が Benjamin Gompertz 級のセレンディピティで発見された K値は、そのまま未来予測に使うには若干問題があるかもしれませんが非常に有用であると思います。
以下は米国のある時期における累計感染者数です。

day	累計感染者数
2020年3月23日	43900
2020年3月30日	162700
2020年4月6日	367200

2020年3月30日の K値は 0.73
2020年4月6日の K値は 0.56
一見、著しい増加に見えますが K値の傾きが負であることから減衰局面にあることがわかります。

day	累計感染者数
2020年6月13日	2075000
2020年6月20日	2255000
2020年6月27日	2510000

2020年6月20日の K値は 0.08
2020年6月27日の K値は 0.10
K値の傾きが正であることから指数関数を上回る増大局面（doubling time の短縮！）と言えます。大勢の人がマスクをせずにデモに参加していた時期と重なるのかもしれません。

Gompertz 曲線では等しい時間間隔の累計感染者数を対数化した値を A, B, C とすると

\ln{G_{max}}=\frac{AC-B^2}{A-2B+C}

の関係が成り立ちます。※ゴンペルツ曲線とは何か？（3）
2020年3月23日〜4月6日のデータから計算すると G_max = 139万6598 となります。この時点の減衰係数が維持できていれば、これくらいの累計感染者数で済んだことになります。2020年6月13日〜6月27日のデータでは G_min = 155万4163 を最小値として上方に拡散する結果になります。

このように K値を使えば直近2週間の累計感染者数から簡単な計算で現在のトレンドを知ることができます。更に K(t) の傾きを求めるだけでゴンペルツの減衰係数を導くことができます。（K(t) = 1-1/e の時の傾きなら -e 倍、K(t) = 0.5 の時の傾きなら -2.88倍する）また 0 < K(t) < 1 の範囲に必ず収まることもデータの扱いを容易にします。

おわりに

K値やゴンペルツ曲線を未来予測に使うには「現在の行動変容の強度が将来も不変である」という条件が必要です。
Gompertz という「神の見えざる手」によって「何もしなくても勝手に新規感染者が減少する」と考えるのは、勝川先生がおっしゃるように「根拠のない楽観論」だと思います。
K値はむしろ、現在のトレンドを解析して未来の行動変容を促すのに使えるのではないでしょうか。
発展途上の感染症数理モデルですが多くの人が知恵を絞って、より洗練されたものになればよいと思います。幸い日本は「~~高校で微分方程式を習う~~※」という欧米にはないアドバンテージ（Factor Xの1つ？）があり、この分野で世界をリードできるかもしれません
※現在は、高校で微分方程式を習わないそうです・・・。

補足：日本の第2波にゴンペルツ曲線と SIR モデルを当てはめる（2021.2.11）

日本の第2波に二重指数関数（ゴンペルツ曲線）を当てはめました。
参考：ゴンペルツ曲線とは何か？（10）
行動変容の指標として同時期の渋谷スクランブル交差点の人出¹も示します。

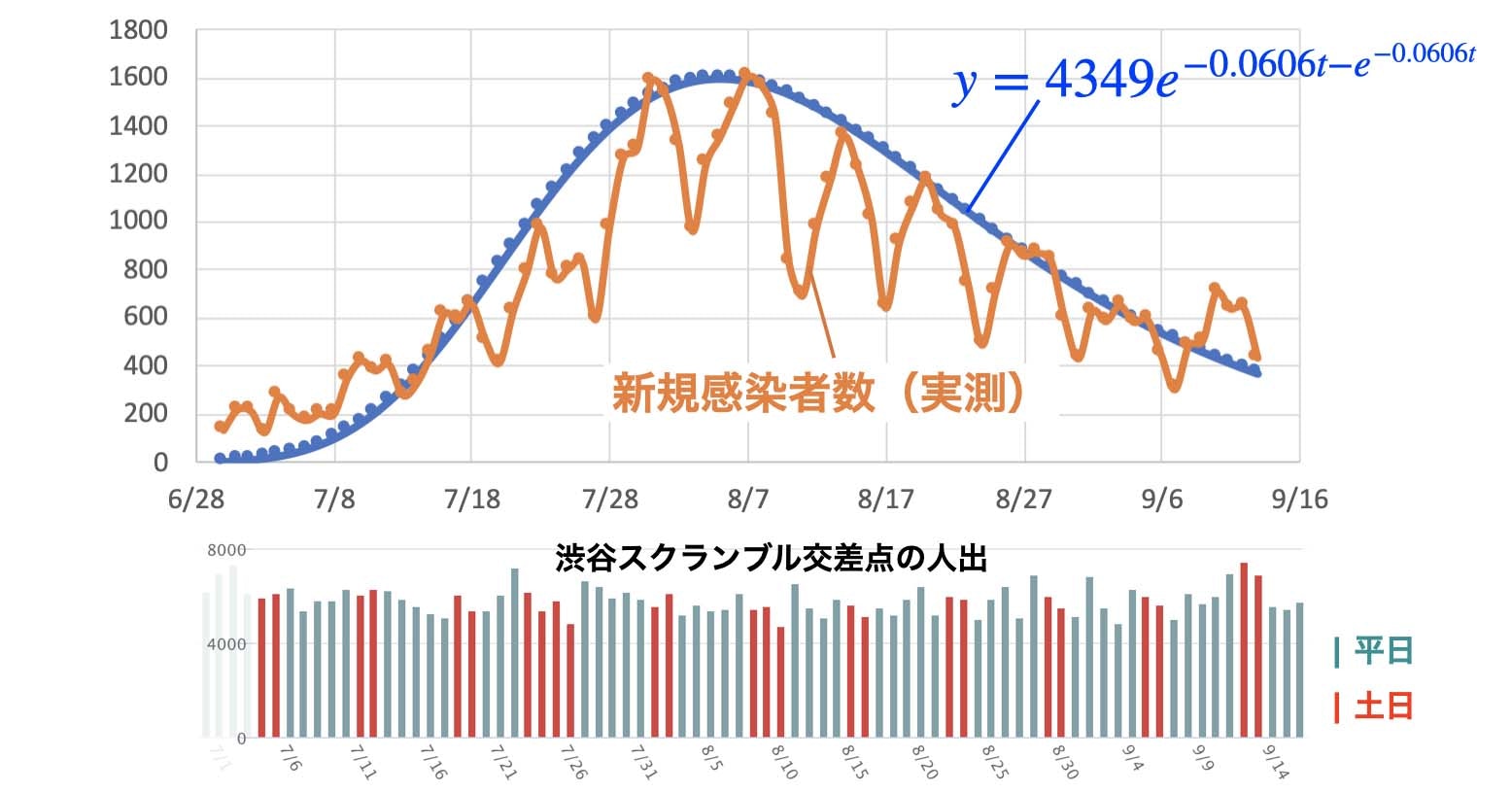
\ y=4349e^{-0.0606t-e^{-0.0606t}}\\

にて第2波の始まりから終息まで fit しています。ゴンペルツの減衰係数は 0.0606 と1つの値になります。経過中、渋谷スクランブル交差点の人出に変化がなかったことから行動変容の強度は一定であったと思われます。
指数関数（SIRモデル）を当てはめると下図のようになります。

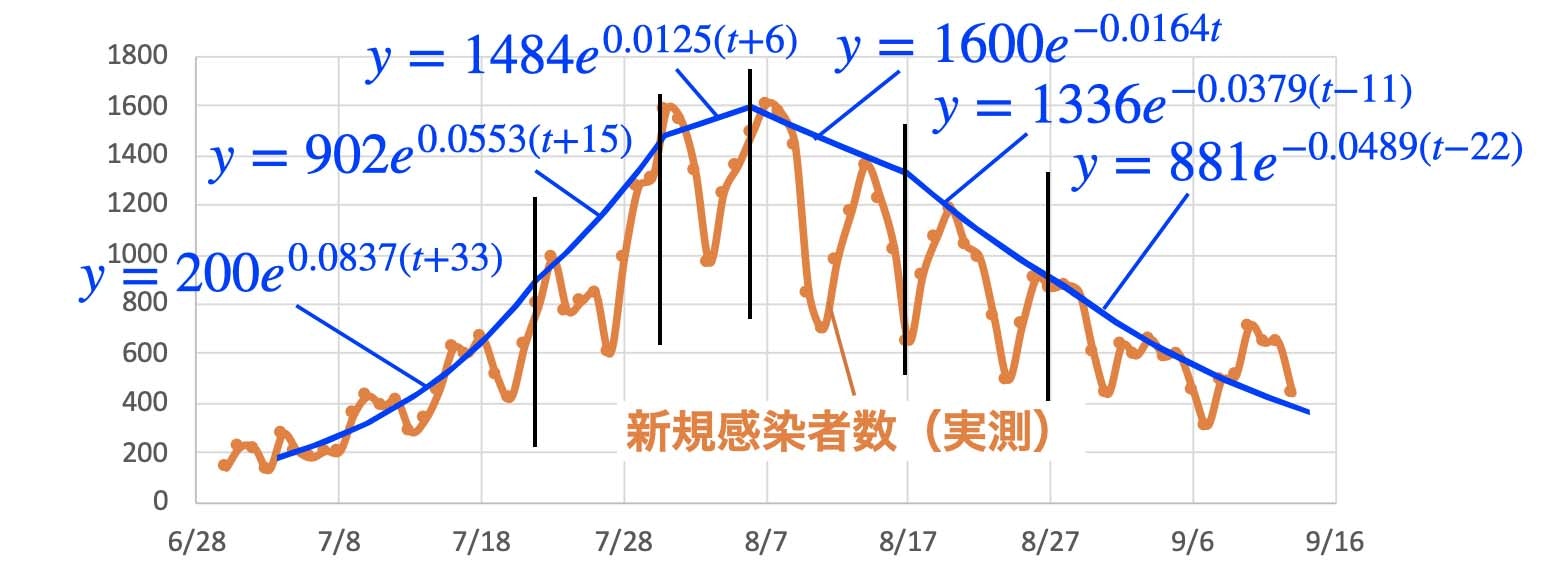
全経過を6つのタイムゾーンに区切って6つの指数係数を使います。時間の経過と共に指数係数が漸減していることがわかります。実効再生産数は指数係数の一次関数であり、平均罹病期間を14日とすると 実効再生産数 = 14 × 指数係数 + 1 で表せます。

タイムゾーン	指数係数	実効再生産数
① 7/3~7/20	0.0837	2.172
② 7/21~7/29	0.0553	1.775
③ 7/30~8/4	0.0125	1.175
④ 8/5~8/15	-0.0164	0.771
⑤ 8/16~8/26	-0.0379	0.470
⑥ 8/27~	-0.0489	0.315

山の始まりの時点から実効再生産数は減り続けています。
指数関数（SIRモデル）で当てはめることによってタイムゾーン毎の実効再生産数の変化がわかります。

新型コロナウイルス街の人出は？全国18地点グラフ | NHK特設サイト ↩