新型コロナウイルス(COVID-19)と SIR モデル
新型コロナウイルス(COVID-19)の患者数推移を表す数理モデル「SIRモデル」をよく目にするようになりました。
SIR モデルでは未感染者をS (susceptible)、感染者を I (infectious)、治癒者や死亡者を R (removed) とします。
S, I, R 各群の増加速度は以下のように表せます。
\begin{align}
\frac{dS}{dt} &= -βSI\\
\frac{dI}{dt} &= βSI-γI\\
\frac{dR}{dt} &= γI\\
\end{align}
$\ β$ は感染率、$\ γ$ は除去率(平均罹病期間の逆数)となります。
\ γ=\frac{1}{平均罹病期間}
$\ 全人口をNとすると基本再生産数\ R_0は$
\ R_0=\frac{βN}{γ}\\
\therefore β=\frac{γR_0}{N}
以上より、2つの係数 $\ γ, β$ は平均罹病期間と基本再生産数 (COVID-19 では2~3)から算出できることが分かります。
上記の微分方程式から、
\begin{align}
\Delta S&=-βSI\Delta t\\
\Delta I&=(βSI-γI)\Delta t\\
\Delta R&=γI\Delta t\\
\ S(t+\Delta t)&=S+\Delta S\\
\ I(t+\Delta t)&=I+\Delta I\\
\ R(t+\Delta t)&=R+\Delta R\\
\end{align}
Excel VBA マクロのコード
上記から Excel VBA マクロのプログラムを作りました。
数学的に微分方程式の解を求めなくても、for ループで各パラメータを漸増させていけば曲線が得られます。
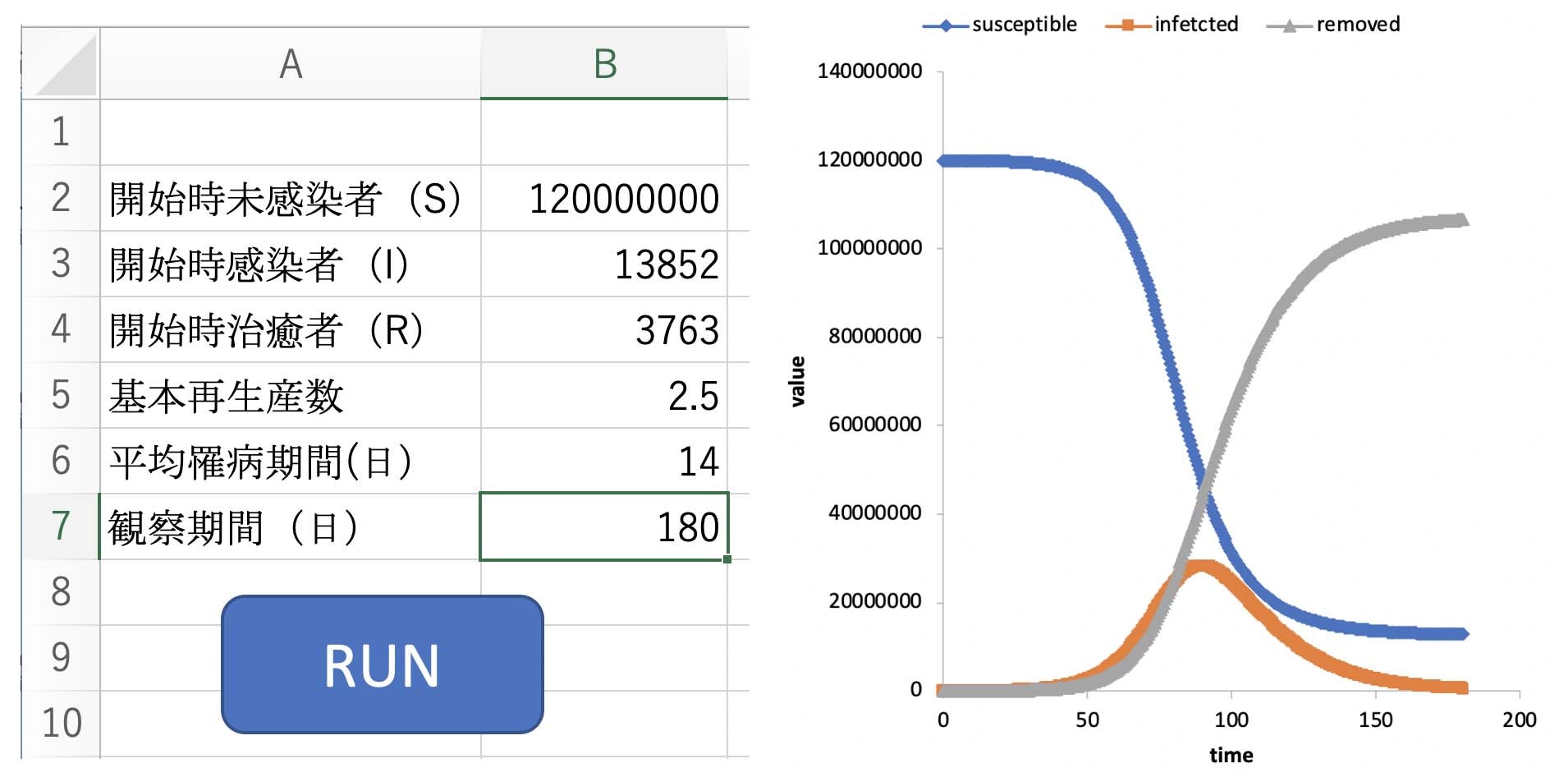
セルB2 を (S) 総人口1億2000万人
セルB3 を (I) 13852人(2020.4.29の患者数)
セルB4 を (R) 3763人(2020.4.29の治癒者+死亡者数)
セルB5 を基本再生産数 2.5
セルB6 を平均罹病期間 14日
セルB7 を観察期間 180日とします。
$\Delta t=0.5日$ とします。
基本再生産数を色々変えてみて下さい。
以下にスクリーンショットとコードを示します。
Sub SIR()
If ActiveSheet.ChartObjects.Count = 1 Then ActiveSheet.ChartObjects(1).Delete
Range(Columns(4), Columns(7)).Clear
S = Range("B2").Value
I = Range("B3").Value
R = Range("B4").Value
saiseisansu = Range("B5").Value
ribyoukikan = Range("B6").Value
kansatsukikan = Range("B7").Value
Dim beta As Double
Dim gam As Double
Dim deltaS As Double
Dim deltaI As Double
Dim deltaR As Double
Dim deltaT As Double
Dim myCount As Integer
gam = 1 / ribyoukikan
beta = saiseisansu * gam / S
deltaT = 0.5
myCount = 0
Cells(1, 4) = "days"
Cells(1, 5) = "susceptible"
Cells(1, 6) = "infetcted"
Cells(1, 7) = "removed"
For myTime = 0 To kansatsukikan Step deltaT
deltaS = -beta * S * I * deltaT
deltaI = (beta * S * I - gam * I) * deltaT
deltaR = gam * I * deltaT
S = S + deltaS
I = I + deltaI
R = R + deltaR
Cells(2 + myCount, 4) = myTime
Cells(2 + myCount, 5) = S
Cells(2 + myCount, 6) = I
Cells(2 + myCount, 7) = R
myCount = myCount + 1
Next myTime
Set trange = Worksheets("Sheet1").Range(Cells(1, 4), Cells(1 + myCount, 7))
Charts.Add
With ActiveChart
.HasLegend = True
.Legend.Position = xlLegendPositionTop
.ChartType = xlXYScatterLines
.SetSourceData Source:=trange, PlotBy:=xlColumns
.Location Where:=xlLocationAsObject, Name:="Sheet1"
End With
With ActiveChart
.Axes(xlValue, xlPrimary).HasTitle = True
.Axes(xlValue, xlPrimary).AxisTitle.Characters.Text = "value"
.Axes(xlValue, xlPrimary).AxisTitle.AutoScaleFont = True
.Axes(xlCategory, xlPrimary).HasTitle = True
.Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time"
.Axes(xlCategory, xlPrimary).AxisTitle.AutoScaleFont = True
.PlotArea.Interior.ColorIndex = 2
.Axes(xlValue).MajorGridlines.Delete
End With
With ActiveSheet
.ChartObjects(1).Top = 50
.ChartObjects(1).Width = 350
.ChartObjects(1).Height = 350
.ChartObjects(1).Left = 600
End With
End Sub
COVID-19 に SIR モデルを当てはめる際の注意点 をご参考ください。