はじめに
感染症の脅威を感じ、数理モデルという言葉を、ニュースでも聞くようになった。僕は、感染症の数理モデルの解析や解析から予想されるアウトカムを研究の対象にしてきた。感染症流行における人為的介入やデータ解析には、僕の力ではとても触れる事ができないが、実装の背景にある数理については、及ばずながら、解説できるのかも知れないと考えた。
数学は、定量化できる現象について、洞察を得ようとする一面を持っていて、ここに、感染症の流行と数学の接点が現れる。感染症の数理は、1927年のKermackとMcKendrickらによる論文を触れずして、語ることは難しい。
彼らが考えた数理モデルは、現代においても中心的な役割を果たしている。彼らが考えた数理モデルの本質を捕まえた基本的なSIRモデルと基本再生産数について説明してみたい。
以下記すことは、目新しいことではなくて、[先駆者たちの様々な文献](# further reading)で何度も解説されている。そちらでより正確で包括的な知識が得られるであろう。これは、基本的な感染症数理モデルであるSIRモデルが、どのように作られるか、基本再生産数の概念がどのように生まれるか、僕なりの言葉で乱雑に焼き直したものである。
SIRモデル:基本的な感染症数理モデル
感染者数の変化率
現実の感染者数が、これから増加するか、または減少に転じるか?このような疑問に答えるには、我々の人口集団において、どのように感染者が生み出されるのか、に目を向ける必要があるだろう。感染症の流行は、感染者が感染者を作り出す、というプロセスによって引き起こされる。
時間$t$における感染者数を$I(t)$で表そう:
$$
I(t)=\text{時間}t{における感染者数}.
$$
この関数がどのように変化するか考えてみたい。感染者数の単位時間あたりの変化率は、関数の微分を使って、$I^\prime(t)$と表される:
$$
I^\prime(t)=\text{感染者数の単位時間あたりの変化率}.
$$
感染者数の変化の要因:新規感染者と感染個体の回復
感染者数の増減を決定する大きな要因は以下の2つである:
- 感染者と未感染者の接触による新規感染による増加
- 感染個体の回復(や死亡)による減少
感染者数の変化を数式で記述したものが感染症の数理モデルである。感染者数の変化率は、パラメータ$\beta$(感染係数)と$\gamma$(回復率)を用いて、
$$
\underbrace{I^\prime(t)}_{感染者数の変化率}=
\underbrace{\beta S(t)I(t)}_{単位時間あたりの新規感染者数}-\underbrace{\gamma I(t)}_{単位時間あたりの回復者数}
\tag{1}$$
と表される。感染者が、新規感染者によって増え、回復者によって減ることを示している。ここで、$S(t)$は、時間$t$における未感染者数を表す(このような個体を感染症に感受性を持つ感受性保持者という)。
未感染者数の変化率は
$$
\underbrace{S^\prime(t)}_{未感染者数の変化率}=-\underbrace{\beta S(t)I(t)}_{単位時間あたりの新規感染者数}
\tag{2}$$
と表される。式(3)は未感染者数が、新規感染によって、減少していくことを表している。
式(1)と(2)で未感染者数と感染者数の変化を記述している。回復者数を$R(t)$として、
$$
R^\prime(t)=\gamma I(t)\tag{3}
$$
の式を付け加えることも多い。この式は、感染症から回復した個体が、回復者となることを表している。(1)(2)(3)式からなる系をSIRモデルと呼ぶ。
このような数理モデルが出来ると何が嬉しいか?一つの利点は、(1)(2)(3)式をコンピュータで、シミュレーションできることである。仮に$\beta,\gamma$のパラメータの値が分かっていれば、それを用いて感染者数の変化について[シミュレーション](# シミュレーション)できる。
基本再生産数-流行初期の感染者数の動態
(1)式を見るまでも無く、新規感染者数を完全に$0$に出来れば、感染症の流行を食い止めることができる。どれくらい接触を食い止めれば、感染症の流行の食い止めが実現できるのか?基本再生産数は、このような疑問に答えるときに重要な概念となる。
流行初期において、人口集団にほぼ感染者がいないことを仮定すれば、全体の人口を$N$として、$S(t)\approx N$と定数で近似出来る。未感染者$S(t)$の変化を無視して、感染症の流行初期における感染者数の変化は次のように表される。
$$
I^\prime(t)=\beta NI(t)-\gamma I(t)
$$
(7)式の$\beta NI(t)$の係数$\beta N$は、単位時間に一人の感染者が作る新規感染者数である。また$1/\gamma$が平均感染期間を表す事が知られている。よって、$\beta N/\gamma$は、「$1$人の感染者が平均感染期間に作り出す新規感染者数」と解釈できる。これを基本再生産数と呼び、$R_0$と表す。基本再生産数が$1$を上回れば、自然と感染症は流行し、逆に$1$を下回れば、感染症の流行は収まっていくだろう。人との接触率を$p\ (0\leq p\leq 1)$だけ下げれば、この指標が
$$
R_e=(1-p)R_0
$$
となり(実効再生産数)、これが$1$を下回るようにすれば良い。実効再生産数については、新型コロナクラスター対策専門家@ClusterJapanでも触れられ、8割の行動制限の必要性が説明されている。
シミュレーション
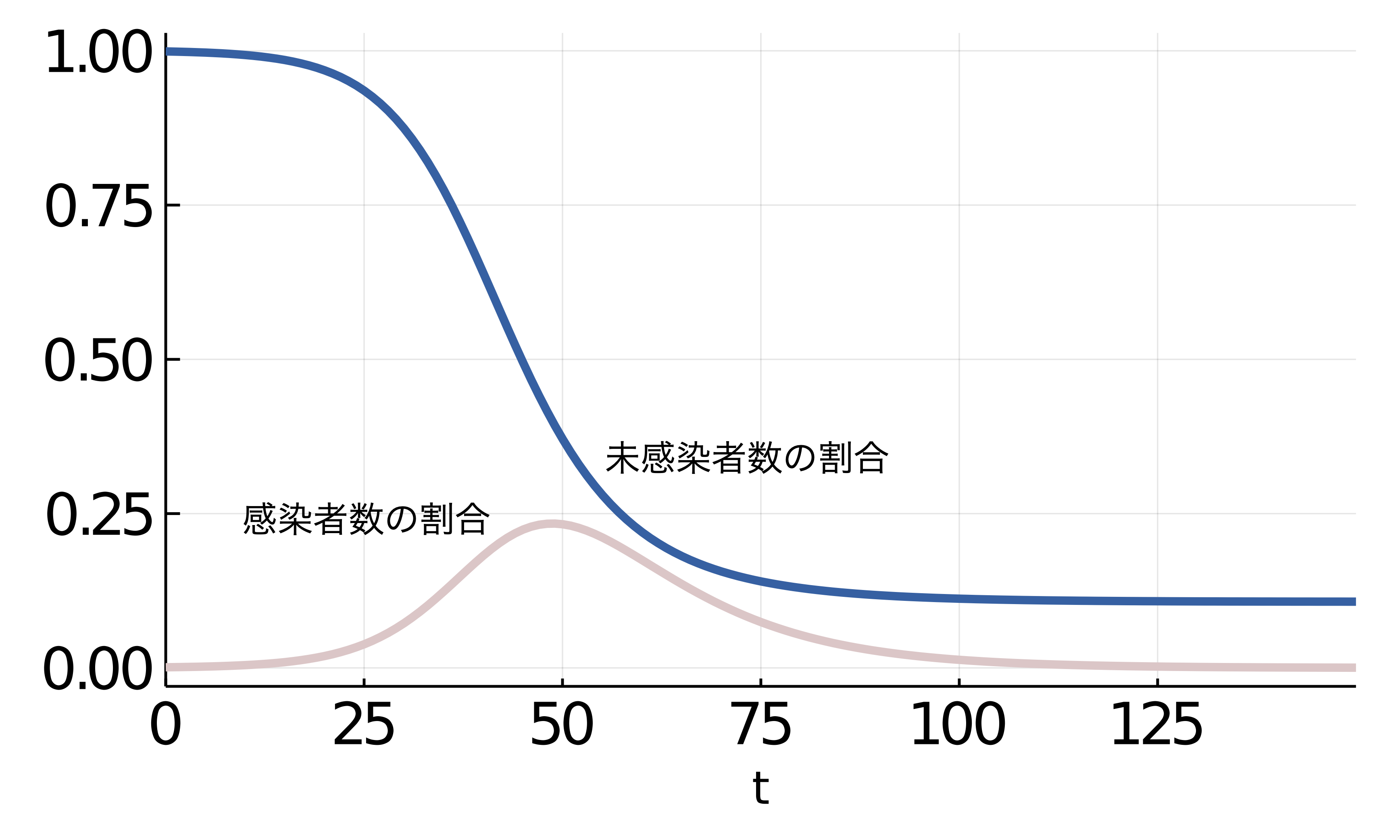
$\gamma=1/10,\beta=2.5\times 1/10$とおいて(怪しい数値だが)、$R_0=2.5$のときのSIRモデルを計算すると、下のようなグラフが得られる。薄紅色の曲線が、感染者数の割合をプロットしたものである。横軸は時間を示している。
上の図から、時間が経てば、感染者数はピークを迎えてから減っていく事がわかる。ただ、そのときの未感染者数の割合に着目して欲しい。感染症が収まる頃には、我々のほとんどが罹患している事が予想される。
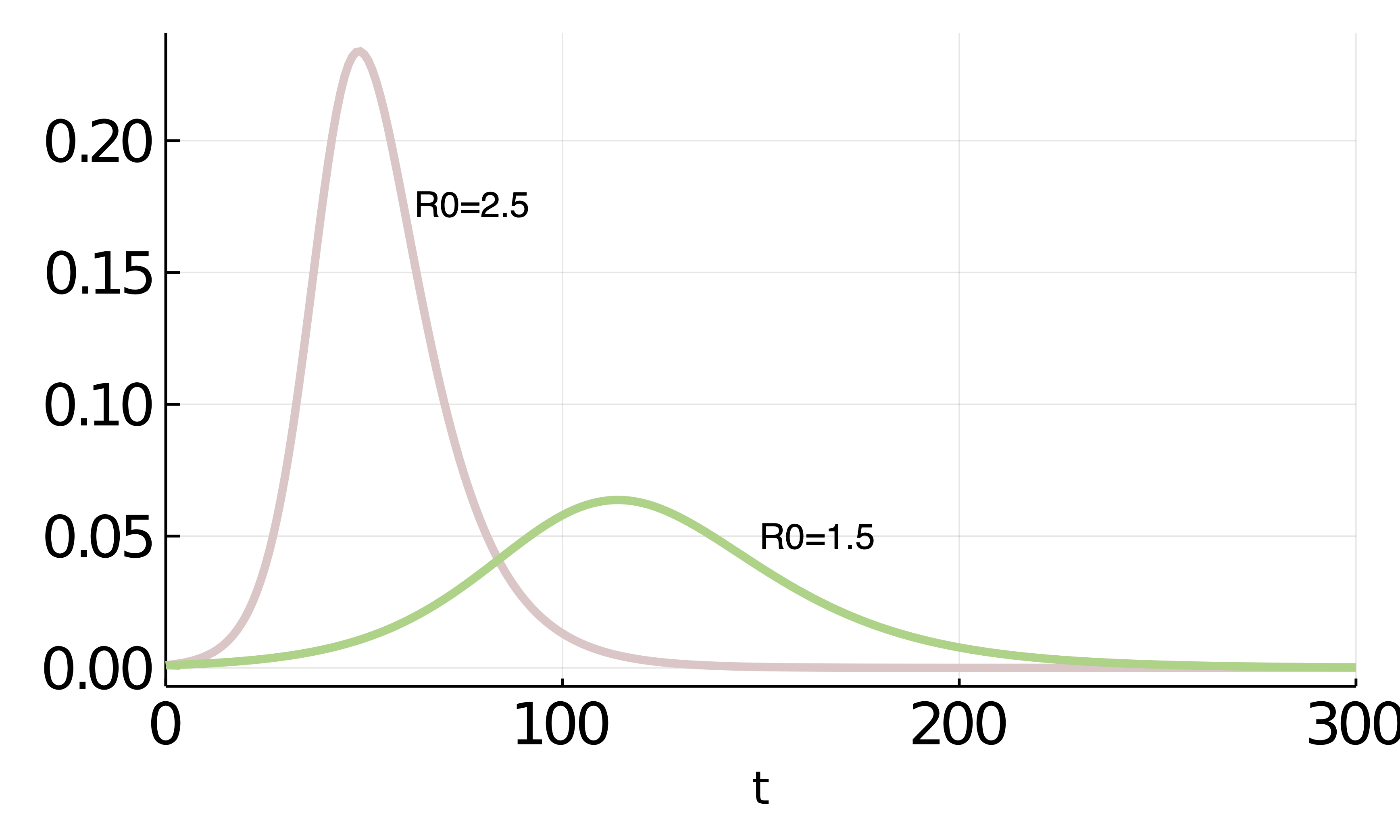
接触率を下げて、$\beta=1.5\times 1/10$とすれば、モデルから異なる流行曲線を得る事ができる。$R_0=2.5$のときと$R_0=1.5$のときの流行曲線を比較したものが下のグラフである。
基本再生産数$R_0$の変化によって、流行曲線の様子が変わることが見てとれる。これが、「患者の増加スピードを抑える」+「流行の規模を下げ、患者数のピークを下げる」対策である(新型コロナウイルスに関するQ&A(一般の方向け)|厚生労働省)。接触率を下げることによって、流行曲線がなだらかになることを目指している。
最後に
SIRモデルはとても単純化されたモデルである。感染者の潜伏期間は無視されているし、感染者の異質性も無視されている。またこのような方程式では、回復期間は指数分布に従う、という仮定がおかれている。死亡する個体を考えていない。空間を移動する個体を考えていない。etcetc.
しかしながら、SIRモデルは、感染者数の増減の要因の本質を記述し、それから感染症の流行動態の描像を描くものとなっている。この数理モデルから学べることは少なくない。
SIRモデルの大きな仮定は、感染症からの回復者がみな免疫を持つ、という点である。この仮定のために、時間が十分経てば、我々は集団免疫を獲得し、感染者数はやがて$0$に収束する。これは果たしてCoronavirus disease 2019 (COVID-19)で 満たされているだろうか。また、型が違うウイルスが集団に入ってきているとすると、このSIRモデルで得られる洞察は、そのまま成り立つだろうか。
数理モデルのブラッシュアップや解析は、現在でも計算機の手が届かない。どのようなモチベーションであれ、感染症の数理に興味を持つ人が増えれば、それが、我々の目前にある現象を理解することにつながるのではないだろうか。
FURTHER READING
SIRモデルの数理的な側面に関しては、以下のテキストに纏まっている。
稲葉寿 「感染症の数理モデル」(2008) 培風館(手に入れるのが困難である。)
稲葉寿, 微分方程式と感染症数理疫学, 数理科学 46(4) (2008) pp. 19-25
数理モデルによる疫学データの扱い方については、西浦博, 稲葉寿, 感染症流行の予測:感染症数理モデルにおける定量的課題, 統計数理 54(2) (2006) 461-480や、稲葉寿 「感染症の数理モデル」(2008) 培風館の2章に書かれている。
他にも、