ゴンペルツ曲線とは何か？（1） #数理モデル

はじめに

Gompertz 曲線（信頼度成長曲線）はプログラムの残存バグ数推測に使われます。
私は職業プログラマではありませんが、数年前にC型肝炎ウイルスと Gompertz 曲線の関係¹について研究していたことがあり Qiita 読者の皆様にも参考になると思い投稿させて頂きます。

指数関数的増加・減少

Gompertz 曲線の解説に入る前に、指数関数的増加・減少について説明します。
高校の数IIIで使った「微分・積分」の教科書を思い出してみましょう。（本稿の内容は高校生レベルです。）
ある一定の倍加時間(a)で分裂して倍増する細胞があるとします。10個の細胞が時間 a 経過すると20個、100個あれば時間 a 経過すると200個になります。10個あった時の単位時間あたりの増加速度は10/a 、100個あった時の単位時間あたりの増加速度は100/a となります。つまり増加速度は、その時に存在する数に比例することになります。
数を N 、増加速度を $\frac{dN}{dt}$ とすると、$\frac{dN}{dt} = kN$ $\ (k$ は比例定数)と表すことができます。
この微分方程式を解きます。

\frac{dN}{dt} = kN\\
\frac{1}{N}dN = kdt\\
\int\frac{1}{N}dN = k\int dt\\
\ln N = kt + c\\
\begin{align}
\ N &= e^{kt + c}\\
&= e^c\ e^{kt}
\end{align}

$\ t = 0$ の時の数を$\ N_0$ とすると、

\ N_0 = e^c

よって

\ N = N_0e^{kt}

上式を対数化すると、

\ln N = \ln {N_0} + kt

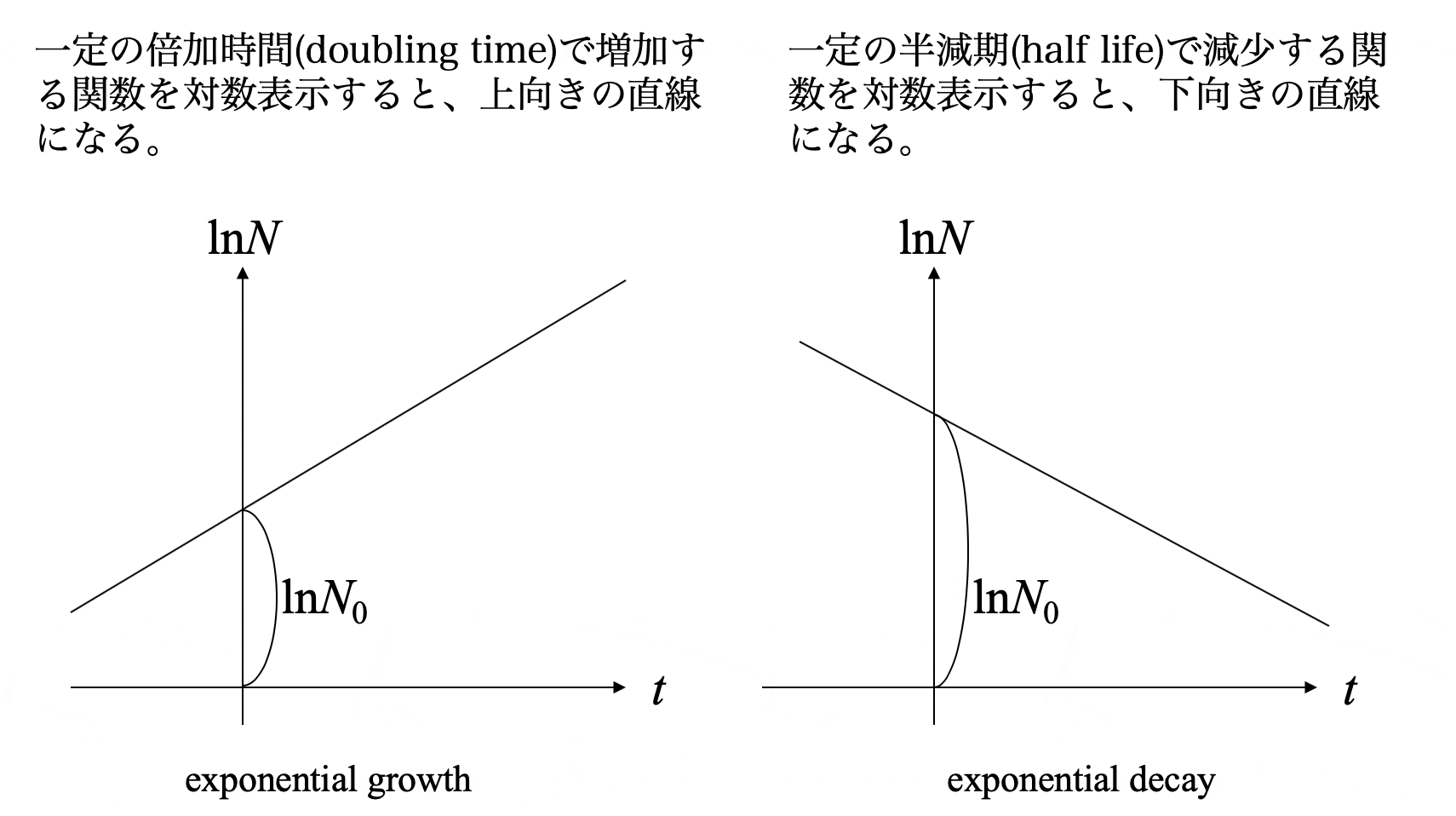
となり、切片を $\ln {N_0}$ 、傾きを $\ k$ とする直線になります。
一方、ある一定の半減期(h)で半減する物の場合は、対数グラフの傾きが $\ -k$ の下向きの直線になります。

Gompertz が見つけたこと

1825年に発表された原著²から解説します。Gompertz はある都市の同一の集団を観察し、10年毎の死亡による人口減少を調べました。

年齢	同一集団の人数	Log (人数)
10	6460	3.81023
20	6090	3.78462
30	5642	3.75143
40	5075	3.70544
50	4397	3.64316
60	3643	3.56146

10歳で6460人いた集団が、10年後（20歳）の時には数名死亡して6090人、30歳では5642人となりました。この変化を対数表示した所、下図のような等比級数的変化を示すことが分かりました。

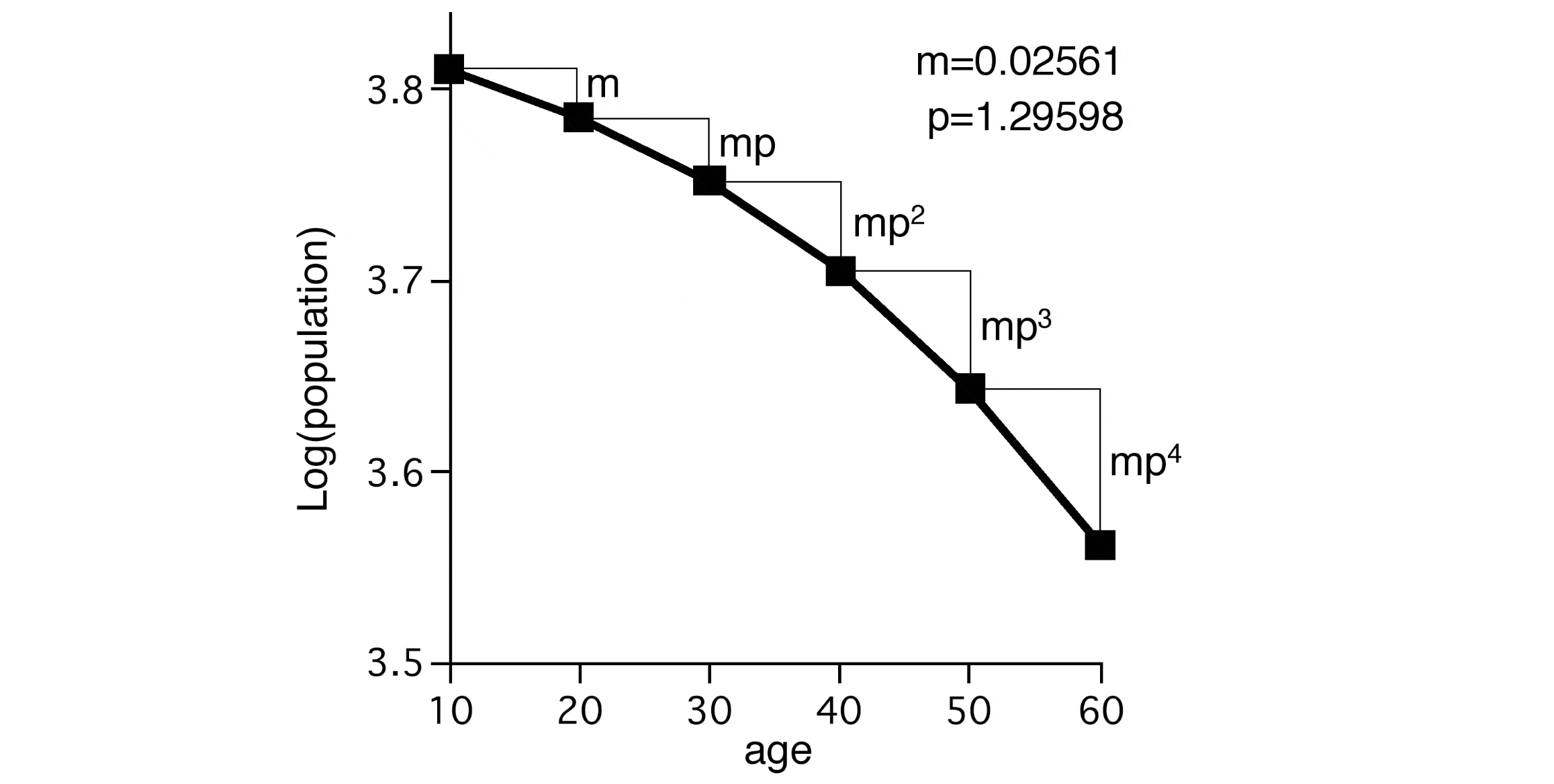
もしこの集団の「死にやすさ」が常に同程度であれば半減期は一定となり、対数グラフにすると下向きの直線になるはずです。ところが、時間の経過と共に傾きが急峻となっています。これは半減期の短縮を意味します。集団が高齢化すればするほど「死にやすさ」が増大して半減期が短縮したのです。

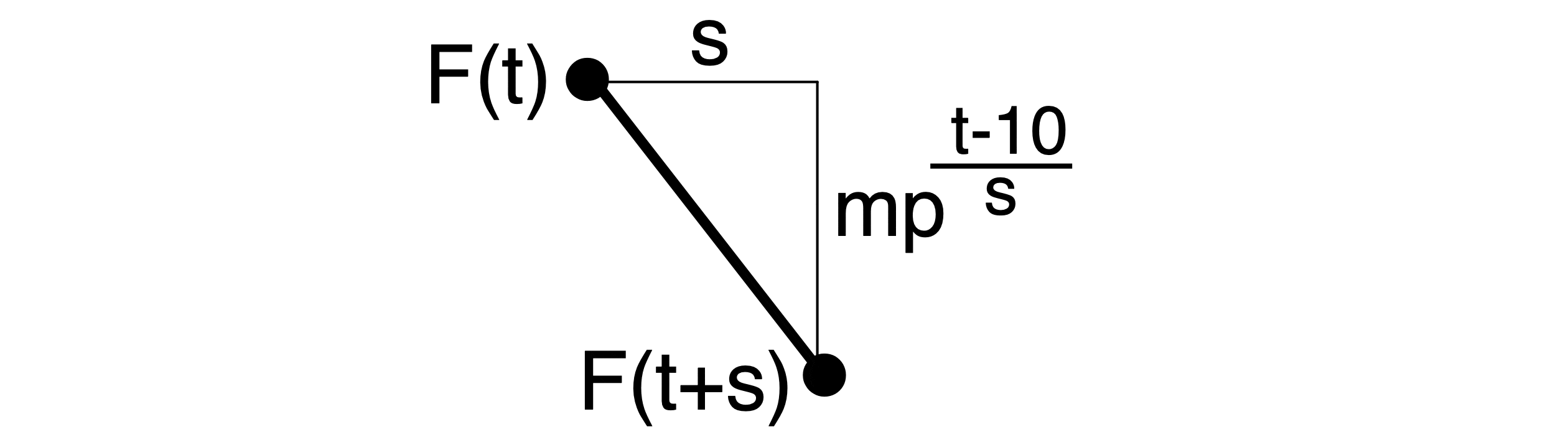
上図で、40歳と50歳のLog(population)の差は $\ mp^3$ となり、$\ F(40)-F(50)=mp^3$ と表せます。
t歳とt+s歳のLog(population)の差は、

\ F(t)-F(t+s)=mp^{\frac{t-10}{s}}

となります。

sが充分に小さい時、関数Fの傾きは

\begin{align}
\frac{dF}{dt} &= \frac{-mp^{\frac{t-10}{s}}}{s}\\
&= -\frac{m}{s}p^{-\frac{10}{s}}p^{\frac{t}{s}}
\end{align}

ここで、

\ -\frac{m}{s}p^{-\frac{10}{s}}=-A_0\hspace{0.5mm},\hspace{1mm}p^{\frac{1}{s}}=e^k

と置き換えることができます。（いずれも定数であるため）
この時、

\frac{dF}{dt}=-A_0e^{kt}

積分すると、

\ F(t)=-\frac{A_0}{k}e^{kt}+c

t = -∞ の時、F(t)は有限の最大値 $\ln{G_{max}}$ となるので、

\ c=\ln{G_{max}}

よって

\ F(t)=\ln{G_{max}}-\frac{A_0}{k}e^{kt}

となります。
以上に示したように、元来 Gompertz 曲線は、人口の経時的な減少を表すために考案されました。Gompertz 理論が生物の増殖曲線に応用出来ることは、Gompertz が原著を発表してから100年後の1926年に発見されました。(Wright, Sewall, book review in Jour. Am. Stat. Assoc., 21, 494, 1926.)
※生物の増殖曲線では $\ e^{kt}$ が $\ e^{-kt}$ に置き換わっています。

まとめ

倍加時間や半減期が一定の時、対数グラフは直線化する。
ゴンペルツ曲線では、加齢による「死にやすさ」の増大が半減期を短縮させる結果、対数グラフが曲線化している。

松井圭司試論「Gompertzian modelを用いたHCV動態の解析」の検証. 肝臓 2009; 50: 324-338. ↩
Gompertz B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos Trans R Soc Lond 1825; 115:513-585. ↩