実測値は Gompertz 曲線に当てはまるか？　その２

累計発生数の検証

ゴンペルツ曲線とは何か？（3）
ゴンペルツ曲線とは何か？（6）
で累計発生数がゴンペルツ曲線に当てはまるかを検証する方法を示しました。
累計発生数を対数化した値を $\ F(t)$ とし、任意の時間間隔を s とします。
対数化された Gompertz 曲線では、以下の式が成り立ちます。

\ F(t+s)=a+bF(t)

$\ F(t+s)$ は切片 a、傾き b の $\ F(t)$ の一次関数となります。

新規発生数の検証

本稿では累計発生数ではなく新規発生数がゴンペルツ曲線に当てはまるかを大まかに推測する方法を示します。
Winsor CP. The Gompertz Curve as a Growth Curve. Proc Natl Acad Sci U S A. 1932;18:1-8.
にゴンペルツ曲線の変曲点に関する記載があり
「累計発生数が最大値の 1/e に達した時が変曲点となる」と述べられています。
（ちなみにロジスティック曲線では最大値の 1/2 に達した時が変曲点になります。）

\ G(t)=81301\times0.0738^{e^{-0.1503(t-8)}}

で表せるゴンペルツ曲線があるとします。
以下に累計発生数 G(t) と1日毎の差分から導いた新規発生数を図示します。

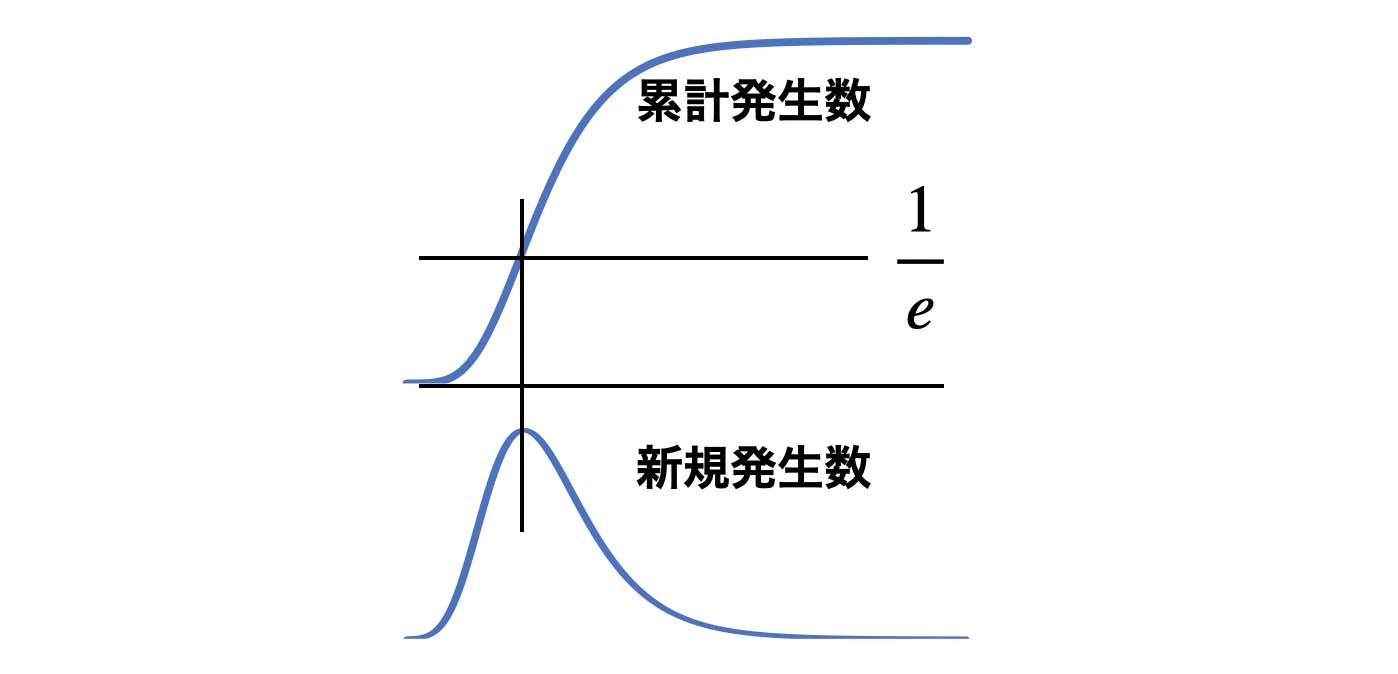
累計発生数が最大値の 1/e に達した時に新規発生数がピークに達していることがわかります。
観測開始からピークまでの発生数 (a) は総数の 1/e = 0.3679
ピークから最大値までの発生数 (b) は総数の 1 – 1/e = 0.6321
a : b = 1 : 1.72 ≒ 1 : √3 となります。
「1 : √3」といえば・・・三角定規の辺の比率ですね。
45°、45°、90°の三角定規の辺の長さは 1 : 1 : √2
30°、60°、90°の三角定規の辺の長さは 1 : 2 : √3

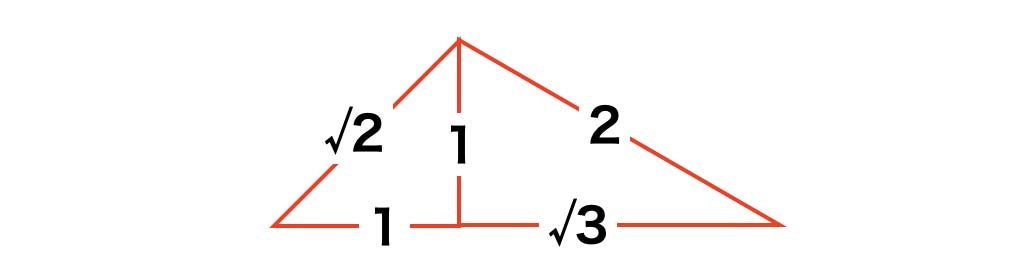
2つの三角定規を上図のように組み合わせると底辺が 1 : √3 に分割できます。

2枚の三角定規の法則

開始からピークまでの発生数：ピークから終焉までの発生数 ≒ 1 : √3 であることを利用して上記の新規発生数を2枚の三角定規に合わせてみましょう。

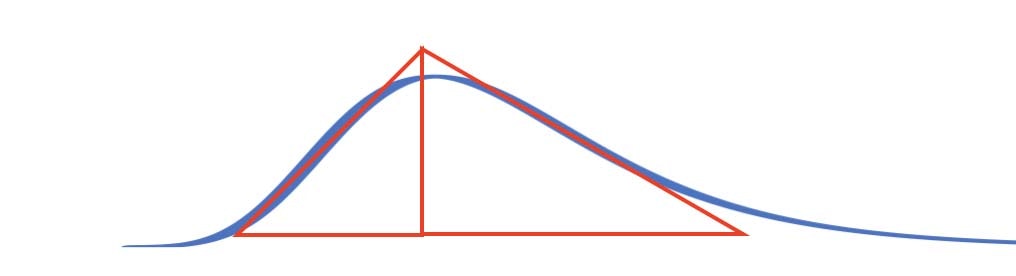
・・・新規発生グラフの縦横比を調整するときれいに2枚の三角定規に fit します。
以下は日本の COVID-19 第1波の新規発生数です。

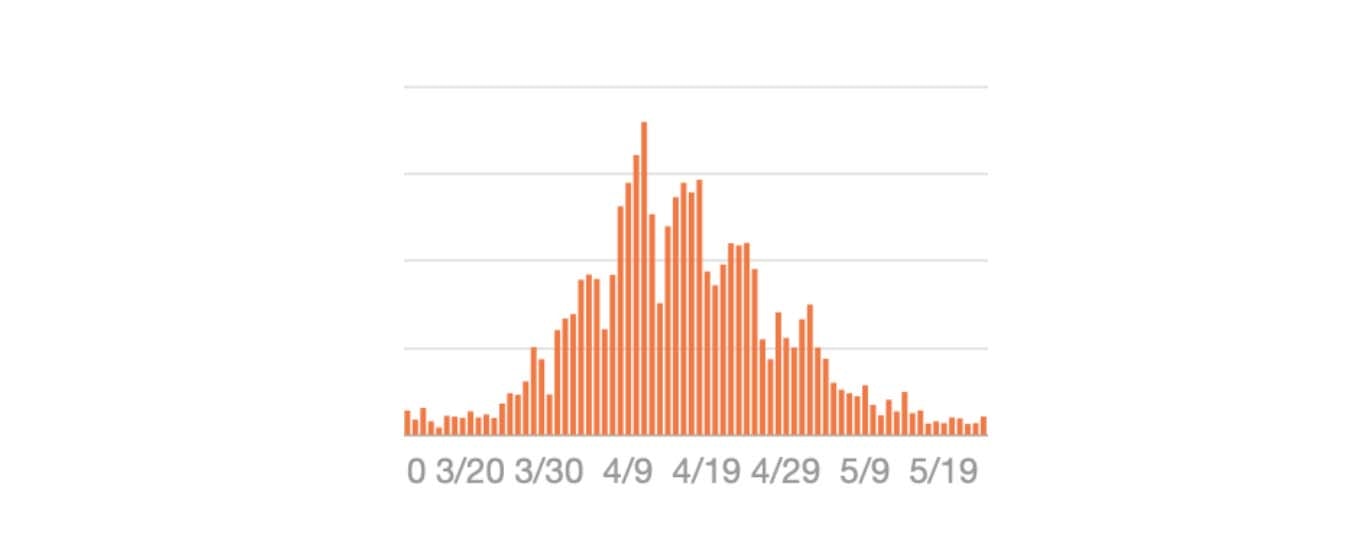
縦横比を調整して2枚の三角定規に当てはめると

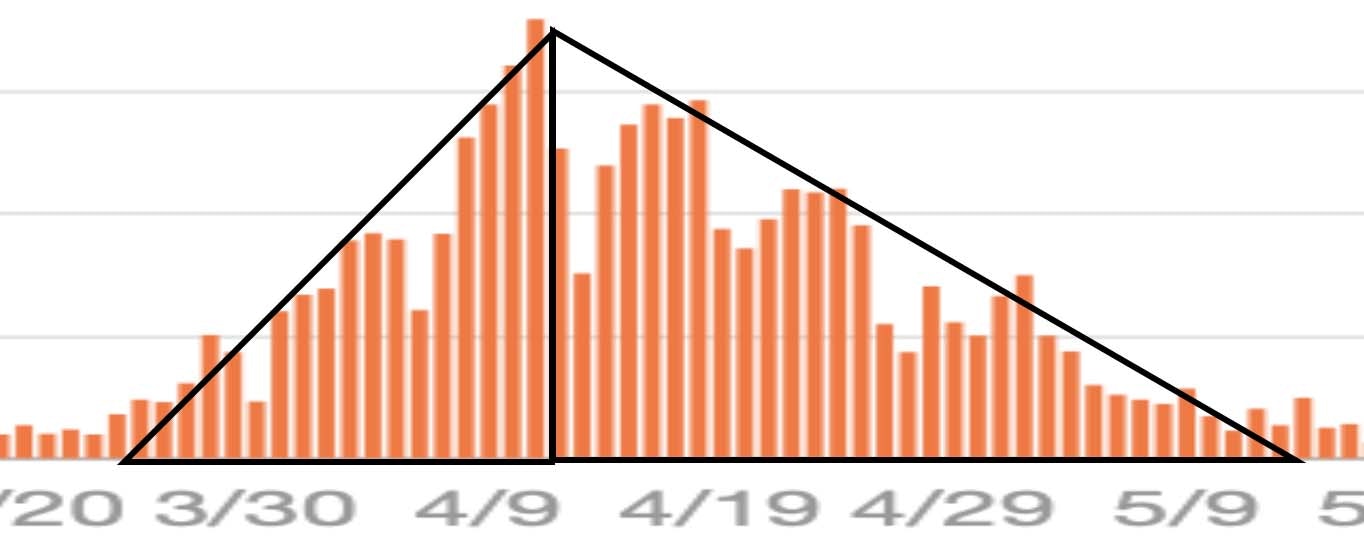
第2波はどうでしょうか

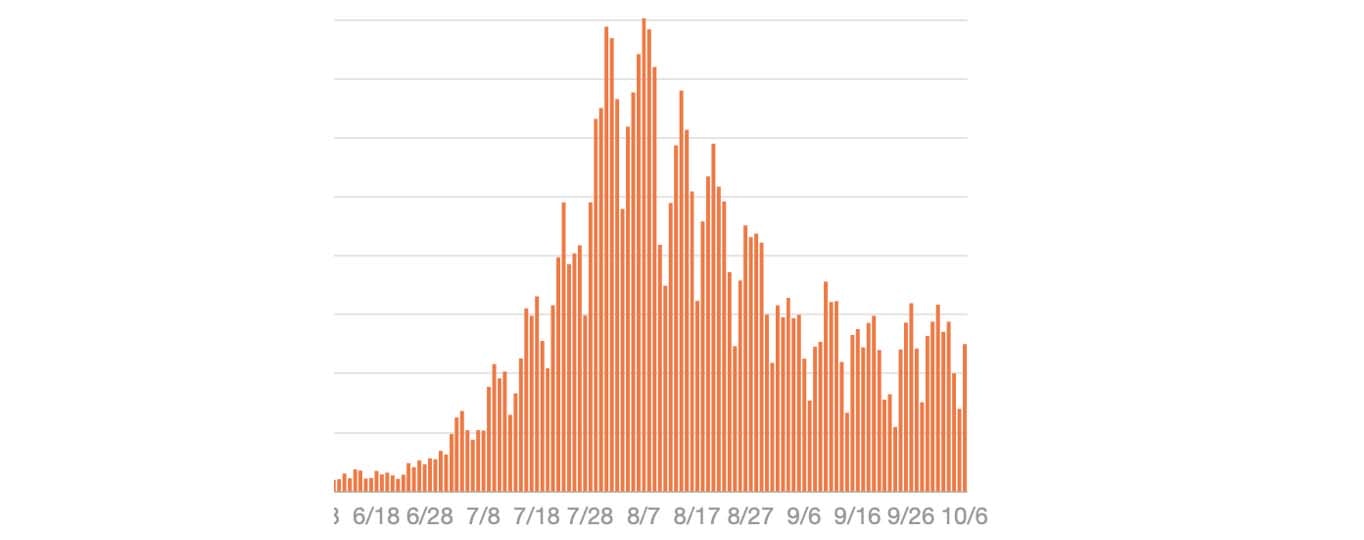
縦横比を調整して2枚の三角定規に当てはめると

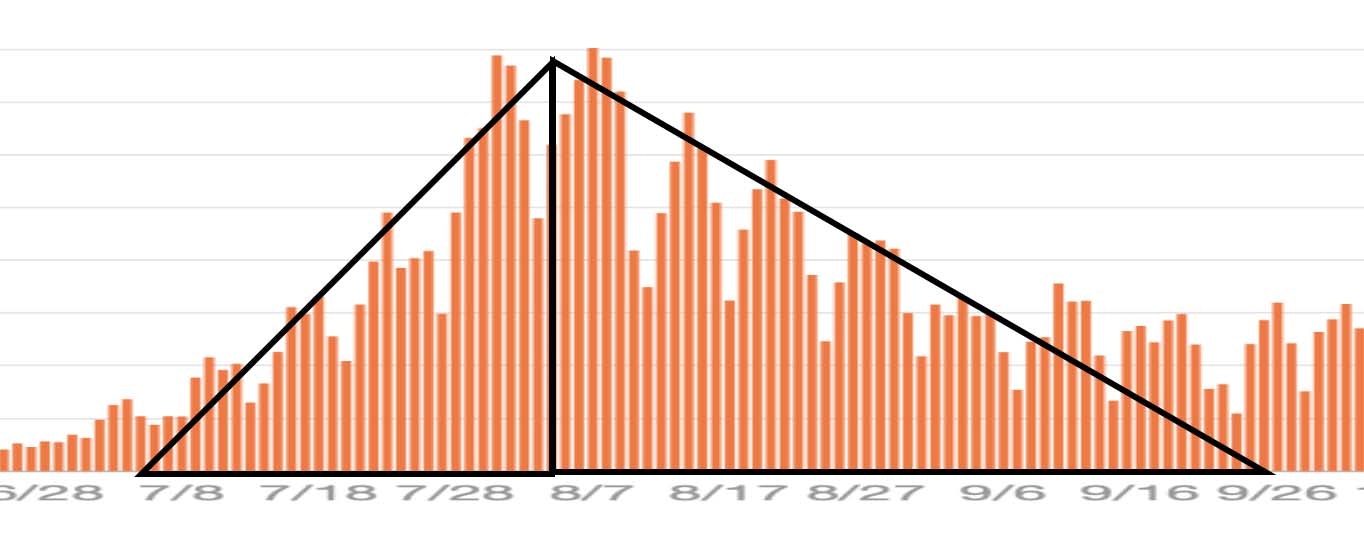
割とよく fit します。
米国の第2波も縦横比を調整すると・・・

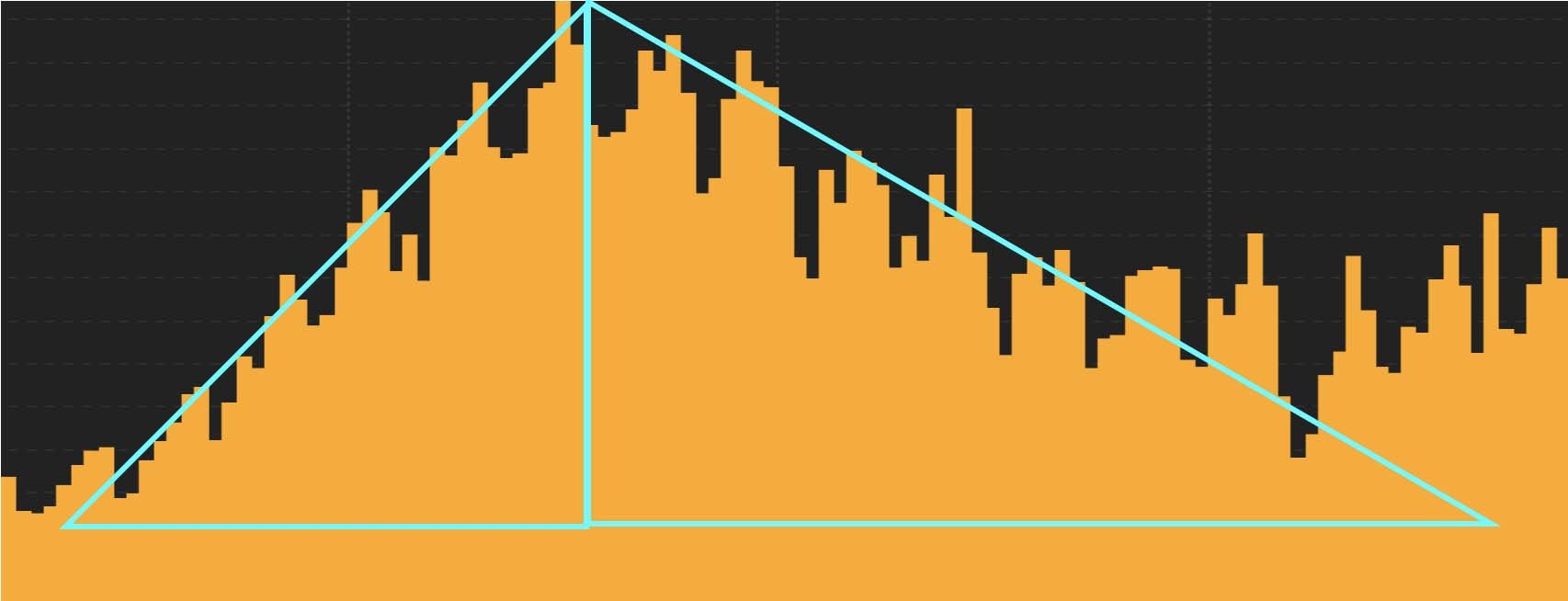
イタリアとドイツの第1波も同様に縦横比を調整すると・・・

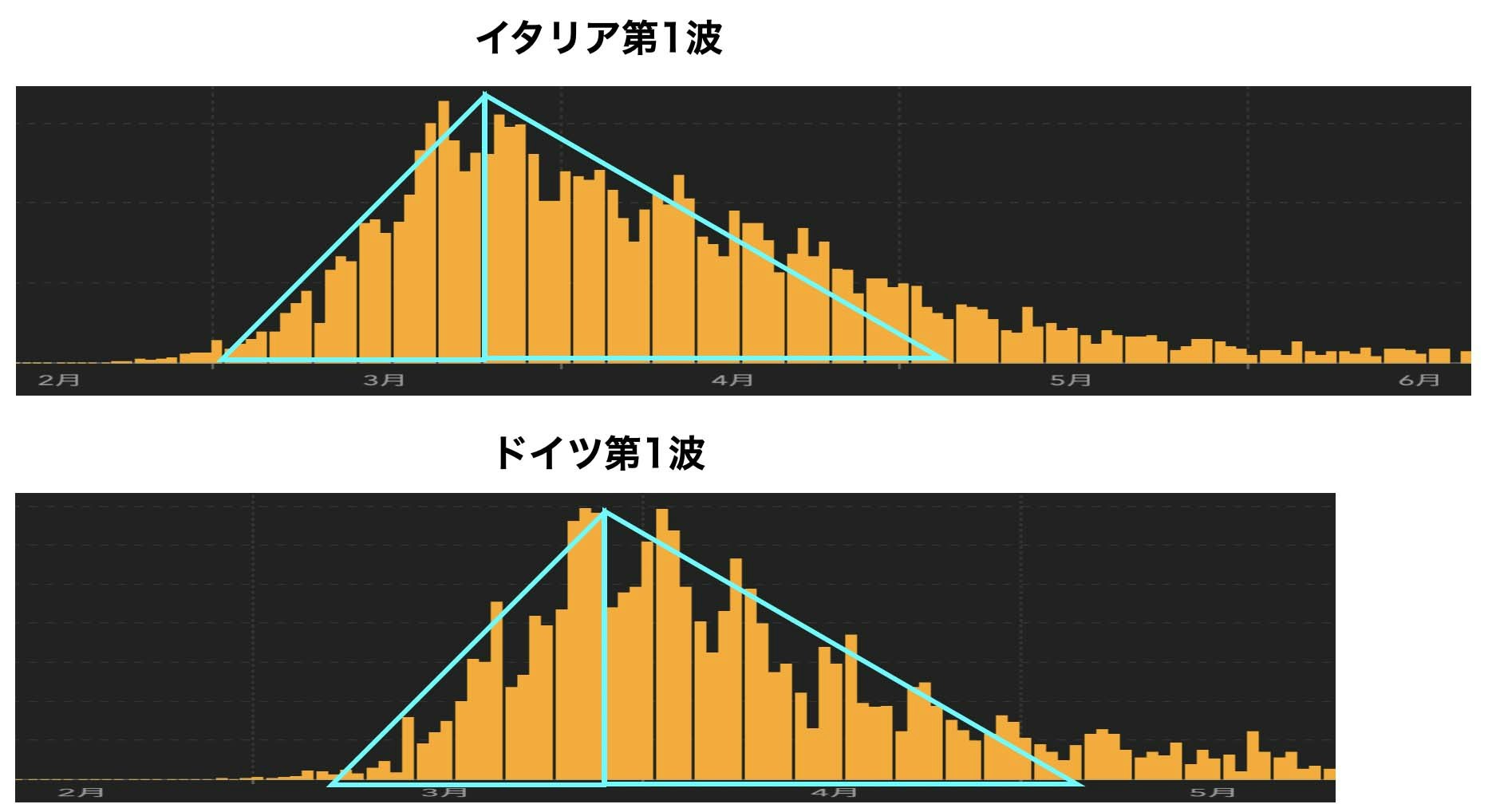
よく fit しています。
※上記はゴンペルツ曲線が当てはまりそうなケースを恣意的に選んでおり、「全ての国の第○波が2枚の三角定規に当てはまる」とは限りませんのでご注意ください。

※追記（2020.12.3）

2020.12.3 時点で日本の第3波に当てはめてみました。

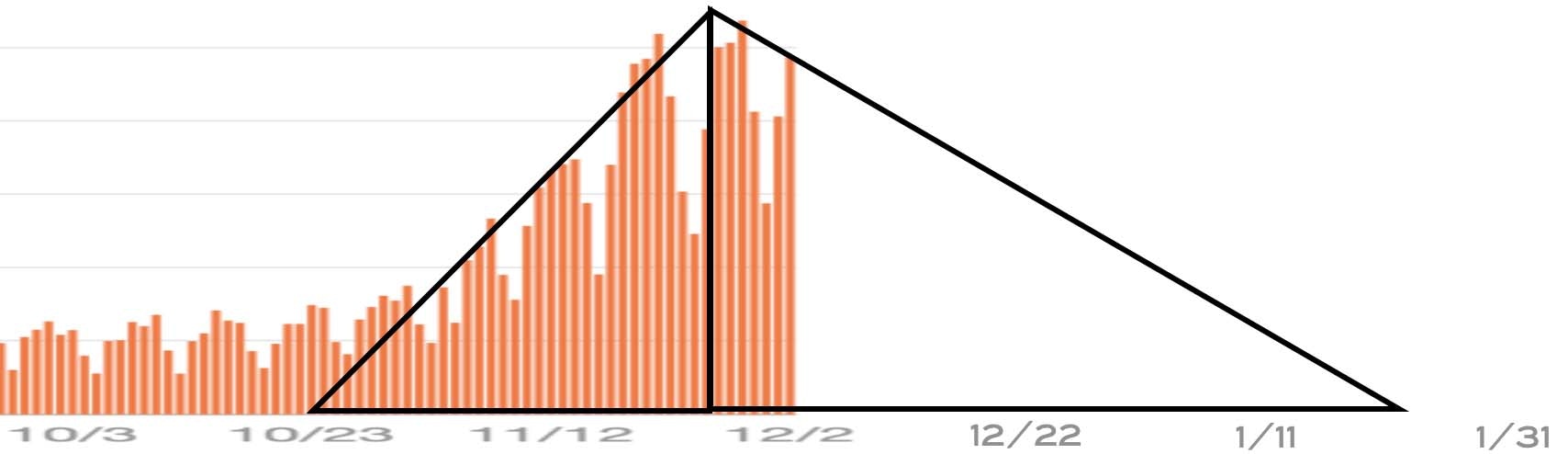
11月の終わりがピークである。
第3波がゴンペルツ曲線に従う。
人々の行動変容の強度が一定である。

と仮定すると第3波の収束は 2021.1.20 頃となる見込みです。
流行開始からピークまでの発生数は総数の 1/e = 0.3679
ピークから収束までの発生数は総数の 1 – 1/e = 0.6321
なので、現時点で病床占有率が37%を超える地域は収束までに病床が満杯になる可能性があります。

※追記（2021.3.8）

Qiita の読者には高校生の方もいらっしゃるので、勉強のために「ゴンペルツ曲線は累計発生数が最大値の 1/e に達した時が変曲点となる」ことを以下に証明します。
累計発生数を

\ G(t)=G_{max}e^{-e^{-kt}}

とします。G_max は最大値、k は減衰係数です。
G(t) を2回微分したもの d²G/dt² が 0 の時、G(t) は変曲点となります。
まずは G(t) を微分してみましょう。

\begin{align}
\ G(t)&=G_{max}e^{-e^{-kt}}\\
\ U=-e^{-kt}&,　V=-kt　とすると\\
\ G(t)&=G_{max}e^U\\
\ U&=-e^V\\
\frac{dG}{dt}&=\frac{dG}{dU}\frac{dU}{dV}\frac{dV}{dt}\\
\frac{dG}{dU}&=G_{max}e^U\\
\frac{dU}{dV}&=-e^V\\
\frac{dV}{dt}&=-k\\
\frac{dG}{dt}&=G_{max}e^U(-e^V)(-k)\\
\ &=kG_{max}e^Ue^V\\
\ &=kG_{max}e^{-e^{-kt}}e^{-kt}\\
\ &=kG(t)e^{-kt}\\
\end{align}\\

dG/dt をもう1回微分します。
(F(t)G(t)) ' = F '(t)G(t) + F(t)G '(t) という公式を使います。

\begin{align}
\frac{dG}{dt}&=kG(t)e^{-kt}\\
\frac{d^2G}{dt^2}&=kG'(t)e^{-kt}+kG(t)(-ke^{-kt})\\
\ &=k^2G(t)e^{-2kt}-k^2G(t)e^{-kt}\\
\ &=k^2G(t)e^{-kt}(e^{-kt}-1)\\
\frac{d^2G}{dt^2}&=0　の時\\
\ e^{-kt}-1&=0\\
\ e^{-kt}&=1\\
\therefore t&=0\\
\ G(0)&=G_{max}e^{-e^0}\\
\ &=G_{max}e^{-1}\\
\ &=\frac{G_{max}}{e}\\
\end{align}\\

ゴンペルツ曲線とは何か？（8）

実測値は Gompertz 曲線に当てはまるか？ その２