前回
筑波大学の機械学習講座：課題のPythonスクリプト部分を作りながらsklearnを勉強する (15)
https://github.com/legacyworld/sklearn-basic

課題 7.3 ロジスティック回帰における勾配法とニュートン法の比較

Youtubeでの解説：第8回(1) 27分あたり
再急降下法の実装が悪いのか、講義で説明している結果を得ることは出来なかった。
リッジ回帰等も入れて試してみたが大きく結果は変わらなかった。

数学的には以下のものを実装している。

再急降下法

E(w) = -\frac{1}{N}\sum_{n=1}^{N}{t_n\,\log\hat t_n + (1-t_n)\,\log(1-\hat t_n)}\\
\frac{\partial E(w)}{\partial w} = X^T(\hat t-t) \\
w \leftarrow w - \eta X^T(\hat t-t)

irisのデータでは$N=150$、$w$は切片を足して5次元
$E(w)$を$N$で割っているのはこうしないとInitial Costが合わないからである。
ただこれでも発散するのは0.1だけで、それ以外はちゃんと収束してしまった。
何か間違っているとは思うがよくわからない。

ニュートン法

\nabla \nabla E(w) = X^TRX\,,R=\hat{t}_n(1-\hat{t}_n)の対角行列 \\
w \leftarrow w-(X^TRX)^{-1}X^T(\hat{t}-t)

ニュートン法は大体あっているが、Final Costは残念ながらかなり違う。
講義の結果ではWeightも3つしか表示されていないのも解せない。

ソースコードはこちら
課題 4.3のソースコードを流用しているのでBaseEstimatorでクラス化しているが、そこに意味は無い。

Homework_7.3.py

# 課題 7.3 ロジスティック回帰における勾配法とニュートン法の比較
# Youtubeでの解説：第8回(1) 27分あたり
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing,metrics
from sklearn.linear_model import LogisticRegression
from sklearn.base import BaseEstimator
import statsmodels.api as sm
from sklearn.datasets import load_iris  
iris = load_iris()

class MyEstimator(BaseEstimator):
    def __init__(self,ep,eta):
        self.ep = ep
        self.eta = eta
        self.loss = []

    def fit(self, X, y,f):
        m = len(y)
        loss = []
        diff = 10**(10)
        ep = self.ep
        # 特徴量の種類
        dim = X.T.shape[1]
        # betaの初期値
        beta = np.zeros(dim).reshape(-1,1)
        eta = self.eta

        while abs(diff) > ep:
            t_hat = self.sigmoid(beta.T,X)
            loss.append(-(1/m)*np.sum(y*np.log(t_hat) + (1-y)*np.log(1-t_hat)))
            # 再急降下法
            if f == "GD":
                beta = beta - eta*np.dot(X,(t_hat-y).reshape(-1,1))
            # ニュートン法
            else:
                # NxNの対角行列
                R = np.diag((t_hat*(1-t_hat))[0])
                # ヘッセ行列
                H = np.dot(np.dot(X,R),X.T)
                beta = beta - np.dot(np.linalg.inv(H),np.dot(X,(t_hat-y).reshape(-1,1)))
            if len(loss) > 1:
                diff = loss[len(loss)-1] - loss[len(loss)-2]
                if diff > 0:
                    break
        self.loss = loss
        self.coef_ = beta
        return self

    def sigmoid(self,w,x):
        return 1/(1+np.exp(-np.dot(w,x)))

# グラフ
fig = plt.figure(figsize=(20,10))
ax = [fig.add_subplot(3,3,i+1) for i in range(9)]

# virginicaかそうでないかだけ考慮する
target = 2
X = iris.data
y = iris.target
# y = 2ではない(virginicaではない)場合は0
y[np.where(np.not_equal(y,target))] = 0
y[np.where(np.equal(y,target))] = 1
scaler = preprocessing.StandardScaler()
X_fit = scaler.fit_transform(X)
X_fit = sm.add_constant(X_fit).T #最初の列に1を加える
epsilon = 10 ** (-8)
# 再急降下法
eta_list = [0.1,0.01,0.008,0.006,0.004,0.003,0.002,0.001,0.0005]
for index,eta in enumerate(eta_list):
    myest = MyEstimator(epsilon,eta)
    myest.fit(X_fit,y,"GD")
    ax[index].plot(myest.loss)
    ax[index].set_title(f"Optimization with Gradient Descent\nStepsize = {eta}\nIterations:{len(myest.loss)}; Initial Cost is:{myest.loss[0]:.3f}; Final Cost is:{myest.loss[-1]:.6f}")
plt.tight_layout()    
plt.savefig(f"7.3GD.png")

# ニュートン法
myest.fit(X_fit,y,"newton")
plt.clf()
plt.plot(myest.loss) 
plt.title(f"Optimization with Newton Method\nInitial Cost is:{myest.loss[0]:.3f}; Final Cost is:{myest.loss[-1]:.6f}")
plt.savefig("7.3Newton.png")

# sklearnのLogisticRegressionによる結果
X_fit = scaler.fit_transform(X)
clf = LogisticRegression(penalty='none')
clf.fit(X_fit,y)
print(f"accuracy_score = {metrics.accuracy_score(clf.predict(X_fit),y)}")
print(f"coef = {clf.coef_} intercept = {clf.intercept_}")

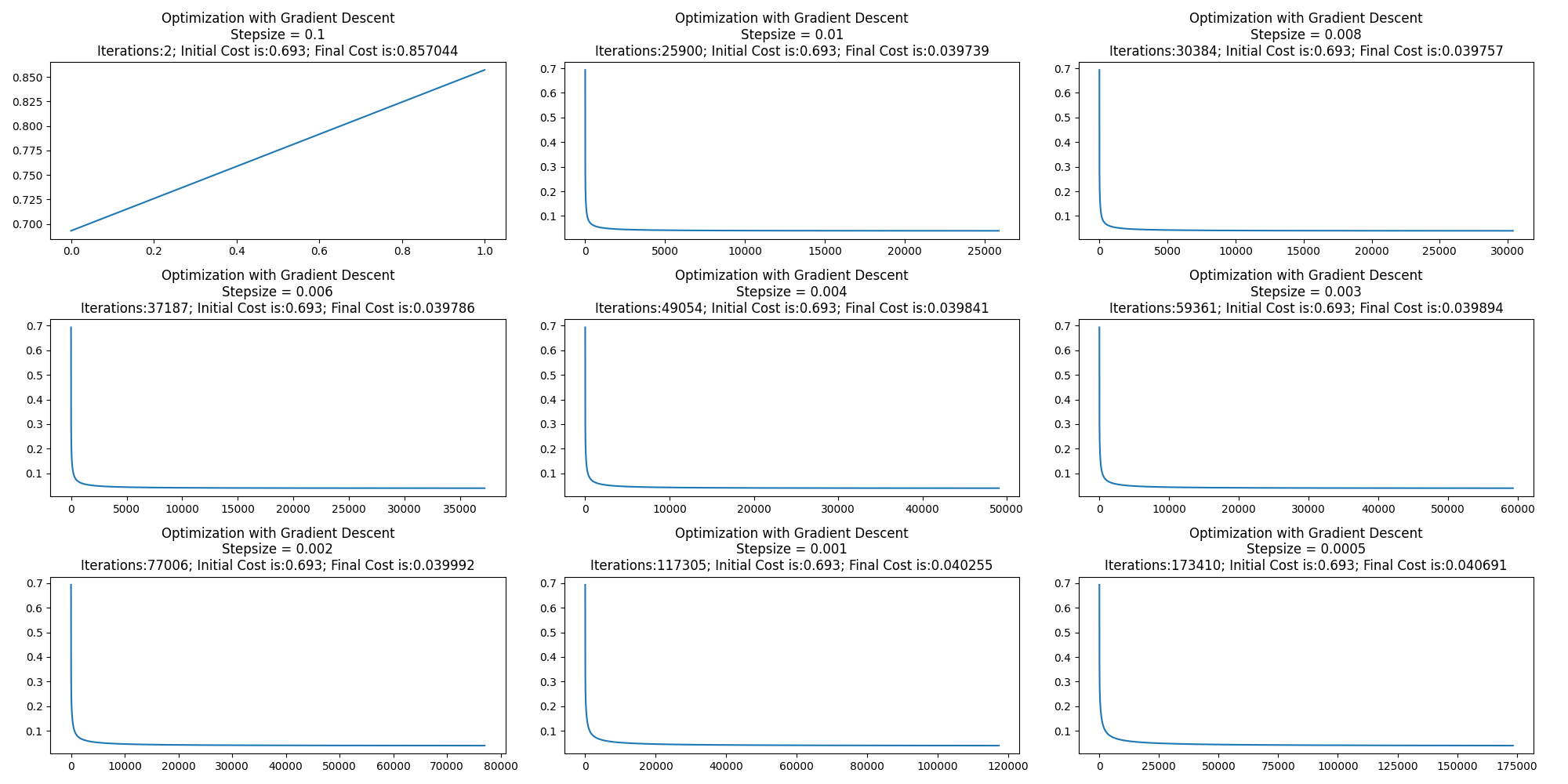
再急降下法の結果

講義ではステップパラメータが0.003までは発散して0.002で最小となるが、全く違う結果となってしまった。

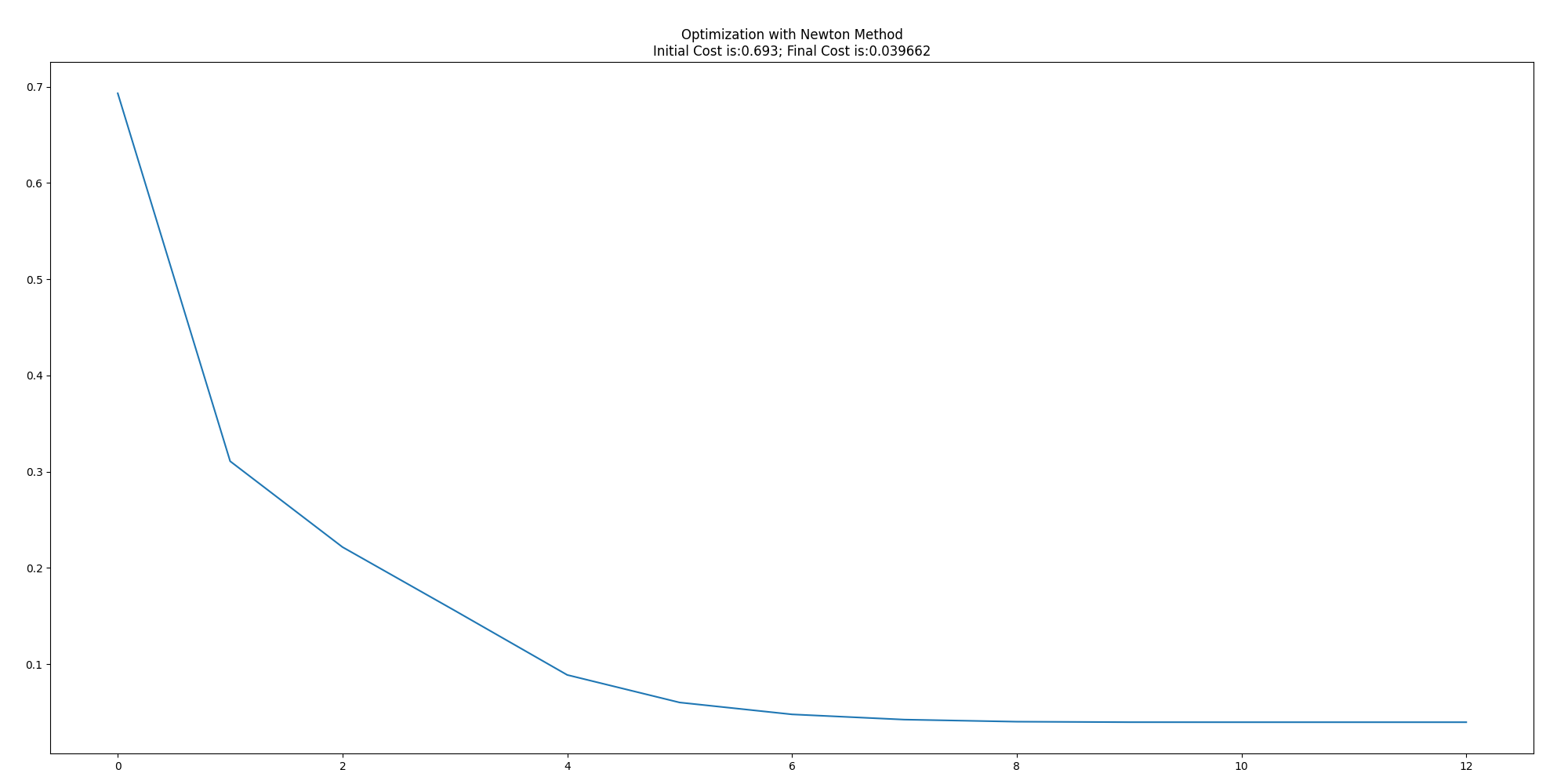
ニュートン法の結果

Final Costは桁が一つ小さいが、回数は講義と大体同じ。そこまで間違ってはいないようだ。

sklearnのLogisticsRegressionの結果

accuracy_score = 0.9866666666666667
coef = [[-2.03446841 -2.90222851 16.58947002 13.89172352]] intercept = [-20.10133936]

結果

得られたパラメータ以下の通り
再急降下法はFinal Costの一番小さかったステップサイズ=0.01の時の結果

再急降下法:(w_0,w_1,w_2,w_3,w_4) = (-18.73438888,-1.97839772,-2.69938233,15.54339092,12.96694841)\\
ニュートン法:(w_0,w_1,w_2,w_3,w_4) = (-20.1018028,-2.03454941,-2.90225059,16.59009858,13.89184339)\\
sklearn:(w_0,w_1,w_2,w_3,w_4) = (-20.10133936,-2.03446841,-2.90222851,16.58947002,13.89172352)

ニュートン法は確かに速いのだが逆行列計算が必須なので、次元数とかサンプル数が増えると結局は確率的再急降下法に落ち着くのであろうか？

過去の投稿

筑波大学の機械学習講座：課題のPythonスクリプト部分を作りながらsklearnを勉強する (16)