前回
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (5)
https://github.com/legacyworld/sklearn-basic
課題 4.2 リッジ回帰とラッソの正則化パス
Youtubeでの解説:第5回(1) 15分50秒あたり
課題 4.1とほぼ同じだが、今度は正則化パラメータをより大きく振って($10^{-3} ~ 10^{6}$)、各係数への影響を見ていく問題となっている。
リッジとラッソの違いがはっきりと判るので良い課題だと思う。
ソースコードはこれ。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn import preprocessing
# scikit-leanよりワインのデータをインポートする
df= pd.read_csv('winequality-red.csv',sep=';')
# 目標値であるqualityが入っているので落としたdataframeを作る
df1 = df.drop(columns='quality')
y = df['quality'].values.reshape(-1,1)
scaler = preprocessing.StandardScaler()
# 正則化パラメータ
alpha = 10 ** (-4)
X = df1.values
X_fit = scaler.fit_transform(X)
# 結果格納用のDataFrame
df_ridge = pd.DataFrame(columns=np.append(df1.columns,'alpha'))
df_lasso = pd.DataFrame(columns=np.append(df1.columns,'alpha'))
while alpha <= 10 ** 6 + 1:
# リッジ回帰
model_ridge = linear_model.Ridge(alpha=alpha)
model_ridge.fit(X_fit,y)
tmp_se = pd.Series(np.append(model_ridge.coef_[0],alpha),index=df_ridge.columns)
df_ridge = df_ridge.append(tmp_se,ignore_index=True)
# ラッソ回帰
model_lasso = linear_model.Lasso(alpha=alpha)
model_lasso.fit(X_fit,y)
tmp_se = pd.Series(np.append(model_lasso.coef_,alpha),index=df_lasso.columns)
df_lasso = df_lasso.append(tmp_se,ignore_index=True)
alpha = alpha * 10 ** (0.1)
for column in df_ridge.drop(columns = 'alpha'):
plt.plot(df_ridge['alpha'],df_ridge[column])
plt.xscale('log')
plt.gca().invert_xaxis()
plt.savefig("ridge.png")
plt.clf()
for column in df_lasso.drop(columns = 'alpha'):
plt.plot(df_lasso['alpha'],df_lasso[column])
plt.xscale('log')
plt.gca().invert_xaxis()
plt.savefig("lasso.png")
因みにwhile alpha <= 10 ** 6 + 1:の+1は、これがないと最後の$10^{6}$が実行されないからである。
alpha = alpha * 10 ** (0.1)と刻んでいるのが原因だろうと思う。
今回は描画にあたって2つ変更している。
X軸のみを対数にする(方対数)にするplt.xscale('log')とX軸を逆にする(右側が小さい)plt.gca().invert_xaxis()
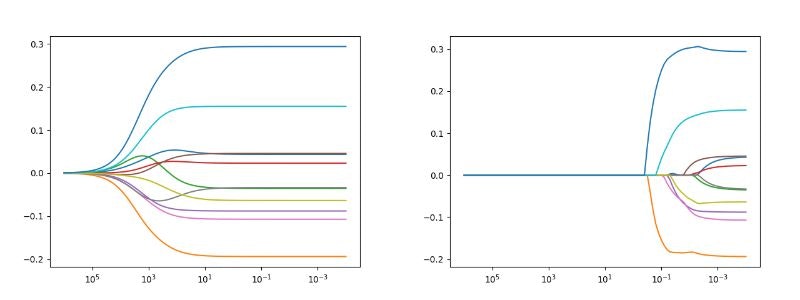
全体的に徐々に正則化が効いてくるリッジと係数の小さいものから0に収束するラッソの違いが鮮明に出ている。
(問題は$10^{-3}$からだったが解説のリッジ回帰が$10^{-2}$から描画されていたので変更している)
リッジとラッソ共に、正則化パラメータが大きくなっている途中で係数の絶対値が大きくなるパターンが見える。
以下のグラフはその動きをする特徴量だけを抜き出して描画したものである。
リッジの方が大きく動いて見えるが、Y軸のスケールが10倍違うだけである。
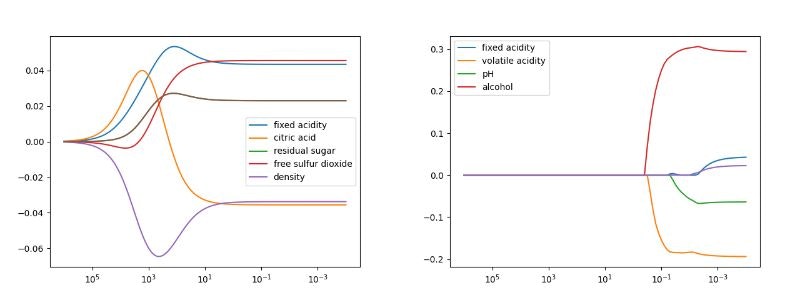
とある特徴量の係数が小さくなるとそれまで目立たなかったものが表面化してくる、という動きなんだろうけどよくわからない。
このような動きがあるとは思わなかったので機械学習は一筋縄ではいかないと思わせる良い課題でした。
過去の投稿
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (1)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (2)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (3)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (4)