筑波大学の機械学習講座：課題のPythonスクリプト部分を作りながらsklearnを勉強する (1)
筑波大学の機械学習講座：課題のPythonスクリプト部分を作りながらsklearnを勉強する (2)
筑波大学の機械学習講座：課題のPythonスクリプト部分を作りながらsklearnを勉強する (3)
https://github.com/legacyworld/sklearn-basic
課題 3.4 多項式単回帰の正則化
さて、今回はリッジ回帰である。
Youtubeの解説はないようにみえるが、一部結果が第4回(1) 9分45秒あたりにある。
ソースコードとしては課題 3.2とほぼほぼ同じである。
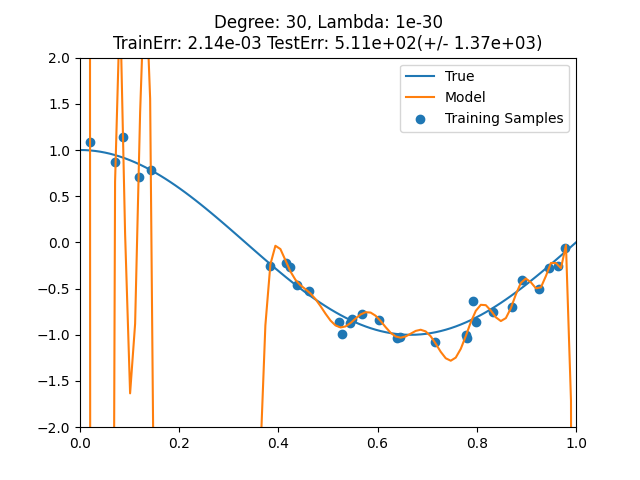
今回の課題では次数は30に固定している。
その代わりに正則化パラメータを[1e-30,1e-20,1e-10,1e-5, 1e-3,1e-2,1e-1, 1,10,100]で動かしていく。
ソースコード内では正則化パラメータはalphaとしている。Pythonのlambdaは予約されているので。
Homework_3.4.py
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures as PF
from sklearn import linear_model
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
DEGREE = 30
def true_f(x):
return np.cos(1.5 * x * np.pi)
np.random.seed(0)
n_samples = 30
# 描画用のx軸データ
x_plot = np.linspace(0,1,100)
# 訓練データ
x_tr = np.sort(np.random.rand(n_samples))
y_tr = true_f(x_tr) + np.random.randn(n_samples) * 0.1
# Matrixへ変換
X_tr = x_tr.reshape(-1,1)
X_plot = x_plot.reshape(-1,1)
degree = DEGREE
alpha_list = [1e-30,1e-20,1e-10,1e-5, 1e-3,1e-2,1e-1, 1,10,100]
for alpha in alpha_list:
plt.scatter(x_tr,y_tr,label="Training Samples")
plt.plot(x_plot,true_f(x_plot),label="True")
plt.xlim(0,1)
plt.ylim(-2,2)
filename = f"{alpha}.png"
pf = PF(degree=degree,include_bias=False)
linear_reg = linear_model.Ridge(alpha=alpha)
steps = [("Polynomial_Features",pf),("Linear_Regression",linear_reg)]
pipeline = Pipeline(steps=steps)
pipeline.fit(X_tr,y_tr)
plt.plot(x_plot,pipeline.predict(X_plot),label="Model")
y_predict = pipeline.predict(X_tr)
mse = mean_squared_error(y_tr,y_predict)
scores = cross_val_score(pipeline,X_tr,y_tr,scoring="neg_mean_squared_error",cv=10)
plt.title(f"Degree: {degree}, Lambda: {alpha}\nTrainErr: {mse:.2e} TestErr: {-scores.mean():.2e}(+/- {scores.std():.2e})")
plt.legend()
plt.savefig(filename)
plt.clf()
print(f"正則化パラメータ = {alpha}, 訓練誤差 = {mse}, テスト誤差 = {-scores.mean():.2e}")
変更しているのは
linear_reg = linear_model.Ridge(alpha=alpha)
だけである。
このプログラムを実行すると以下のようなWarningが出る。
/usr/local/lib64/python3.6/site-packages/sklearn/linear_model/_ridge.py:190: UserWarning: Singular matrix in solving dual problem. Using least-squares solution instead.
warnings.warn("Singular matrix in solving dual problem. Using "
これはコレスキー分解というところで出ているようなのだがよくわからなかった。
linear_model/ridge.py
try:
# Note: we must use overwrite_a=False in order to be able to
# use the fall-back solution below in case a LinAlgError
# is raised
dual_coef = linalg.solve(K, y, sym_pos=True,overwrite_a=False)
except np.linalg.LinAlgError:
warnings.warn("Singular matrix in solving dual problem. Using "
"least-squares solution instead.")
dual_coef = linalg.lstsq(K, y)[0]
連立方程式が解けないから最小二乗法でやるよ、ということのようだが・・・
1e-30,1e-20だけで出る理由は何なのかわからなかった。
実行結果
正則化パラメータ = 1e-30, 訓練誤差 = 0.002139325105436034, テスト誤差 = 5.11e+02
正則化パラメータ = 1e-20, 訓練誤差 = 0.004936191193133389, テスト誤差 = 5.11e+02
正則化パラメータ = 1e-10, 訓練誤差 = 0.009762751388489265, テスト誤差 = 1.44e+02
正則化パラメータ = 1e-05, 訓練誤差 = 0.01059565315043209, テスト誤差 = 2.79e-01
正則化パラメータ = 0.001, 訓練誤差 = 0.010856091742299396, テスト誤差 = 6.89e-02
正則化パラメータ = 0.01, 訓練誤差 = 0.012046102850453813, テスト誤差 = 7.79e-02
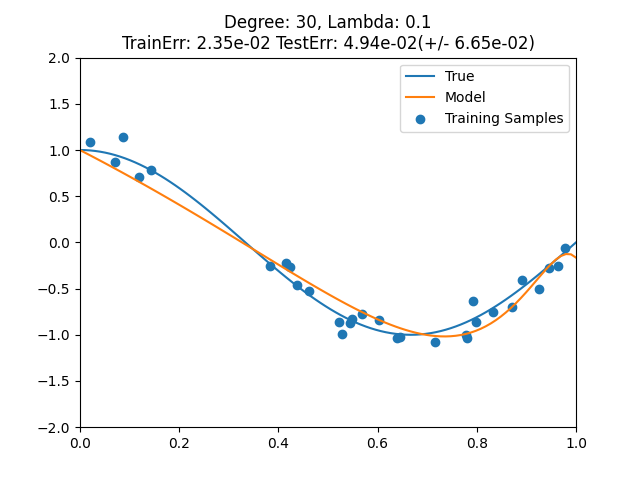
正則化パラメータ = 0.1, 訓練誤差 = 0.02351033489834412, テスト誤差 = 4.94e-02
正則化パラメータ = 1, 訓練誤差 = 0.11886509938269865, テスト誤差 = 2.26e-01
正則化パラメータ = 10, 訓練誤差 = 0.31077333649742883, テスト誤差 = 4.71e-01
正則化パラメータ = 100, 訓練誤差 = 0.41104732329314453, テスト誤差 = 5.20e-01
-
最も小さい訓練誤差
- 正則化パラメータ = 1e-30
-
最も小さいテスト誤差
- 正則化パラメータ = 0.1
- 解説では0.01が一番良いとのことだがこのプログラムでは0.1の方がテスト誤差が小さかった
正則化が効きすぎると平均を取るだけになるし、効きが弱いと過学習になってしまう。
なのでリッジ回帰でも正則化パラメータのチューニングに交差検証は必要。