前回
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (6)
https://github.com/legacyworld/sklearn-basic
課題 4.3 最急降下法と確率的最急降下法
解説は第5回(1) 21分あたり
課題を読んだときは楽勝と思ったのだが、解説を見てみるとscikit-learnそのままでは無理だった(多分)
理由としてはステップで動いていく毎にLossを表示するグラフを書く方法が見当たらなかったからである。
せっかくなのでいろいろ勉強するために下記を実装した。
- 自作の再急降下法
- 自作の再急降下法を使って交差検証をする
ググると再急降下法自体はいくらでもあるのだが、リッジ回帰を入れたものがあまり見当たらない。
数学的な説明は一応これだろう。
https://www.kaggle.com/residentmario/ridge-regression-cost-function
\lambda = 正則化パラメータ,
\beta = \begin{pmatrix} \beta_0 \\ \beta_1\\ \vdots \\ \beta_m \end{pmatrix},
y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{pmatrix},
X = \begin{pmatrix}
1&x_{11}&x_{12}&\cdots&x_{1m}\\
1&x_{21}&x_{22}&\cdots&x_{2m}\\
\vdots\\
1&x_{N1}&x_{N2}&\cdots&x_{Nm}
\end{pmatrix}\\ \\
\beta^{t+1} = \beta^{t}(1-2\lambda\eta) - \eta\frac{1}{N}X^T(X\beta^t-y) (※2020/5/31訂正)
今回のワインデータだと$m = 11,N=1599$
プログラムに当てはめると
$\lambda$ : l
$\beta$ : beta
$\eta$ : eta
X : X_fit (MyEstimatorの中ではX)
y : y
プログラムは下記を参照させていただいた。
初歩からの機械学習:最急降下法による重回帰モデル~PythonとRでスクラッチから~
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn.base import BaseEstimator
from sklearn.model_selection import cross_validate
import statsmodels.api as sm
class MyEstimator(BaseEstimator):
def __init__(self,ep,eta,l):
self.ep = ep
self.eta = eta
self.l = l
self.loss = []
# fit()を実装
def fit(self, X, y):
self.coef_ = self.grad_desc(X,y)
# fit は self を返す
return self
# predict()を実装
def predict(self, X):
return np.dot(X, self.coef_)
def grad_desc(self,X,y):
m = len(y)
loss = []
diff = 10**(10)
ep = self.ep
# 特徴量の種類
dim = X.shape[1]
# betaの初期値
beta = np.ones(dim).reshape(-1,1)
eta = self.eta
l = self.l
while abs(diff) > ep:
loss.append((1/(2*m))*np.sum(np.square(np.dot(X,beta)-y)))
beta = beta*(1-2*l*eta) - eta*(1/m)*np.dot(X.T,(np.dot(X,beta)-y))
if len(loss) > 1:
diff = loss[len(loss)-1] - loss[len(loss)-2]
self.loss = loss
return beta
# scikit-leanよりワインのデータをインポートする
df= pd.read_csv('winequality-red.csv',sep=';')
# 目標値であるqualityが入っているので落としたdataframeを作る
df1 = df.drop(columns='quality')
y = df['quality'].values.reshape(-1,1)
X = df1.values
scaler = preprocessing.StandardScaler()
X_fit = scaler.fit_transform(X)
X_fit = sm.add_constant(X_fit) #最初の列に1を加える
epsilon = 10 ** (-7)
eta_list = [0.3,0.1,0.03]
loss = []
coef = []
for eta in eta_list:
l = 10**(-5)
test_min = 10**(9)
while l <= 1/(2*eta):
myest = MyEstimator(epsilon,eta,l)
myest.fit(X_fit,y)
scores = cross_validate(myest,X_fit,y,scoring="neg_mean_squared_error",cv=10)
if abs(scores['test_score'].mean()) < test_min:
test_min = abs(scores['test_score'].mean())
loss = myest.loss
l_min = l
coef = myest.coef_
l = l * 10**(0.5)
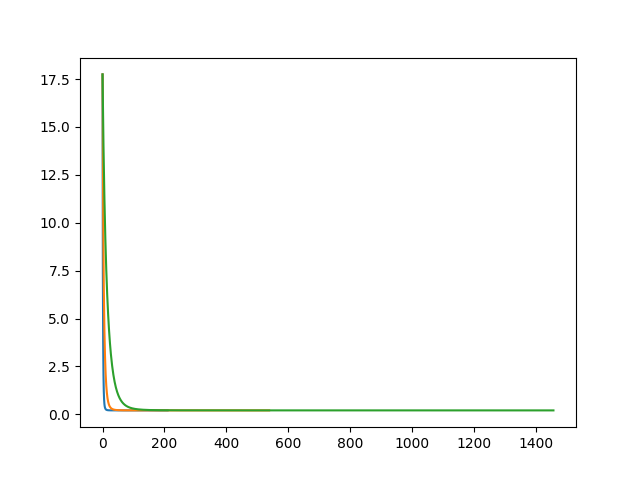
plt.plot(loss)
print(f"eta = {eta} : iter = {len(loss)}, loss = {loss[-1]}, lambda = {l_min}")
# 係数の出力 一番最初に切片が入っているので2つ目から取り出して、最後に切片を出力
i = 1
for column in df1.columns:
print(column,coef[i][0])
i+=1
print('intercept',coef[0][0])
plt.savefig("gd.png")
交差検証も入れてみたのでEstimatorを自作している。
Estimatorは要するにlinear_model.Ridgeみたいなもので、cross_validationの引数に入れるといい具合にK-fold等をやってもらえる。
クラス(名前は何でもよい)に最低2つのメソッド(fit,predict)を実装すればよい。非常に簡単である。
計算も単純で、$\beta$を変えていきながらcostを計算して、costが$\epsilon$(epsilon)より小さくなれば終了である。
この計算途中のloss.appendの部分でステップを変えた際にどのように変化するかをリストに格納している。
今回は解説動画で全くソースコードが見えないため、正則化パラメータを何に設定しているかわからなかった。
sklearnのSGDregressorでのデフォルト値(=0.0001)だとは思うが、これも交差検証のテスト誤差が最小になるところを探ってみた。
なので、ループが2重になっている。
$\eta$を0.3,0.1,0.03で変えながら、$\lambda$を$10^{-5}$から$\frac{1}{2\eta}$まで変化させている。
$1-2\lambda\eta$がマイナスにならないところまでにしている。
計算終了の判定をする$\epsilon$は計算回数が解説と同じになるぐらいにすると$10^{-7}$であった。
大体形は一緒なので良しとする。
実際に求められた係数と切片もほぼ正しい。
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (1)
上記のリンク先で求めたものとそこまで変わりはない。
eta = 0.3 : iter = 211, loss = 0.20839282208794876, lambda = 0.000316227766016838
fixed acidity 0.049506870332573755
volatile acidity -0.19376515874038097
citric acid -0.03590899184362026
residual sugar 0.02477115609195419
chlorides -0.08766609020245213
free sulfur dioxide 0.04504300145052993
total sulfur dioxide -0.1066524471717945
density -0.039236958974544434
pH -0.060484490718680374
sulphates 0.1558562351611723
alcohol 0.29101267115037016
intercept 5.632460233437699
eta = 0.1 : iter = 539, loss = 0.20839849335391505, lambda = 0.000316227766016838
fixed acidity 0.05411085995631372
volatile acidity -0.19374570028895227
citric acid -0.03641567617051897
residual sugar 0.026096674744724647
chlorides -0.08728538562384357
free sulfur dioxide 0.044674324756584935
total sulfur dioxide -0.10616011146688299
density -0.04332301301614413
pH -0.05803157075853309
sulphates 0.15635770126837817
alcohol 0.28874633335328637
intercept 5.632460233437699
eta = 0.03 : iter = 1457, loss = 0.2084181454096448, lambda = 0.000316227766016838
fixed acidity 0.06298223685986547
volatile acidity -0.19369711526783526
citric acid -0.03737402225868385
residual sugar 0.028655773905239445
chlorides -0.08655776298773829
free sulfur dioxide 0.04397075187169952
total sulfur dioxide -0.10522175105302445
density -0.051210328173935296
pH -0.05330134909461606
sulphates 0.15732818468260018
alcohol 0.28436648926510527
intercept 5.632460233437668
過去の投稿
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (1)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (2)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (3)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (4)
筑波大学の機械学習講座:課題のPythonスクリプト部分を作りながらsklearnを勉強する (5)
https://github.com/legacyworld/sklearn-basic