はじめに
私はこれまで機械学習のパラメータチューニングに関し、様々な書籍やサイトで学習を進めてきました。
しかしどれもテクニックの解説が主体のものが多く、
「なぜチューニングが必要なのか?」
という目的に関する記載が非常に少なかったため、体系的な理解に苦労しました。
この経験を後世に役立てられるよう、**「初心者でも体系的に理解できる丁寧さ!」**をモットーに記事にまとめたいと思います。
具体的には、
1. パラメータチューニングの目的
2. チューニングの手順とアルゴリズム一覧
3. Pythonでの実装手順 (SVMでの分類を例に)
の手順で解説を進めます。
独自解釈も含まれるため、間違っている点等ございましたら指摘頂けると有難いです。
なお、文中のコードは**こちらのGitHubにもアップロードしております。**
2021/9/6追記:LightGBMのチューニング実行例追加
以下の記事に、LightGBMでのパラメータチューニング実行例を追加しました
1. パラメータチューニングの目的
1-1. パラメータチューニングの適用対象
1-2. 背景 ~機械学習の複雑化~
1-3. ハイパーパラメータとは何か?
1-4. チューニングの目的
について解説します。
本章は長いので、「早く実践に移りたい!」という方は、1-4まで飛んでいただければと思います
1-1. パラメータチューニングの適用対象
今回紹介するパラメータチューニングは、主に教師あり学習(回帰+分類)を対象とした手法となります
(例)
回帰:気温、湿度、曜日からアイスクリームの売り上げ**(目的変数=数値)を予測する
分類:長さ、重さ、色から果物の種類(目的変数=クラス)**を推定する
詳細は後述しますが、
パラメータチューニングの目的を端的に言うと、回帰・分類において
「複雑な推定」を「未知のデータでも推定性能が上がるよう調整」
することとなります。
##1-2. 背景 ~機械学習の複雑化~
まずは回帰を例に解説します
回帰の中で最も単純な手法が、下図のような「線形回帰」です
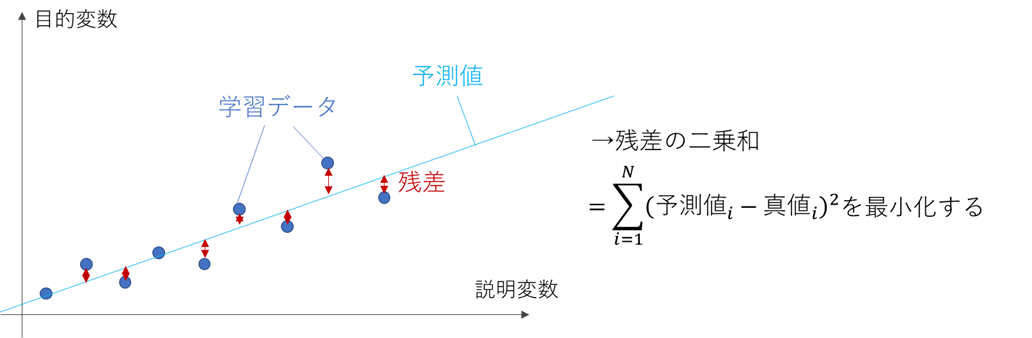
例えば気象庁のサイトから下記のようなデータをダウンロードし、
※気温、気圧は1月の平均を使用
city,altitude,latitude,temperature,pressure
Asahikawa,119.8,43.75666667,-7.5,995.3
Sapporo,17.4,43.06,-3.6,1009.8
Morioka,155.2,39.69833333,-1.9,996.1
Sendai,38.9,38.26166667,1.6,1010.2
Nagano,418.2,36.66166667,-0.6,966.6
Matsumoto,610,36.24666667,-0.4,943.5
Karuizawa,999.1,36.34166667,-3.5,897.6
Kawaguchiko,859.6,35.5,-0.6,913.7
Fujisan,3775.1,35.36,-18.4,626.5
Tokyo,25.2,35.69166667,5.2,1011.4
Nagoya,51.1,35.16666667,4.5,1011.6
Takayama,560,36.155,-1.4,950.9
Osaka,23,34.68166667,6,1009.5
Fukuoka,2.5,33.58166667,6.6,1020.1
Kagoshima,3.9,31.555,8.5,1017.3
Amami,2.8,28.37833333,14.8,1019.6
Naha,28.1,26.20666667,17,1014.5
説明変数=標高(altitude)、目的変数=圧力(pressure)としてscikit-learnで線形回帰すると(参考)
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
df_temp = pd.read_csv(f'./sample_data/temp_pressure.csv')
lr = LinearRegression() # 線形回帰用クラス
X = df_temp[['altitude']].values # 説明変数(標高)
y = df_temp[['pressure']].values # 目的変数(気圧)
lr.fit(X, y) # 線形回帰実施
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('altitude [m]') # x軸のラベル
plt.ylabel('pressure [hPa]') # y軸のラベル
plt.text(1000, 700, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
下図のようになります。
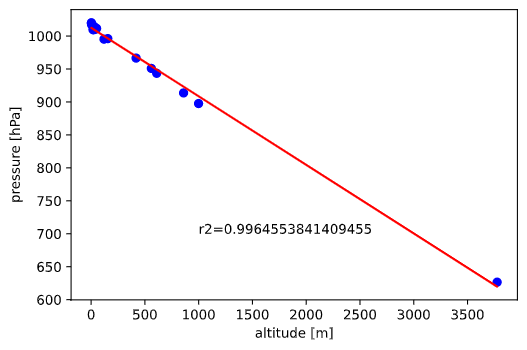
直線で綺麗に回帰できることが分かります(R2=0.996)
が!しかし、実際の現象はもっと複雑で、様々な工夫を凝らさないとうまく予測できない事が多いです。
これら**「複雑な現象に対応する工夫」**として、下記3種類の手法がよく使われます。
A. 多次元の説明変数
B. 非線形
C. 汎化性能の向上(正則化)
もちろん、これ以外の工夫もありますが、今回は代表例としてこの3つを紹介します。
A. 多次元の説明変数
例えば上の気象庁データで、
説明変数=標高(altitude)、目的変数=気温(temperature)とするとどうなるでしょうか?
X = df_temp[['altitude']].values # 説明変数(標高)
y = df_temp[['temperature']].values # 目的変数(気温)
lr.fit(X, y)
plt.scatter(X, y, color = 'blue')
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('altitude [m]')
plt.ylabel('temperature [°C]')
plt.text(1000, 0, f'r2={r2_score(y, lr.predict(X))}') # R2乗値を表示
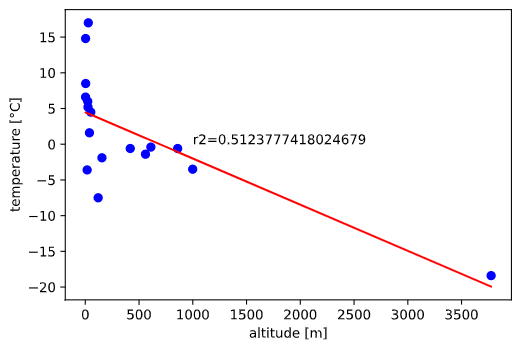
のようにうまく線形回帰できません。
気温には標高以外の要素(例えば緯度)も効いているようです。
そこで説明変数を緯度(latitude)とすると、
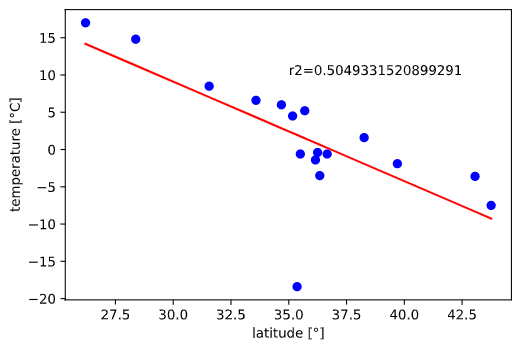
のように全体としては少し改善したように見えますが、
北緯36度付近(標高の高い地域が多い)の精度がイマイチであることがわかります。
精度が分かりやすいよう予測値と実測値をプロットしても、
import seaborn as sns
sns.regplot(lr.predict(X), y, ci=0, scatter_kws={'color':'blue'}) # 目的変数の予測値と実測値をプロット
plt.xlabel('pred_value') # 予測値
plt.ylabel('true_value') # 実測値
plt.text(0, -10, f'r2={r2_score(y, lr.predict(X))}') # R2乗値を表示
では標高と緯度を組み合わせて気温を推定するとどうなるでしょう?
感覚的には気温に効く2要素両方を考慮できるので、精度が上がると想像できます。
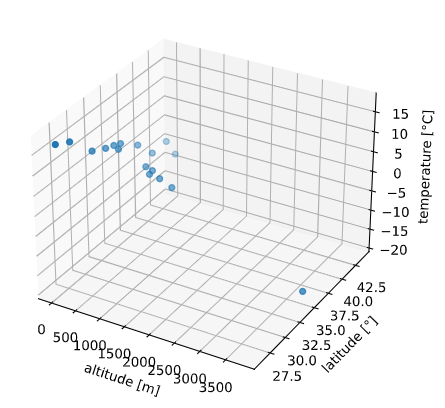
説明変数を標高(altitude)、緯度(latitude)の2次元として
(目的変数も合わせると3次元で)プロットしてみます
from mpl_toolkits.mplot3d import Axes3D
X = df_temp[['altitude', 'latitude']].values # 説明変数(標高+緯度)
y = df_temp[['temperature']].values # 目的変数(気温)
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter3D(X[:, 0], X[:, 1], y)
ax.set_xlabel('altitude [m]')
ax.set_ylabel('latitude [°]')
ax.set_zlabel('temperature [°C]')
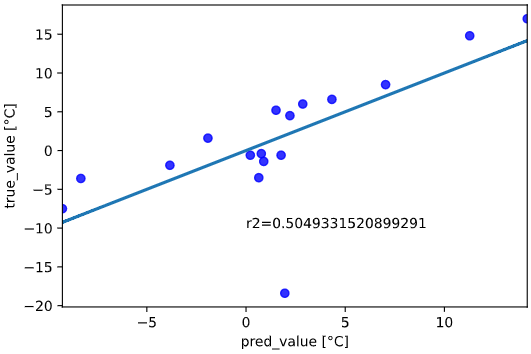
この2次元の説明変数で線形回帰、予測値と実測値をプロットすると
lr.fit(X, y) # 線形回帰実施
sns.regplot(lr.predict(X), y, ci=0, scatter_kws={'color':'blue'}) # 目的変数の予測値と実測値をプロット
plt.xlabel('pred_value [°C]')
plt.ylabel('true_value [°C]')
plt.text(0, -10, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
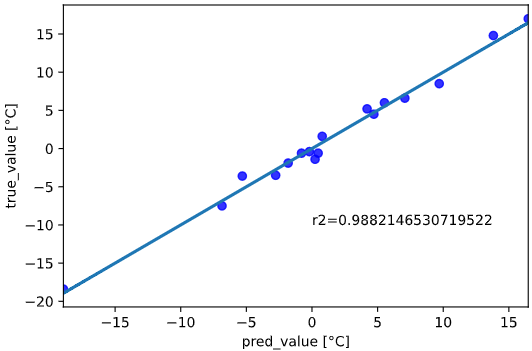
のように、予測精度が大きく向上する(ほぼ予測値≒実測値)ことが分かります。
以上のように、一般的に複雑な現象を予測したいときは、
多次元の説明変数を組み合わせることで、推定性能が向上することが多いです
※ただし、可視化難易度や次元の呪いなど、次元数が増えることによるデメリットもあるので、むやみに増やしすぎるのは禁物です
B. 非線形
サンプルとして使用するデータを変えます。
こちらを参考に、動物の体長と体重の関係をプロットしてみました。
name,body_length,weight
Mara,72,12
Lion,210,200
Hyena,150,70
Eland,295,650
Wolf,115,35
Hippopotamus,420,3000
Bear,150,115
Tiger,250,300
Deer,150,85
Camel,300,700
Zebra,220,275
Rhinoceros,425,2550
Buffalo,275,750
Elephant,675,6650
Gorilla,180,170
Giraffe,480,900
df_animal = pd.read_csv(f'./sample_data/animal_size.csv')
X = df_animal[['body_length']].values # 説明変数(体長)
y = df_animal[['weight']].values # 目的変数(体重)
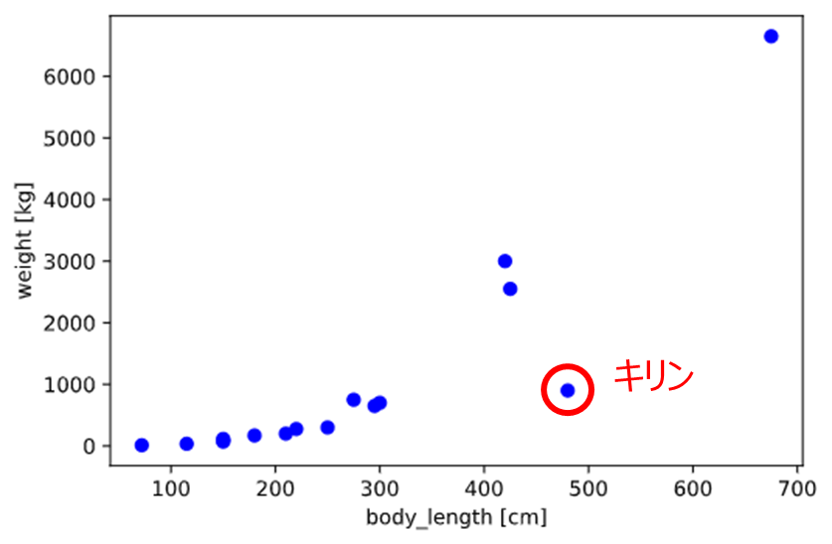
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.xlabel('body_length [cm]')
plt.ylabel('weight [kg]')
他の動物と明確に傾向の異なるキリン(細長い‥笑)を除外して線形回帰してみます
df_animal = df_animal[df_animal['name'] != 'Giraffe'] # キリンを除外
df_animal = df_animal.sort_values('body_length') # 表示用に体長でソート
X = df_animal[['body_length']].values # 説明変数(体長)
y = df_animal[['weight']].values # 目的変数(体重)
lr.fit(X, y) # 線形回帰実施
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('body_length [cm]')
plt.ylabel('weight [kg]')
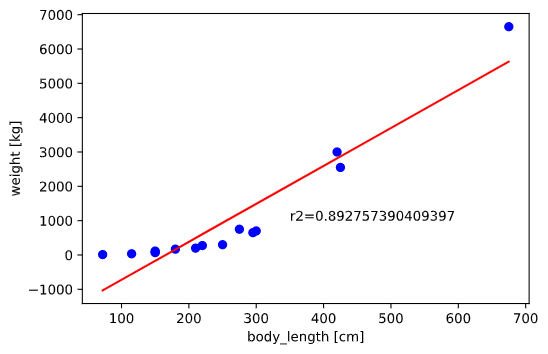
plt.text(350, 1000, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
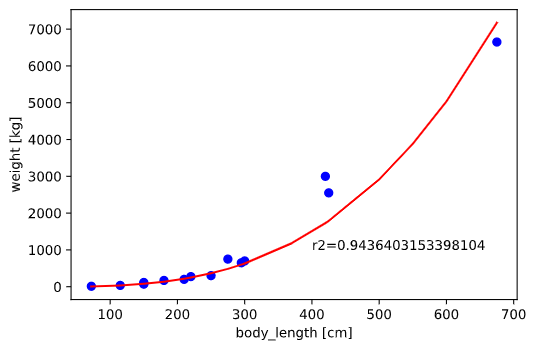
データの傾向としては体長が大きいほど体重増加の傾きが大きくなる、曲線的な増加をしていますが、
無理やり線形で回帰しているため、イマイチなフィッティングとなっています。
物理法則から、体重(∝体積)は体長の3乗に比例すると予測されるため、
3次式で回帰すれば(2次以上は「多項式回帰」と呼びます)、この**「曲線的な増加」**を表現できると想像できます。
多項式回帰の方法には、scikit-learnを使う方法や、scipy.optimizeを使う方法等がありますが、
今回は物理法則に基づいて3乗以外の係数を無視するため、scipy.optimizeを使用します。
def cubic_fit(x, a): # 回帰用方程式
Y = a * x **3
return Y
popt, pcov = curve_fit(cubic_fit, X[:,0], y[:,0]) # 最小二乗法でフィッティング
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
pred_y = cubic_fit(X, popt[0]) # 回帰線の作成
X_add = np.sort(np.vstack((X, np.array([[370],[500],[550],[600]]))), axis=0) # 線が滑らかになるよう、プロット用にデータ補完
pred_y_add = cubic_fit(X_add, popt[0]) # 回帰線の作成(プロット用)
plt.plot(X_add, pred_y_add, color = 'red') # 回帰線のプロット
plt.xlabel('body_length [cm]') # x軸のラベル
plt.ylabel('weight [kg]') # y軸のラベル
plt.text(400, 1000, f'r2={r2_score(y, pred_y)}') # R2乗値を表示
線形回帰と比べてフィッテングも良くなり、当てはまりの良さを表すR2値も向上していることが分かります。
3次式で非線形回帰したことで、推定性能が向上したと言えるでしょう!
上の例では「何乗に比例するか」を物理法則に基づき明示的に与えていますが、
実際の問題では明示的な式が分からない場合が多いです。
よく使われる機械学習アルゴリズムは、このような**非線形のフィッティングを「実データに合わせて」「柔軟に」**実現してくれる工夫が凝らされています(例:サポーベクターマシンにおけるカーネルトリック)
C. 汎化性能の向上(正則化)
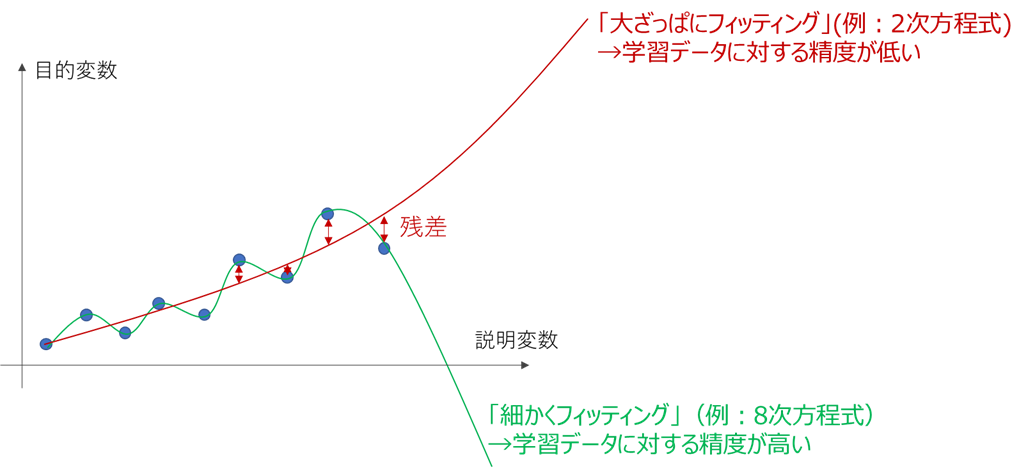
一般的にモデルを複雑にして細かい部分まで合わせ込むと、学習データに対する性能は向上します。
ただ上の図を見ると、細かくフィッティングした線は「合わせ込みすぎでは?」という印象を受けるかと思います。
この「学習データに過剰に合わせ込んだ状態」を、過学習(Overfitting)と呼びます。
過学習の弊害は、未知データに対する推定性能が落ちる事にあります。
下図のように、過学習すると学習データの細かな変化を鋭敏に拾いすぎてしまい、学習データが存在しない部分、すなわち未知データの推定能力が落ちてしまいます。
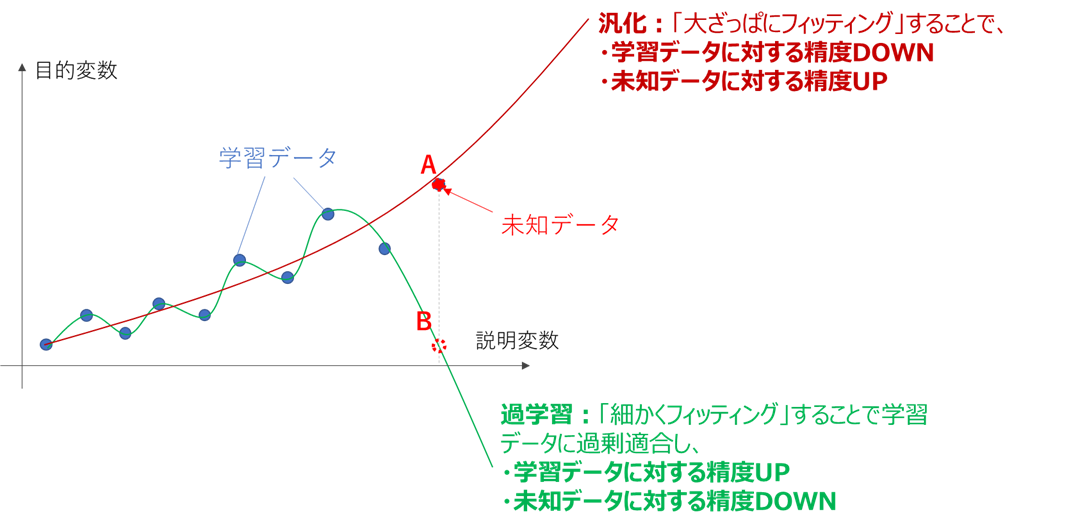
過学習防止に多用される手法が、正則化です(詳細は別記事で投稿しています)
機械学習は、一般的に学習データに対する損失関数(例:最小二乗法での誤差二乗和)を最小化するよう学習しますが、
これだけでは細かくフィッティングした複雑なモデルが生成され、過学習が起こります。
そこで、損失関数にモデルの複雑さを表す指標(正則化項)を加え、これを最小化するよう学習すれば、
性能と複雑さ、すなわち過学習と未学習のバランスを取った学習が実現できます。
このとき、元の損失関数と正則化項をどの割合で足し合わせるかで、上記のバランスが決まるのですが、
このバランス変化はSVMにおけるパラメータ「C」の挙動を見ると、分かりやすいかと思います。
1-3. ハイパーパラメータとは何か?
機械学習のアルゴリズムは、前記3種類(多次元・非線形・汎化性)を始めとした機能を実現するため様々な工夫を凝らしていますが、
「どれくらい非線形か」や「過学習と未学習」などのバランスは、実際のデータに合わせて学習とは別途調整する必要があります。
これらのバランスを調整するためのパラメータを、ハイパーパラメータと言います
サポートベクターマシンでの例
分類における定番アルゴリズムの1つである「サポートベクターマシン(SVM)」を例に、ハイパーパラメータの役割を解説します。
詳細は別記事に記載しておりますが、サポートベクターマシンにはgammaとCという2種類のハイパーパラメータがあり、それぞれ以下の役割を果たしています。
・gamma:カーネルトリックによる非線形決定境界の調整 → 「B.非線形」に対応する工夫
・C:正則化項(ソフトマージン)の調整 → 「C.汎化性能の向上(正則化)」に対応する工夫
gammaやCを変えた時の決定境界の変化を以下に図示します。
gammaを変化させたとき
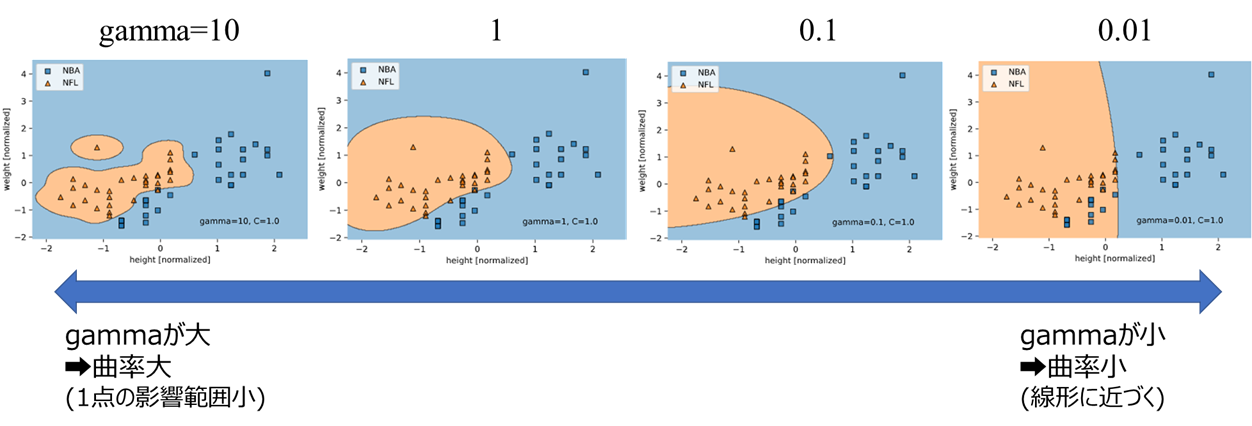
gammaが小さくなるほど曲率が小さくなって線形に近づき、gammaが大きくなるほど曲率が大きくなることが分かります。
ここからも、gammaが「どれくらい非線形か」を調整するパラメータであることが分かるでしょう
Cを変化させたとき
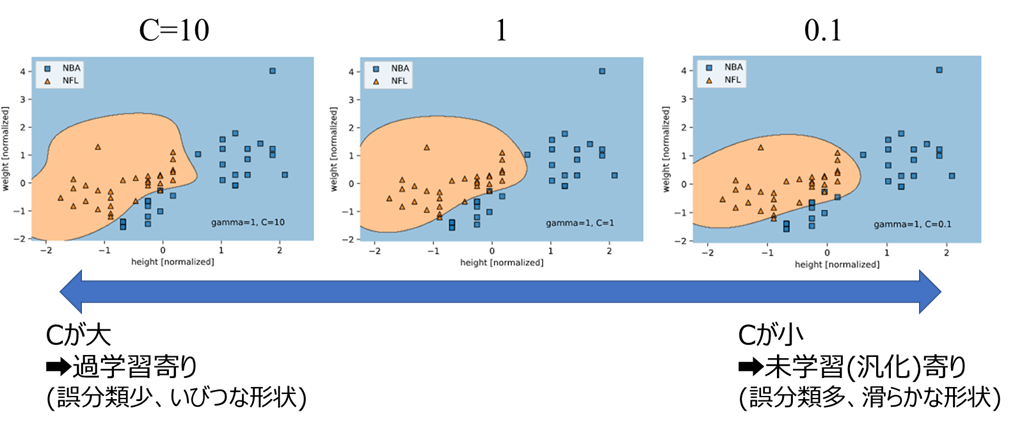
Cが大きいほど、誤分類は少ないがいびつな決定境界(過学習寄り)
Cが小さいほど、誤分類は多いが滑らかな決定境界(未学習=汎化寄り)
となっていることが分かります。
1-4. チューニングの目的
別記事に記載したSVMの例のように、機械学習は多種多様なアルゴリズムを通じて、「多次元」「非線形」「汎化性能」等の課題をクリアしています。
そして先人達の努力により、これらの課題は少数のハイパーパラメータに簡略化されて調整可能な形となっています(SVMではgammaとCの2個のパラメータ)
機械学習の性能をフル活用するためには、これらのパラメータを実際のデータに合わせチューニングする必要があります。
再現性のある調整をするためには、定量的な指標が必要となりますが、
分類:「誤分類の少なさ」を表す指標
回帰:「誤差の小ささ」を表す指標
となるような性能指標を最大化するようチューニングすることが、一般的な手法となります。
性能指標の具体例については、2章で解説します。
学習データとテストデータ
1-2-Cで触れましたが、下図のように学習データに対する性能指標を最大化しようとすると過学習状態となり、未知データに対する推定能力が低下します

機械学習の実運用時は、未知のデータに対する能力が重要となるので、これは喜ばしくない状況です。
この過学習を防ぐために、下図のように手持ちのデータを学習データとテストデータに分け、テストデータに対する性能指標を最大化するようパラメータチューニングを行うことが一般的です。
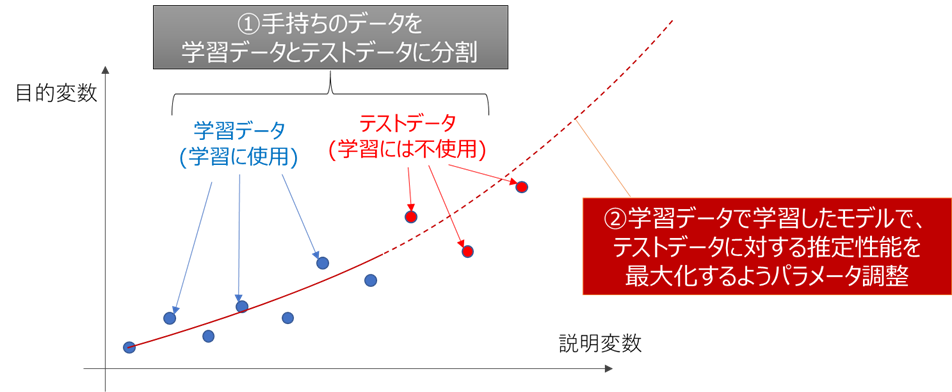
テストデータは学習に使用していないため、未知データに対する性能評価を模擬することができ、
過学習を防いで未知データに対する推定能力を上げることができます。
学習データとテストデータの分割法はクロスバリデーションと呼ばれる手法が一般的ですが、こちらも2章で解説します。
パラメータチューニングの目的
以上、パラメータチューニングの目的をまとめると、
ハイパーパラメータで非線形性や汎化性能のバランスを調整することで、未知データに対する推定性能を最大化する
となります
2. チューニングの手順とアルゴリズム一覧
前述のように、パラメータチューニングの手順を端的に言うと
データを学習データとテストデータに分け、
テストデータに対する性能指標を最大化するようチューニングする
となりますが、この手順をフローチャート化すると下図のようになります。
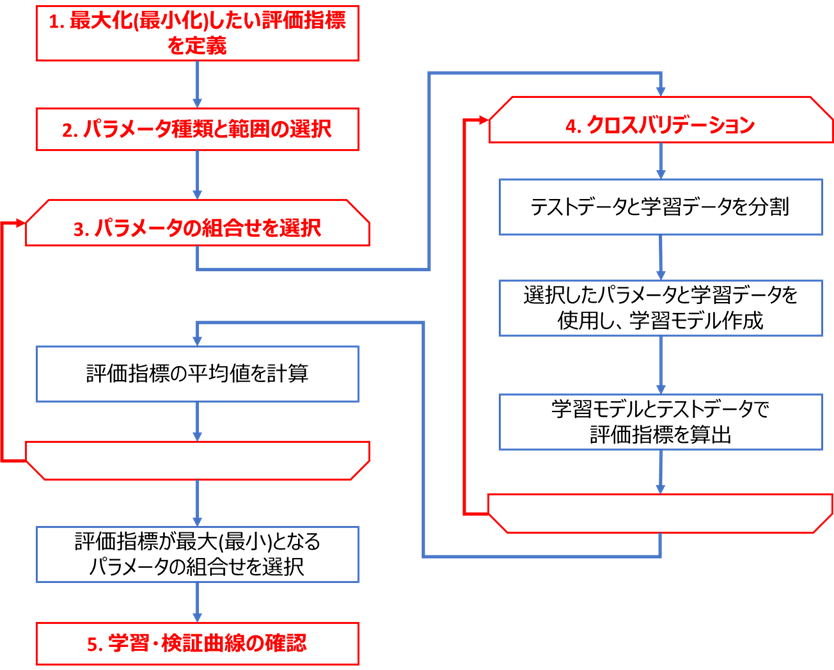
特に重要となる赤字部分に関して、詳細に解説します。
2.1 評価指標の定義
前述のように、評価指標は
分類:「誤分類の少なさ」を表す指標
回帰:「誤差の小ささ」を表す指標
を使用することが望ましいです。
分類、回帰それぞれについて、よく使われる指標とその特徴を列記します。
(scikit-learnで使用可能な指標一覧はこちら参照)
なお、これらの指標は、
大きい方が性能が良い指標:Accuracy、R2など
小さい方が性能が良い指標:RMSE、LogLossなど
の2種類が存在し、前者は最大化、後者は最小化する必要がある事にご注意ください
(scikit-learnでは後者は自動でマイナスを取ってくれるので、正負の方向をあまり気にしなくともチューニングができます)
A. 分類の評価指標
よく使われる分類の評価指標を列記します。
| 名称 | 和名 | scikit-learnでの名称 | 性能の良い方向 | メリット | デメリット |
|---|---|---|---|---|---|
| Accuracy | 正解率 | accuracy | 大きいほどGood | 適合率と再現率のバランスが見られる | 不均衡データに弱い |
| Precision | 適合率 (精度) | precision | 大きいほどGood | 偽陽性(見すぎ)を評価できる | Recallとトレードオフ |
| Recall | 再現率 | recall | 大きいほどGood | 見逃しを評価できる | Precisionとトレードオフ |
| F1-score | f1 | 大きいほどGood | 不均衡データに強い | PR-AUCより汎化性に劣る | |
| LogLoss | 交差エントロピー損失 | neg_log_loss | 小さいほどGood | 正誤の度合いを連続的に評価できる | 他データとの性能比較できず&確率算出が必要 |
| AUC | roc_auc | 大きいほどGood | 他データとの性能比較ができる | 計算量多い&確率算出が必要 | |
| PR-AUC | average_precision | 大きいほどGood | 不均衡データに強い | 計算量多い&確率算出が必要 |
どれがいいの?
基本:LogLoss
他データと性能比較したい場合:AUC
各クラスのデータ数偏り大(不均衡データ)※:PR-AUCまたはF1-score
多クラスかつ不均衡データ※:F1_macroまたはroc_auc_ovo
多クラスかつ不均衡でない:F1_microまたはroc_auc_ovr
※不均衡データのチューニング時は、分類器側にも引数「class_weight="balanced"」が必要です(参考)
その他指標選択時の諸注意は、こちらをご参照ください
####具体的な算出式
混同行列に基づき、下式で算出します。
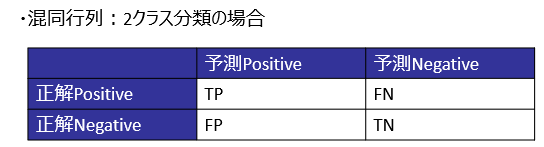
Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\\
Precision=\frac{TP}{TP+FP}\\
Recall=\frac{TP}{TP+FN}\\
F1=\frac{2\times Precision\times Recall}{Precision+Recall}\\
LogLoss=-\frac{1}{N}\sum_{i=1}^{N}\Bigl(y_i\log p_i +(1-y_i)\log(1-p_i)\Bigl)
※LogLossと確率
LogLossの式におけるpはそのクラスに所属する確率です。
クラス所属確率を算出できる分類手法はロジスティック回帰が代表的です。
scikit-learnでは前述のSVMにも確率を求めるメソッドがありますが、本来のSVMのアルゴリズムとは別に確率算出アルゴリズムを後付けで付加しているようです。
同様にscikit-learnの大半の分類アルゴリズムには、後付けの確率計算メソッド"predict_proba"があり、これらを利用してLogLossを算出できます。
私見となりますが、AccuracyやF1など分類の評価指標は離散的な値を取るものが多く、データ数が少ないとき多くのパラメータで評価指標が同値となり、真に性能が高いパラメータを見出すのが難しくなります。
一方でLogLossは連続的な値を取るため、データ数が少ない時もパラメータ間の性能差を鋭敏に評価できるため、多くのケースで推奨される指標なのだと思います。
※AUCとPR-AUCの算出式
基本的には、PrecisionとRecallはトレードオフ関係にあります。
このトレードオフの変化を見る手法として、ひとつは前述のF1-Score、もうひとつが下図のようなROC曲線です
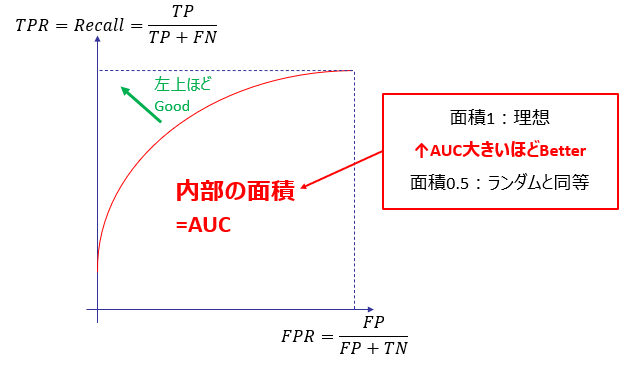
ROC曲線は、閾値を変化させて、TPR(見逃しの少なさ)とFPR(見すぎの多さ)の変化をプロットしたものとなります。
ROC曲線の内部の面積をAUCと呼び、前述のトレードオフを考慮した評価指標としてよく利用されます。
scikit-learnにおいては、LogLossのときと同様のクラス所属確率において、確率何%に閾値を引くかを変化させ、ROC曲線およびAUCを算出しています。
また、ROC曲線の代わりに、縦軸にPrecision、横軸にRecallをプロットしたPR曲線もあり、
PR曲線の内部の面積をPR-AUCと呼び、不均衡データの評価指標としてよく利用されます。
B. 回帰の評価指標
よく使われる回帰の評価指標を列記します(参考)
| 名称 | 和名 | scikit-learnでの指定法 | 性能の良い方向 | メリット | デメリット |
|---|---|---|---|---|---|
| R2-score | 決定係数 | r2 | 大きいほどGood | モデルの当てはまりの良さを見られる | 注意点4参照 |
| RMSE | 平均二乗誤差平方根 | neg_root_mean_squared_error | 小さいほどGood | 全データにバランスよくフィット | 外れ値の影響をやや受けやすい |
| MAE | 平均絶対誤差 | neg_mean_absolute_error | 小さいほどGood | 外れ値の影響を受けにくい | RMSEより最大誤差が大きくなる傾向 |
| RMSLE | 平均二乗対数誤差平方根 | neg_mean_squared_log_error | 小さいほどGood | 注意点3参照 | 正負に対し不公平な評価となる |
どれがいいの?
基本:RMSE
外れ値を無視したいとき:MAE
注意点3に該当するとき:RMSLE
その他指標選択時の諸注意は、こちらをご参照ください
####具体的な算出式
推定値\hat{y_i}\\
推定値の平均値\bar{y}\\
実測値y_i
に基づき、下式で算出します。
R2 = 1 -\frac{\sum_{i=1}^{n}\left(y_i - \hat{y_i}\right)^{2}}{\sum_{i=1}^{n}\left(
y_i - \bar{y} \right)^{2}}
RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}\left( y_i - \hat{y_i} \right)^{2}}
MAE = \frac{1}{n}\sum_{i=1}^{n}| y_i - \hat{y_i} |
RMSLE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}\left( log(y_i+1) - log(\hat{y_i}+1) \right)^{2}}
2.2 パラメータ種類と探索範囲の選択
「パラメータチューニングは経験が重要な職人芸」と言う人がいますが、
そう言われる所以のひとつがこの部分です。
例えば先述のSVMの場合、CとGammaという2つのパラメータを調整するのですが、
「Cは0.01~100の間、Gammaは0.0001~0.1の間」
というように、事前にパラメータの探索範囲を定義する必要があります
また、SVMはパラメータ数が2個ですが、XGBoostのように10個を超えるような場合、そのまま調整すると指数関数的に所要時間が増えるため、パラメータ種類を絞る必要があります。
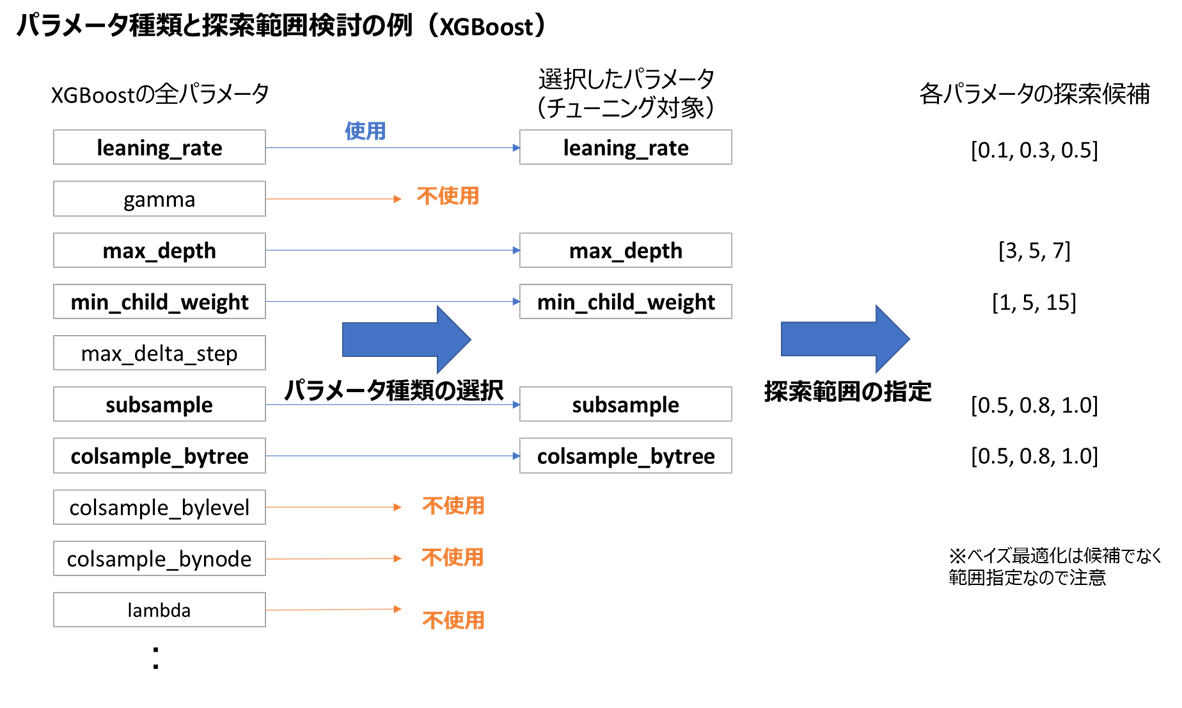
これらパラメータ種類と範囲の選択法に言及した書籍や記事は非常に少なく、経験に基づいて決める必要があります。
天下のgoogleさんも「すべてのケースに当てはまるアドバイスというのはほとんどありません」と言っています
私自身もこの工程に精通しているわけではないですが、以下の2通りの手法で、初心者でもある程度目星が付けられると考えています
先例の調査
他力本願な手法ですが(笑)、私の経験上、複数の先例を探してそれらの間をとって選択すれば、それなりに良い探索範囲を決められることが多かったです。
検証曲線
探索範囲指定に関しては、検証曲線を使用して目星をつけることができます(参考)
具体的な実装方法は後述します。
2.3 パラメータの組合せを選択
一般的に**「パラメータチューニング」**の手法として紹介されているのは、この部分です。
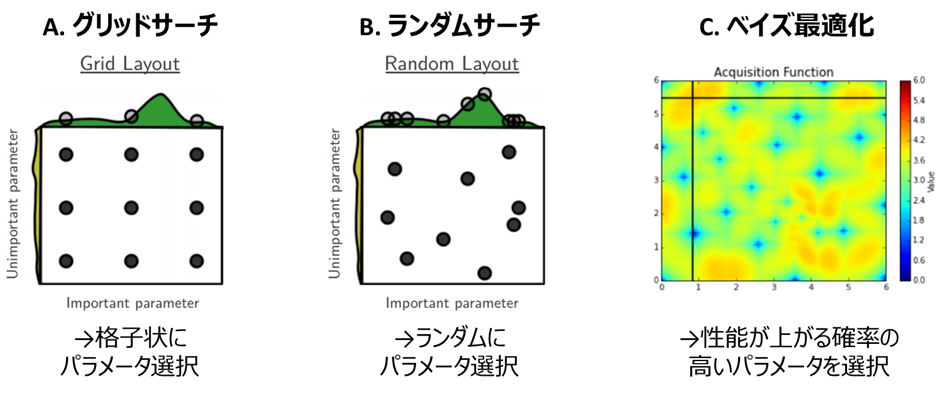
組合せの選択法には、主に下記3種類のアルゴリズムがあります。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | **グリッドサーチ ** | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
 |
|||||
| ※上記以外にも遺伝的アルゴリズム等があるが、機械学習用途ではあまり使用されない | |||||
| ※ランダムサーチの詳細および画像出典はこちら | |||||
| ※ベイズ最適化の画像出典 |
それぞれ具体的に解説します
A.グリッドサーチ
予め指定したパラメータの組合せを格子状に総当たりで走査します。
例えば、先ほど紹介したSVMの場合、gammaとCの2種類のパラメータが存在しますが、
gammaの組合せ = [0.01, 0.1, 1, 10]
Cの組合せ = [0.1, 1, 10]
を予め指定すると、以下の①~⑫のパラメータの組合せを総当たりで走査し、それぞれで2.1で指定した評価指標をクロスバリデーション(2.4で後述)で算出します。
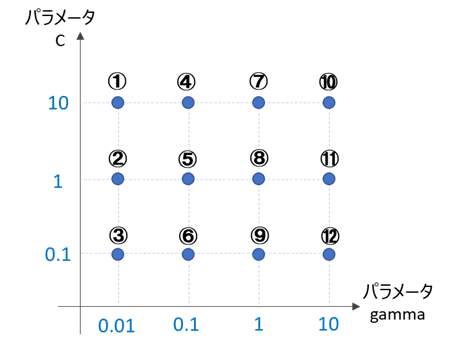
全ての組合せの中から評価指標が最も良いパラメータを採用すれば、チューニング完了となります。
グリッドサーチはパラメータの値を直接指定できるので、
解釈性の高さや経験を活かしやすいことが魅力です。
一方で、パラメータ数に対して組み合わせ数が指数関数的に増えるため、パラメータ数が多いXGBoostやLightGBMなどの学習器では非常に時間が掛かる事がデメリットです。
グリッドサーチのライブラリ
簡単なアルゴリズムなのでスクラッチでも実装できますが、Scikit-Learnにクロスバリデーションと一括で処理可能な"GridSearchCV"クラスがあるので、これを利用するのが便利かと思います
B.ランダムサーチ
ある範囲の中から、ランダムにパラメータの組合せを生成します。
scikit-learnでは下図のように、予め指定したパラメータの組合せから、ランダムに数点選びます。
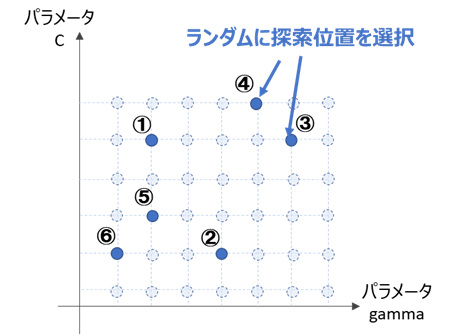
グリッドサーチと同様、選んだ数点のうち評価指標が最も良いパラメータを採用すれば、チューニング完了となります。
ランダムサーチは平均的にはグリッドサーチよりも効率よく探索が出来ると言われており、
チューニングの高速化が魅力です。
ランダムサーチのライブラリ
簡単なアルゴリズムなのでスクラッチでも実装できますが、Scikit-Learnにクロスバリデーションと一括で処理可能な"RandomizedSearchCV"クラスがあるので、これを利用するのが便利かと思います
C.ベイズ最適化
グリッドサーチは最初に決め打ちしたパラメータの組合せに左右され、ランダムサーチはランダムで探索するため、どちらも運任せ要素の強いアルゴリズムと言えます。
これに対しベイズ最適化は、前回までの評価結果を基に良いスコアの可能性が高い位置を推定し、次のパラメータの組合せとするため、前記探索法よりも根拠に基づいた効率的な探索ができるアルゴリズムと言えます。
ベイズ最適化のアルゴリズム
前述のように「良いスコアの可能性が高い位置」を推定する必要がありますが、
この推定に「ガウス過程」を使用します。ガウス過程とは、出力が入力を変数とした正規分布で表されるプロセスであり、その性質を利用して**「ガウス過程回帰」**と呼ばれる回帰手法に用いられています。
このガウス過程回帰の学習にベイズ推定を用いるため、「ベイズ最適化」と呼ぶようです。
ガウス過程回帰に関しては私も完全に理解しているわけではないので割愛しますが、
こちらやこちらで解説されており、厳密に理解されたい方は下記の書籍を購入するのが良いかと思います。
ガウス過程回帰の特徴に、出力として平均と標準偏差が得られる事が挙げられます。
詳細は後述しますが、この平均と標準偏差を使って「良いスコアの可能性が高い位置」を推定します。
また、ガウス過程以外にも、TPE (Tree-structured Parzen Estimator)と呼ばれる手法を用いた最適化が現在主流となりつつあるようです。
私は全く追えていませんが、こちらの記事で詳細に解説されています
獲得関数による探索位置の決定
「良いスコアの可能性が高い」ことを表す指標が、獲得関数(Acquisition Function)です。
ガウス過程回帰では目的変数予測値(ベイズ最適化の場合は2.1の評価指標予測値)の「平均」と「標準偏差」が求められますが、説明変数(ベイズ最適化の場合はチューニング対象のパラメータ)が1次元の場合の出力を図示すると以下のようになります。
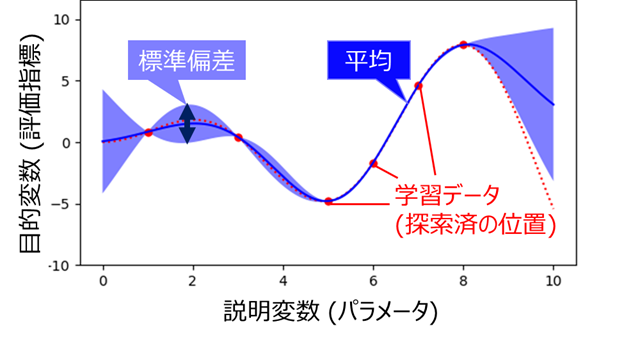
図を見ると、学習データ(探索済のパラメータ)の近傍では標準偏差が小さく、離れるほど標準偏差が大きくなることが分かります。
前者は正解が分かっている学習データの近くなので予測の確度が高い、後者は学習データから遠いので予測があいまい、と解釈すれば、感覚と一致するかと思います。
探索の方針として、予測平均が大きい位置を探す("活用"と呼びます)ことはもちろん重要なのですが、これだけだと現在の最大値付近を延々探し続けて局所解に陥ってしまうので、未知の部分 = 標準偏差が大きい位置を探す("探索"と呼びます)ことも重要となります。
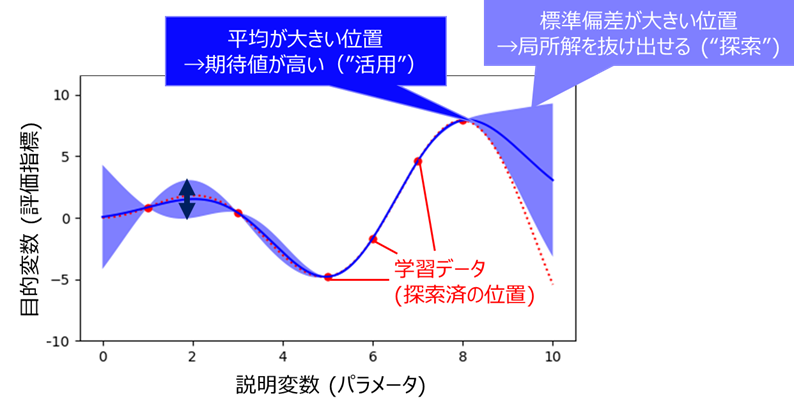
よって獲得関数は、平均と標準偏差を組み合わせる事により、"活用"と"探索"のバランスをとった関数とします。
獲得関数を決めるための方針としては、以下の3種類があります
(各方針での具体的な計算法はこちらが分かりやすいです)
| 名称 | 概要 | 特徴 |
|---|---|---|
|
PI (Probability of Improvement) |
現在の最大値を超える確率が最も高い点を選ぶ | 局所解に陥りやすい |
|
EI (Expected Improvement) |
現在の最大値との差の期待値が最も高い点を選ぶ | バランスが良い |
|
UCB (Upper Confidence Bound) |
上側信頼区間が最も高い点を選ぶ | EIと近い傾向 |
| ※こちらを参考にさせて頂きました |
それぞれの探索法を簡単に解説します。
・PI (Probability of Improvement)
現在の最大値を超える確率が最も高い点を選ぶ方法です。
下図のようなイメージで獲得関数を求めます
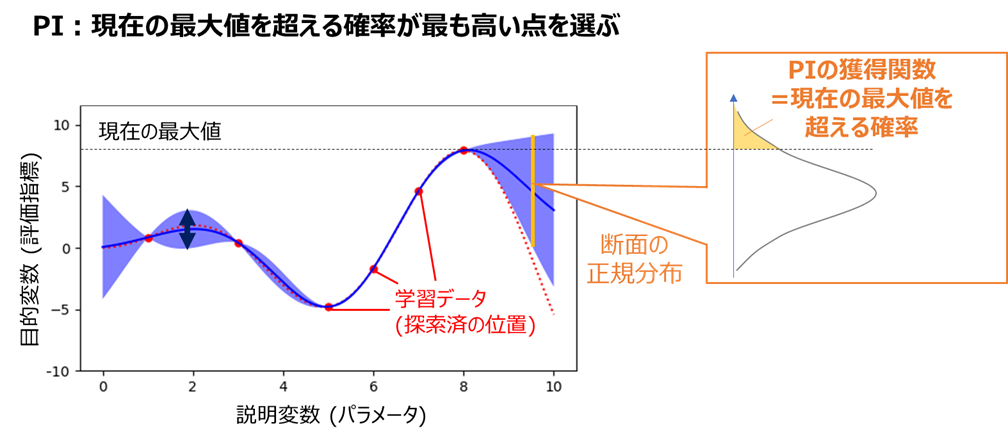
PIは他の手法よりも"活用"が重視されるため、現在の最大値付近を集中探索しがちで、局所解に陥りやすいと言われています
・EI (Expected Improvement)
うまく表現できるグラフが思い付かなかったので図は割愛しますが。
現在の最大値との差の期待値が最も高い点を選びます。
PIよりも局所解に陥りづらいと言われています。
・UCB (Upper Confidence Bound)
現在の最大値を超える確率が最も高い点を選ぶ方法です。
下図のようなイメージで獲得関数を求めます(上側信頼区間は1σや95%信頼区間等を指定)
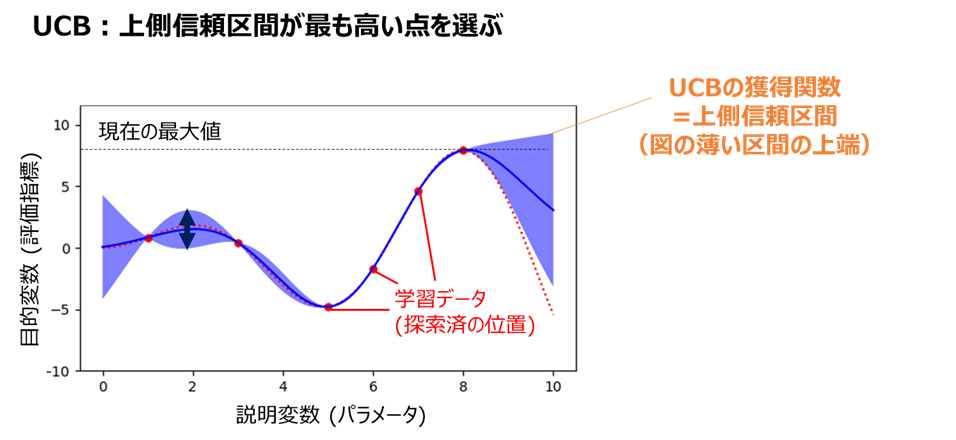
UCBはEIと似た傾向の探索となると言われています。
BayesianOptimizationライブラリでは、このUCBがデフォルトとなっています。
パラメータ2個におけるベイズ最適化のGifアニメ
ベイズ最適化の進行イメージがつかみやすいよう、
BayesianOptimizationライブラリ公式より、平均(Gausian Process Predicted Mean)と標準偏差(Gausian Process Variance)からUCB方針で求めた獲得関数(Acquisition Function)のGifアニメを下記します。
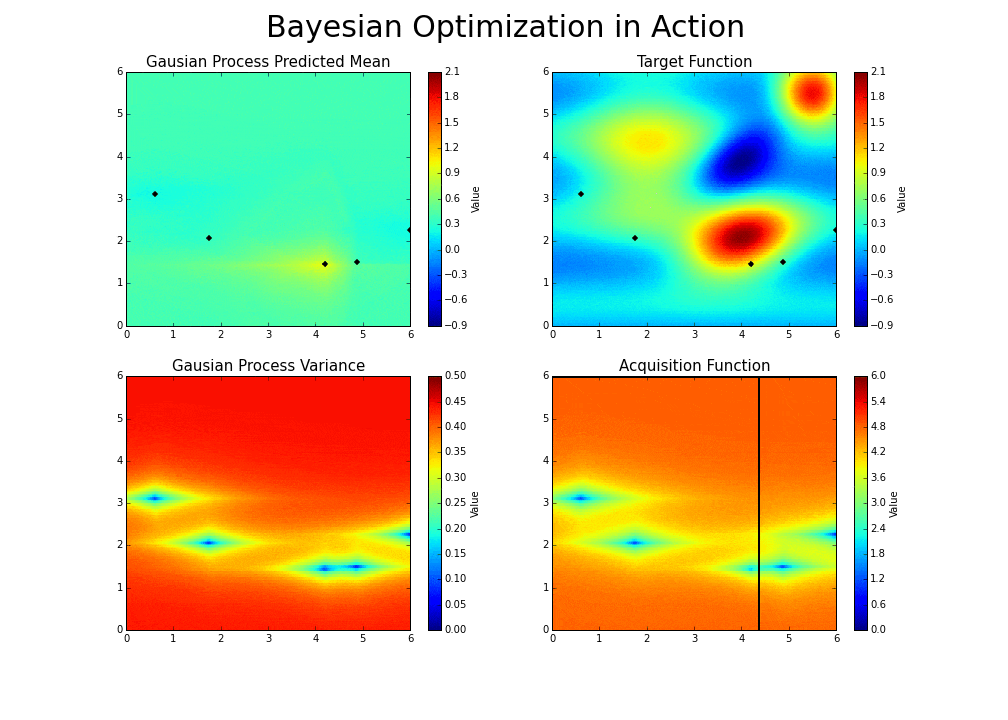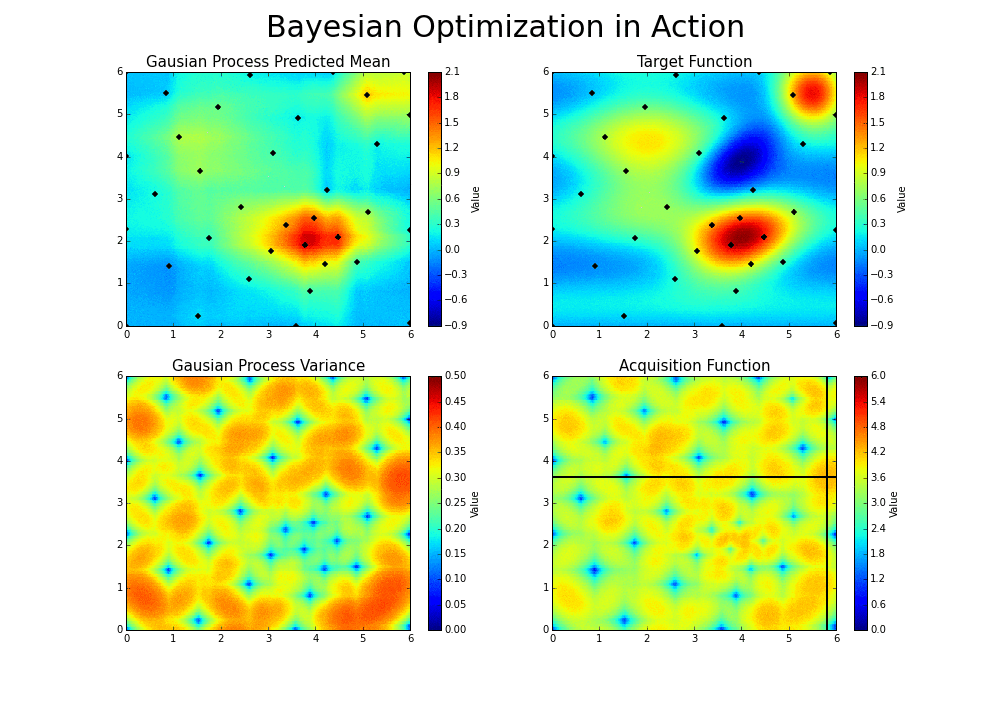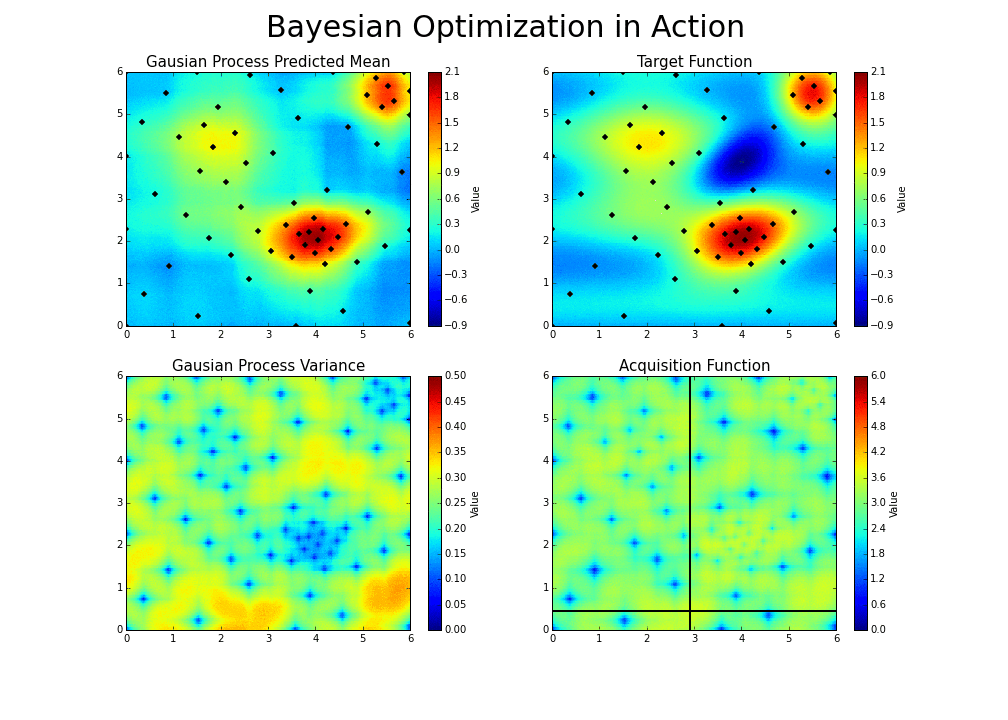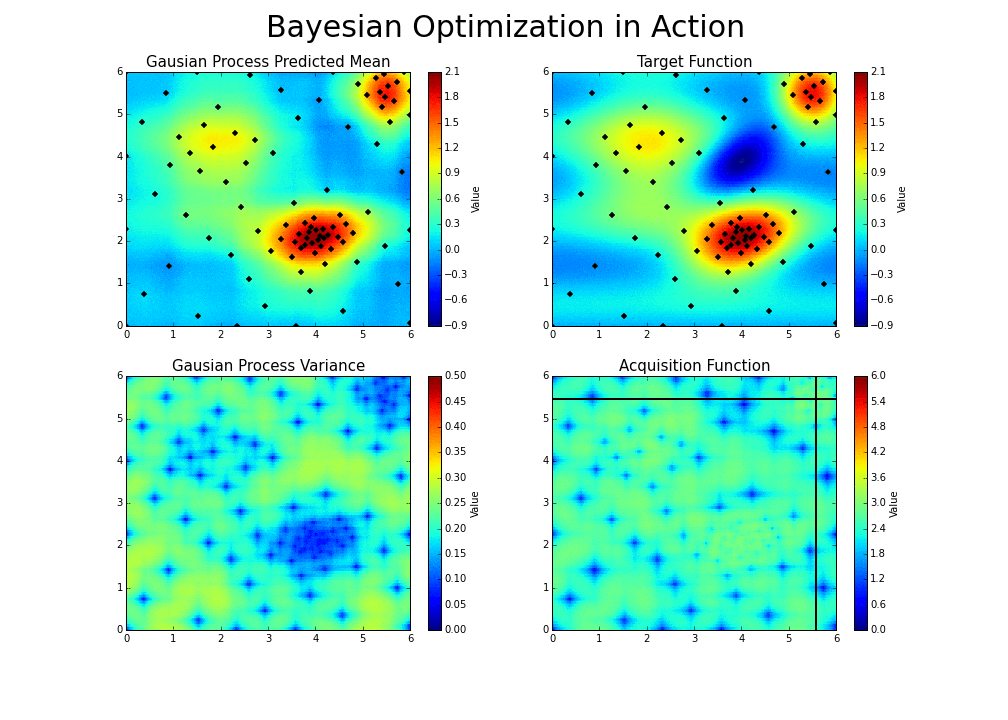
探索済データ(黒い点)が近くになく、かつ平均値が高そうな部分でAcquisition Functionが大きくなっていることが分かるかと思います。
また、BayesianOptimizationではベイズ最適化に入る前に、最初に複数の初期点(点の数を引数"init_points"で指定)をランダム生成し、ここから探索をスタートします。
ベイズ最適化は局所解に陥らないための工夫が随所にあるとはいえ、初期値に依存してある程度の局所解に陥ってしまうことは往々にしてあるため、これを防ぐための工夫となっています(init_pointsが小さすぎると局所解に陥りやすい)
ベイズ最適化のライブラリ
いくつかありますが、BayesianOptimization(GitHub Star=5100)とOptuna(GitHub Star=4500)が代表的です。どちらも使い方が少し複雑なので、後述します
| ライブラリ名 | 使用アルゴリズム | その他特徴 |
|---|---|---|
| BayesianOptimization | ガウス過程回帰(BO-GP) | |
| Optuna | TPE | 枝刈りによる高速化、国産 |
| ※ほかにもHyperopt等が有名ですが、Optunaと方式が近いため割愛します |
2.4 クロスバリデーション
パラメータチューニングのためには、学習データとテストデータを分割する必要がありますが、
最も一般的な分割法として、データをN等分した上で、1つのグループをテストデータとし、残りを学習データとするクロスバリデーションが挙げられます。
クロスバリデーションの分割イメージは、下のWikipediaの図が分かりやすいです

Nの値ですが、5、あるいは10が使われることが多いです。
目安としては、
データ数が少ない場合、少しでも学習データの数を稼ぐためにNの値を大きくする
データ数が多すぎる場合は、計算量を減らすためにNの値を小さくする
傾向があります。
具体的にどのように分割するかは、多数の方法がありますが、よく使うものを解説します。
| 手法名 | よく使うシチュエーション |
|---|---|
| KFold | 基本 |
| Stratified KFold | データ数少ない分類orクラス間の偏り大 |
| Leave One Group Out | 検証データと同グループを学習データに含めたくない時 |
| Time Series Split | 時系列データ |
なお、いずれの手法でも各テストデータで求めた評価指標の平均値(N=5のとき、5個別々に求めた指標の平均値)を最終的な評価指標として採用し、「2.3 パラメータ選択」のループに戻します
KFold
最も基本的な分割法で、データの先頭から順番にN等分、あるいはランダムにN等分します
Stratified KFold
通常のKFoldだと、データ数が少なかったりクラス間のN数の偏りが大きかったりすると、分割内に特定のクラスが含まれない場合が発生し、意味のある評価が出来なくなってしまうことがあります。
このような場合、全体でのクラス数の割合を維持したまま分割を行う「Stratified KFold」が有効です。
Leave One Group Out (LOGO)
データをラベルに基づいてグルーピングし、ある1グループをテストデータとして残りのグループを学習データとする「Leave One Group Out (LOGO)」という方法があります。
例えば実験データに基づいて予測をしたい場合、繰り返し精度を図るために同条件で複数回実験をしたデータを取得する場合が多いかと思いますが、ランダムに分割するとテストデータと同条件のデータが学習データに含まれてしまうため、性能が過大評価されていまいます。
このようなとき、条件ごとにグルーピングしてLOGOで分割すれば、同条件のデータが学習データに含まれないので、公平な性能評価を実現する事ができます。
似た手法として、LOGOのグループのうち複数を統合してクロスバリデーションするGroup KFoldもあります。
Time Series Split
時系列データの場合、基本的には過去のデータを学習データ、未来のデータをテストデータとして分割する必要があります。
これは、未来の情報を使ってモデルを学習する事が実運用上は不可能であるため、未来の情報が学習データに混入して性能が過大評価される「データリーク」を防ぐためです。
データリークを防ぎつつクロスバリデーションするための方法が、Time Series Splitです。
詳しくはこちらが参考になるかと思います
Leave One Out
極端な例としては、N=全データ数とし、テストデータが常に1個となるような「Leave One Out」という分割法もあります。こちらの記事でも性能評価に採用したように、データ数が少ない場合に学習データの数を稼ぐ上で有効な手法ですが、パラメータチューニング用途では過学習しやすく一般的に利用されません。
##2-5 学習・検証曲線の確認
1-3でも述べましたが、機械学習において最大の敵のひとつが過学習です。
パラメータチューニングもこの過学習を防ぐための手法のひとつですが、
チューニング後に過学習していないかを、**「学習曲線」「検証曲線」**というグラフで確認可能です
学習曲線の確認
学習曲線とは、横軸に学習データ数(サンプルサイズ)、縦軸にテストデータ(検証データ)および学習データから算出した評価指標をプロットしたグラフです。
学習曲線により、
・目的の性能を達成しているか?(バイアスが十分低いか)
・過学習を起こしていないか?(バリアンスが十分低いか)
が確認できます。
・確認方法
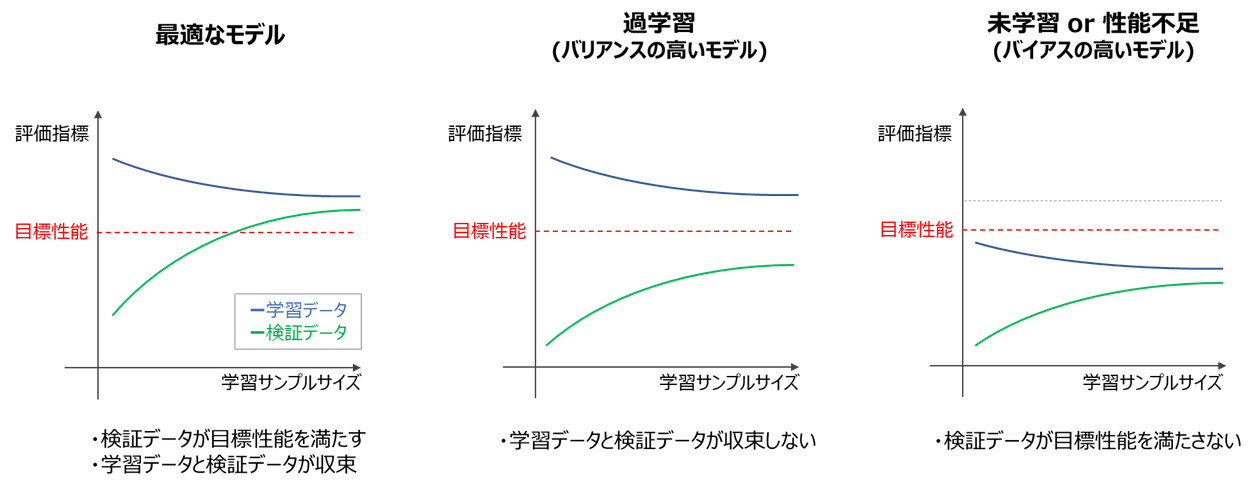
一般的に学習曲線は、以下のような形状となることが多いです。
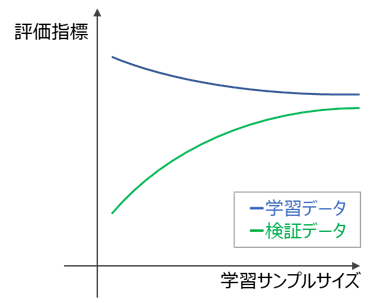
この図において、
・目的の性能を達成しているか → 検証データ指標が目標性能を上回っているか
・過学習していないか → 検証データ指標と学習データ指標が収束しているか
なお、バイアスに関しては目標性能が定められていない場合、明確な判断が難しいため、
課題に応じて柔軟に対応してください。
検証曲線の確認
検証曲線とは、横軸に調整対象のパラメータ、縦軸にテストデータ(検証データ)および学習データから算出した評価指標をプロットしたグラフで、パラメータごとに別個にプロットされます(3個のパラメータがあれば3個の検証曲線がプロットされる)
検証曲線により、
・性能の極大値を捉えられているか?
・過学習していないか?
が確認できます。
・確認方法
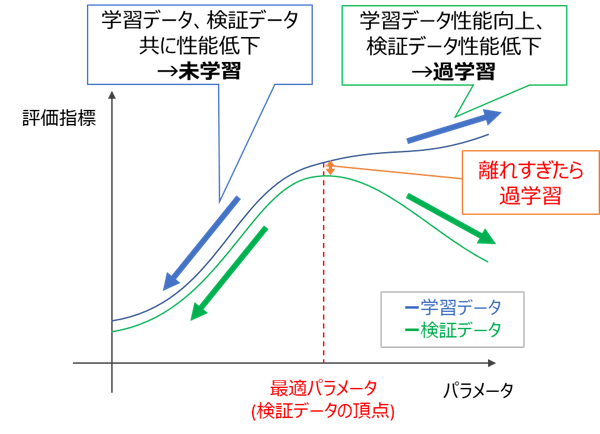
一般的に検証曲線は、以下のような形状となることが多いです。
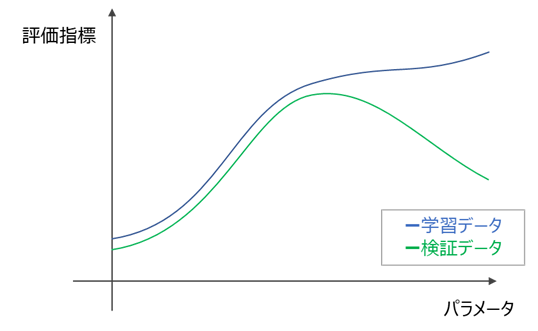
この図において、
・性能の最大値を捉えられているか → 最適パラメータが検証データ指標の頂点に来ているか
・過学習していないか → 最適パラメータにおいて学習データ指標と検証データ指標が離れすぎていないか
探索履歴の可視化
パラメータ数が2個のときしか使えませんが、ヒートマップや散布図で探索点およびそのときの評価指標が可視化できます。
・ヒートマップ(グリッドサーチの探索点)
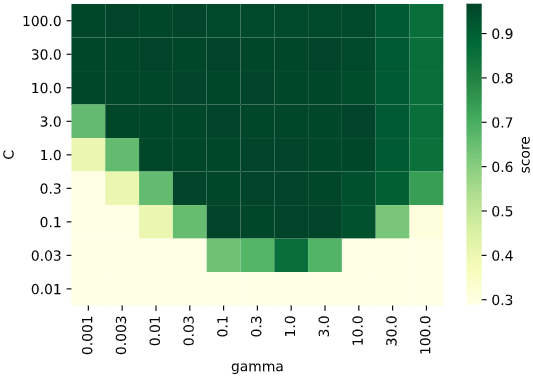
・散布図(ランダムサーチ、ベイズ最適化の探索点)
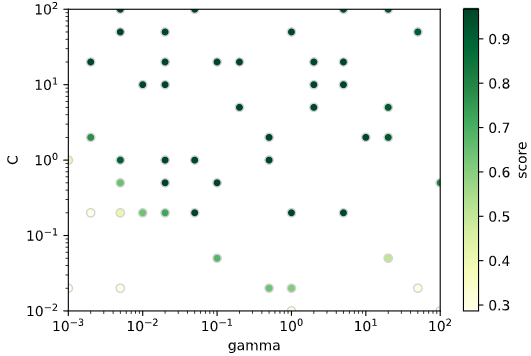
パラメータ4個くらいまでなら、複数のヒートマップ・散布図で分割し、無理やり描画することも可能かと思います
(後日記事にします)
3.実装
パラメーチューニングを実際に実装した例を紹介します。
今回は以下の4パターン(No3, 4は別記事で投稿するので暫しお待ちください)
での実装例となります。
| No. | 機械学習アルゴリズム | 問題の種類 | クロスバリデーション手法 | 注意点 |
|---|---|---|---|---|
| 1 | SVM | 多クラス分類 | KFold | |
| 2 | 標準化+SVM (パイプライン) |
2クラス分類 | Stratified KFold | |
| 3 | XGBoost | 回帰 | KFold | 別記事 |
| 4 | LightGBM | 回帰 | KFold | 別記事 |
3.1 サポートベクターマシン分類
irisデータセットをSVMで分類するモデルを、パラメータチューニングしてみます。
チューニング前のモデルの確認
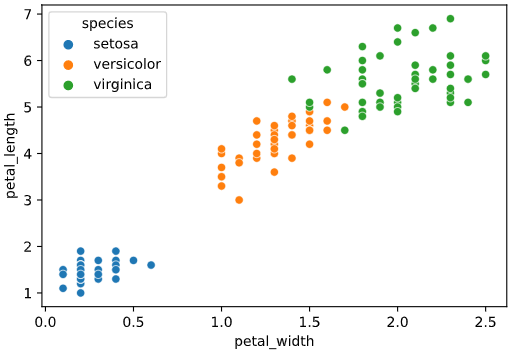
irisデータセットを読み込み、"petal_width", "petal_length"を特徴量として可視化してみます
import seaborn as sns
iris = sns.load_dataset("iris")
sns.scatterplot(x='petal_width', y='petal_length', data=iris, hue='species')
チューニング前のモデルをこちらのツールを使って3分割クロスバリデーションで可視化します
(通常は5分割クロスバリデーションが多いですが、今回は図が増えすぎないよう3分割します)
from seaborn_analyzer import classplot
from sklearn.svm import SVC
from sklearn.model_selection import KFold
# モデル作成
model = SVC() # チューニング前のモデル(パラメータ指定しない)
# クロスバリデーションして決定境界を可視化
seed = 42 # 乱数シード
cv = KFold(n_splits=3, shuffle=True, random_state=seed) # 3分割KFoldでクロスバリデーション分割指定
classplot.class_separator_plot(model, ['petal_width', 'petal_length'], 'species', iris,
cv=cv, display_cv_indices=[0, 1, 2])
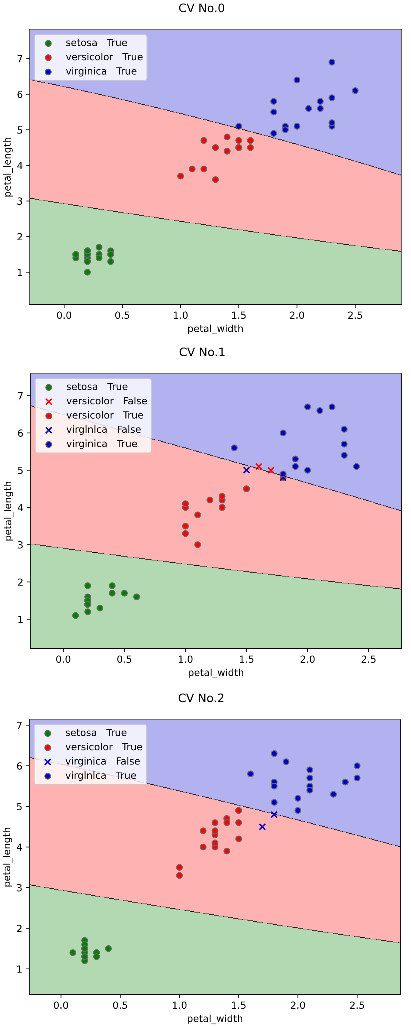
デフォルトでもいい感じで分類できていそうですが‥(笑)
ひとまずチューニングを続けていきます。
※なお、通常SVMはスケールを揃えるため事前に標準化を実行する必要がありますが、今回の特徴量はどちらもcm単位でスケールが揃っているため、標準化未実施で処理を進めていきます
手順1 最大化したい評価指標の定義
今回は
・多クラス分類
・不均衡データではない
ので、2.1のフローに基づき"f1_micro"を採用します。
チューニング前の評価指標をクロスバリデーションで算出します。
from sklearn.model_selection import cross_val_score
import numpy as np
X = iris[['petal_width', 'petal_length']].values # 説明変数をndarray化
y = iris['species'] # 目的変数をndarray化
scoring = 'f1_micro' # 評価指標をf1_microに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
scores=[1. 0.92 0.96]
average_score=0.96
このクロスバリデーションで求めたスコアの平均値average_scoreが、パラメータチューニングで向上させたい指標となります。
また、パラメータのうちgammaはこちらのgamma='scale'のときの式で動的に計算されるので、
参考値として計算しておきます。
print(f'gamma = {1 /(X.shape[1] * X.var())}')
gamma = 0.14396727220794353
今回のデータではデフォルトのgamma≒0.144であることがわかります
手順2 パラメータ種類と範囲の選択
・種類
SVMにはgammaとCの2種類のパラメータしか存在しないので、どちらもチューニング対象として採用します。
・範囲
適当な初期範囲を定めて検証曲線をプロットし、その結果に基づいて範囲を調整していきます
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
cv_params = {'gamma': [0.01, 0.03, 0.1, 0.3, 1, 3, 10],
'C': [0.1, 0.3, 1, 3, 10]}
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale('log')
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
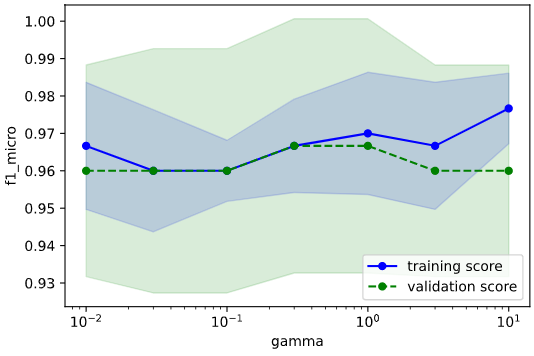
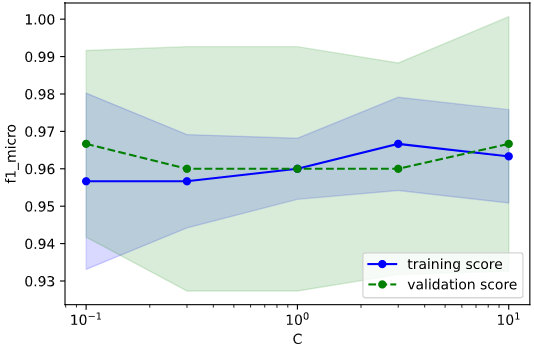
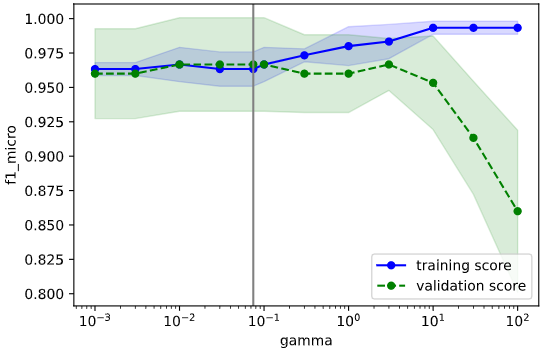
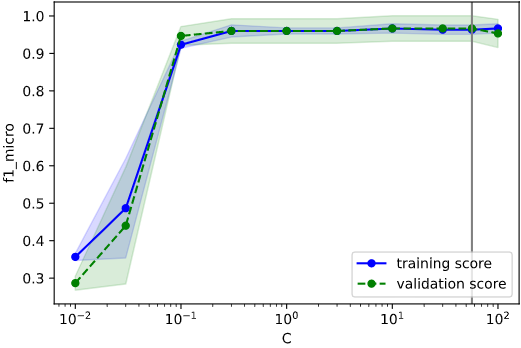
gamma, C共に変化に乏しく、パラメータに対する指標の傾向を掴めていないので、範囲を広げて再描画してみます。
cv_params = {'gamma': [0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 100, 1000],
'C': [0.001, 0.01, 0.1, 0.3, 1, 3, 10, 100, 1000]}
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale('log')
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
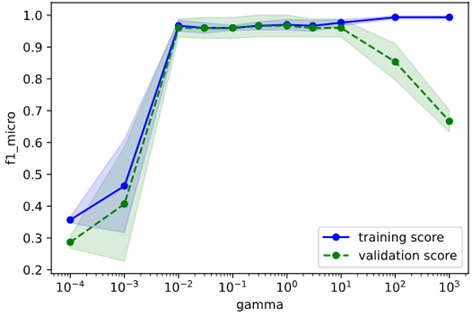
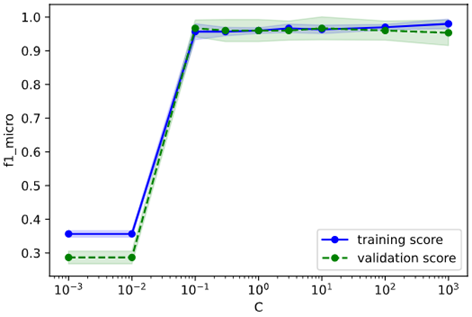
下図のように、どちらのパラメータも過学習、未学習の傾向がつかめている事が分かります。
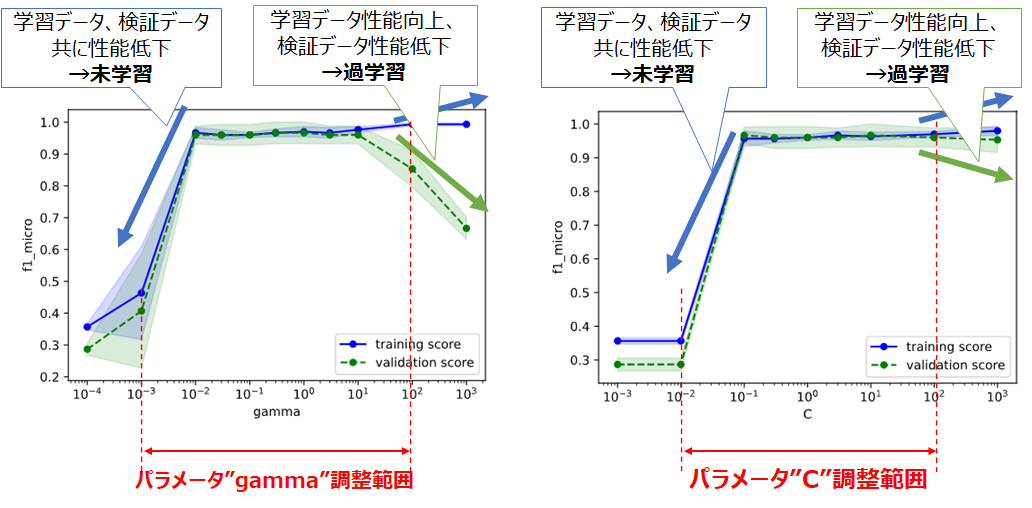
今回は未学習・過学習の小さい範囲よりも少し広めにとって、
パラメータ"gamma":0.001~100
パラメータ"C":0.01~100
を調整範囲とすることとします。
手順3&4 パラメータ選択&クロスバリデーション
パラメータ選択とクロスバリデーションはループで一括実行するため、まとめて解説します。
2.3で解説した以下A~Cの手法から1つ方法を選択してください。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | **グリッドサーチ ** | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
| A、B、C (BayesianOptimization)、C (Optuna)の4種類の実装法をそれぞれ解説します。 |
グリッドサーチの場合
グリッドサーチでの実装法を解説します
Scikit-Learnにはグリッドサーチとクロスバリデーションを一括実行する、GridSearchCVという便利なクラスがあるので、これを利用します
from sklearn.model_selection import GridSearchCV
# 最終的なパラメータ範囲
cv_params = {'gamma': [0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100],
'C': [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]}
# グリッドサーチのインスタンス作成
gridcv = GridSearchCV(model, cv_params, cv=cv,
scoring=scoring, n_jobs=-1)
# グリッドサーチ実行(学習実行)
gridcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = gridcv.best_params_
best_score = gridcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
なお、引数"n_jobs"は並列動作する最大スレッド数を指定するもので、「-1」を指定すると全てのプロセッサを使用し、通常よりも高速なチューニングが可能となります。
最適パラメータ {'C': 0.1, 'gamma': 0.1}
スコア 0.9666666666666667
C=0.1, gamma=0.1のときに評価指標f1_microが最大となり、その時の値は0.966‥であることが分かります
グリッドサーチで選択したパラメータと、算出した評価指標との関係をヒートマップで表示します。
import pandas as pd
# パラメータと評価指標をデータフレームに格納
param1_array = gridcv.cv_results_['param_gamma'].data.astype(np.float64) # パラメータgamma
param2_array = gridcv.cv_results_['param_C'].data.astype(np.float64) # パラメータC
mean_scores = gridcv.cv_results_['mean_test_score'] # 評価指標
df_heat = pd.DataFrame(np.vstack([param1_array, param2_array, mean_scores]).T,
columns=['gamma', 'C', 'test_score'])
# グリッドデータをピボット化
df_pivot = pd.pivot_table(data=df_heat, values='test_score',
columns='gamma', index='C', aggfunc=np.mean)
# 上下軸を反転(元々は上方向が小となっているため)
df_pivot = df_pivot.iloc[::-1]
# ヒートマップをプロット
hm = sns.heatmap(df_pivot, cmap='YlGn', cbar_kws={'label': 'score'})
※グリッドサーチをスクラッチ実装
参考までに、グリッドサーチおよびクロスバリデーションをスクラッチ実装した場合のコードを下記します。
GridSearchCVクラスも、内部的には同様の処理をしています。
import numpy as np
from sklearn.metrics import check_scoring
# パラメータ総当たり配列(グリッド)を作成
param_tuple = tuple(cv_params.values())
param_meshgrid = np.meshgrid(*param_tuple)
param_grid = np.vstack([param_array.ravel() for param_array in param_meshgrid]).T
# パラメータと評価指標格納用list
param_score_list = []
# グリッドを走査(スクラッチ実装)
for param_values in param_grid:
# パラメータをdict型にしてモデルに格納
params = {k: v for k, v in zip(cv_params.keys(), param_values)}
model.set_params(**params)
# クロスバリデーション(スクラッチ実装)
scores = [] # 指標格納用リスト
for train, test in cv.split(X, y):
# 学習データとテストデータ分割
X_train = X[train] # 学習データ目的変数
y_train = y[train] # 学習データ説明変数
X_test = X[test] # テストデータ目的変数
y_test = y[test] # テストデータ説明変数
# モデルの学習
model.fit(X_train, y_train)
# 指標算出
scorer = check_scoring(model, scoring)
score = scorer(model, X_test, y_test)
scores.append(score)
# 指標の平均値を算出
mean_score = np.mean(scores)
# パラメータと指標をlistに格納
param_score_list.append({'score': mean_score,
'params': params})
# 最適パラメータの表示と保持
max_index = np.argmax([a['score'] for a in param_score_list])
best_params = [a['params'] for a in param_score_list][max_index]
best_score = [a['score'] for a in param_score_list][max_index]
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'C': 0.1, 'gamma': 0.1}
スコア 0.9666666666666667
GridSearchCVを使った場合と同じ結果になっていることが分かります
ランダムサーチの場合
ランダムサーチでの実装法を解説します
Scikit-Learnにはランダムサーチとクロスバリデーションを一括実行する、RondomizedSearchCVという便利なクラスがあるので、これを利用します
from sklearn.model_selection import RandomizedSearchCV
# パラメータの密度をグリッドサーチのときより増やす
cv_params = {'gamma': [0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100],
'C': [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100]}
# ランダムサーチのインスタンス作成
randcv = RandomizedSearchCV(model, cv_params, cv=cv,
scoring=scoring, random_state=seed,
n_iter=50, n_jobs=-1)
# ランダムサーチ実行(学習実行)
randcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = randcv.best_params_
best_score = randcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
引数"n_iter"は、パラメータ選択の繰り返し回数です。50を指定した場合、パラメータ空間上でランダムに選んだ50点を探索します。
また、探索候補点を増やすため、パラメータの密度(リスト内の要素数)はグリッドサーチのときも増やしてください(等間隔でリスト生成したい場合range関数を、Logスケールのパラメータで等比数列的に作成したい場合はnp.logspace関数を使うと便利です)
最適パラメータ {'gamma': 1, 'C': 0.2}
スコア 0.9666666666666667
C=0.2, gamma=1のときに評価指標f1_microが最大となり、その時の値は0.966(グリッドサーチのときと同じ)であることが分かります
ランダムサーチで選択したパラメータと、算出した評価指標との関係を散布図で表示します。
# パラメータと評価指標をndarrayに格納
param1_array = randcv.cv_results_['param_gamma'].data.astype(np.float64) # パラメータgamma
param2_array = randcv.cv_results_['param_C'].data.astype(np.float64) # パラメータC
mean_scores = randcv.cv_results_['mean_test_score'] # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(np.amin(cv_params['gamma']), np.amax(cv_params['gamma'])) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(np.amin(cv_params['C']), np.amax(cv_params['C'])) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('gamma') # X軸ラベル
plt.ylabel('C') # Y軸ラベル
ベイズ最適化(BayesianOptimization)の場合
BayesianOptimizationによるベイズ最適化の実装法を解説します
BayesianOptimizationにはGridSearchCVのようなランダムサーチとクロスバリデーションを一括実行するメソッドは存在せず、クロスバリデーションによる評価指標算出メソッドを自作する必要があります。
まずは、BayesianOptimizationの仕様に基づき素直に実装してみます。
from bayes_opt import BayesianOptimization
# パラメータ範囲(Tupleで範囲選択)
bayes_params = {'gamma': (0.001, 100),
'C': (0.01, 100)}
# ベイズ最適化時の評価指標算出メソッド
def bayes_evaluate(gamma, C):
# 最適化対象のパラメータ
params = {'gamma': gamma,
'C': C}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params, random_state=seed)
bo.maximize(init_points=5, n_iter=30, acq='ei')
# 最適パラメータの表示と保持
best_params = bo.max['params']
best_score = bo.max['target']
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'C': 22.99030591883568, 'gamma': 0.09158261877377644}
スコア 0.9666666666666667
ランダムサーチのときと同様、探索履歴を散布図で可視化します。
# パラメータと評価指標をndarrayに格納
df_history = pd.DataFrame(bo.space.params, columns=bo.space.keys) # パラメータ
mean_scores = bo.space.target # 評価指標
# 散布図プロット
sc = plt.scatter(df_history['gamma'].values, df_history['C'].values, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(bayes_params['gamma'][0], bayes_params['gamma'][1]) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(bayes_params['C'][0], bayes_params['C'][1]) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('gamma') # X軸ラベル
plt.ylabel('C') # Y軸ラベル
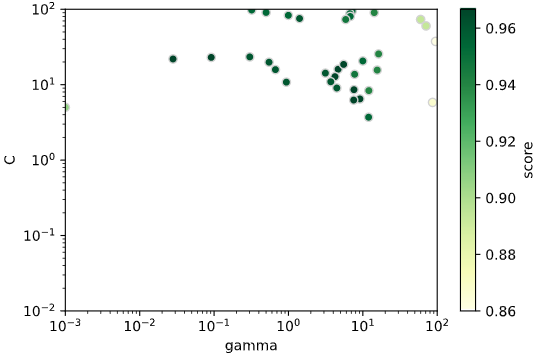
gamma, C共にLogスケールのパラメータなので、そのままチューニングすると範囲内の値が小さい側の探索がほとんど行われず、偏った探索となっていることがわかります。
そこで、Logスケールのパラメータは対数化してから指標算出メソッドに渡すよう修正します
from bayes_opt import BayesianOptimization
# パラメータ範囲(Tupleで範囲選択)
bayes_params = {'gamma': (0.001, 100),
'C': (0.01, 100)}
# パラメータ範囲を対数化
bayes_params_log = {k: (np.log10(v[0]), np.log10(v[1])) for k, v in bayes_params.items()}
# ベイズ最適化時の評価指標算出メソッド
def bayes_evaluate(gamma, C):
# 最適化対象のパラメータ
params = {'gamma': np.power(10 ,gamma),
'C': np.power(10, C)}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params_log, random_state=seed)
bo.maximize(init_points=5, n_iter=30, acq='ei') # 初期点数5、探索点数30、獲得関数EIを指定
# 最適パラメータの表示と保持
best_params = {k: np.power(10, v) for k, v in bo.max['params'].items()}
best_score = bo.max['target']
print(f'最適パラメータ {best_params}\nスコア {best_score}')
※bo.maximizeの引数init_points, n_iter, acqは適宜変更してください
最適パラメータ {'C': 100.0, 'gamma': 0.006392686948998503}
スコア 0.9666666666666667
先ほどと同様に探索履歴を可視化してみます
# パラメータと評価指標をndarrayに格納
df_history = pd.DataFrame(np.power(10 ,bo.space.params), columns=bo.space.keys) # パラメータ
mean_scores = bo.space.target # 評価指標
# 散布図プロット
sc = plt.scatter(df_history['gamma'].values, df_history['C'].values, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(bayes_params['gamma'][0], bayes_params['gamma'][1]) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(bayes_params['C'][0], bayes_params['C'][1]) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('gamma') # X軸ラベル
plt.ylabel('C') # Y軸ラベル
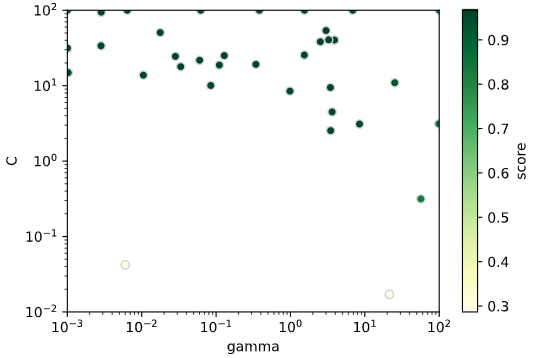
パラメータの値が小さい部分も探索されており、探索の偏りが改善されたことが分かります。
(Cが小さい部分の探索密度が低いですが、これは評価指標が悪いため獲得関数が小さくなることに由来します)
ベイズ最適化(Optuna)の場合
日本が誇るPreffered Networks社が開発した、ベイズ最適化ライブラリです。
BayesianOptimizationはガウス過程回帰 (BO-GP)を利用していますが、OptunaはTPEという手法を利用しており、より高速な最適化が実現できるようです。
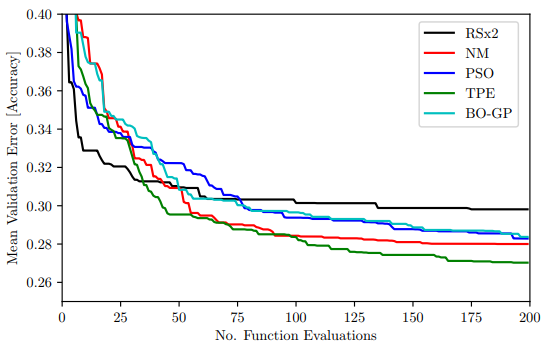
余談ですが、OptunaチートシートによるといつでもTPE > BO-GPというわけでもなく、パラメータ間に相関がある場合はBO-GPが推奨されるようです。機械学習のパラメータは基本的に独立に作られているはずなので、あまり関係ないかとは思いますが‥
ちなみに、日本発のライブラリですが日本語ドキュメントはありません(笑)
サンプルコードが充実しているので、こちらを見ながら実装するのが理解への近道になるかと思います(特にXGBoostやLGBMはパラメータ指定が複雑なので、いきなり自己流に入るとハマるかもしれません)
前置きが長くなりましたが、実装に移ります
import optuna
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
params = {
"gamma": trial.suggest_float("gamma", 0.001, 100, log=True),
"C": trial.suggest_float("C", 0.01, 100, log=True)
}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
study = optuna.create_study(direction="maximize",
sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=40)
# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'gamma': 0.0745934328572655, 'C': 63.512210106407046}
スコア 0.9666666666666667
BayesianOptimization同様、クロスバリデーションで評価指標算出するメソッドを定義する必要があります(後述のOptunaSearchCVという方法もあり)
他の探索法と同様、探索履歴を散布図で可視化してみます。
# パラメータと評価指標をndarrayに格納
param1_array = [trial.params['gamma'] for trial in study.trials] # パラメータgamma
param2_array = [trial.params['C'] for trial in study.trials] # パラメータC
mean_scores = [trial.value for trial in study.trials] # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(0.001, 100) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(0.001, 100) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('gamma') # X軸ラベル
plt.ylabel('C') # Y軸ラベル
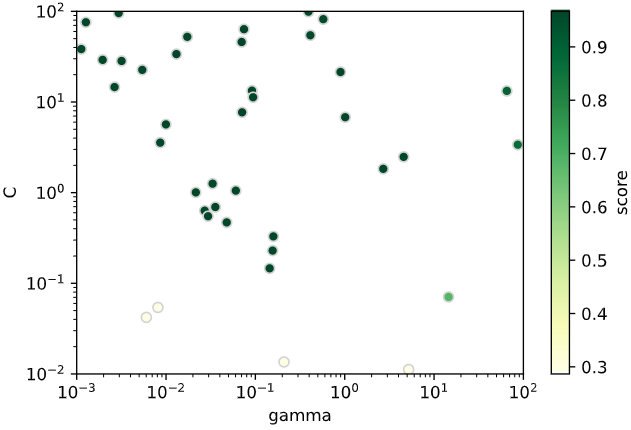
BayesianOptimizationとやや異なる探索位置ですが、評価指標の高い位置を集中的に探索するというベイズ最適化の特徴は、どちらも満たしているかと思います。
BayesianOptimizationと比べて便利だと感じたのが、パラメータの型やスケールを定義するAPIが含まれていることです。
前述のようにBayesianOptimizationでは対数スケールのパラメータを扱う際は、パラメータの対数を取る処理を別途実装する必要がありました。
一方でOptunaは、
trial.suggest_floatメソッドの引数に"log=True"を追加
するだけで、対数スケールのパラメータを探索することができます。
他にも、
・整数型のパラメータならtrial.suggest_intメソッドを使用
・文字列型(カテゴリカル)のパラメータならtrial.suggest_categoricalメソッドを使用
といった具合で、メソッドを変えるだけでパラメータの型の変化に対応してくれます
(実数型を扱うsuggest_floatとsuggest_uniformが紛らわしいですがこちらを見る限りどちらを使用しても良さそうです)
また、今回はクロスバリデーションはScikit-Learnで別途実装しましたが、クロスバリデーションも含め1メソッドで実装可能なOptunaSearchCVメソッドもあります。
GridSearchCVのように少ない行数で実装したい場合、こちらが便利かと思います。
このようにOptunaは、過去のライブラリの良いとこどりといった感じのAPIが多数準備されており、非常に使いやすいツールだと感じました。
手順5 学習・検証曲線の確認
学習、検証曲線で過学習の有無を確認します。
今回はOptunaで調整したパラメータ(gamma=0.0746, C=56.7)を例に描画してみます
学習曲線
学習曲線をプロットし、
・目的の性能を達成しているか
・過学習していないか
を確認します
from sklearn.model_selection import learning_curve
# 最適パラメータを学習器にセット
model.set_params(**best_params)
# 学習曲線の取得
train_sizes, train_scores, valid_scores = learning_curve(estimator=model,
X=X, y=y,
train_sizes=np.linspace(0.1, 1.0, 10),
cv=cv, scoring=scoring, n_jobs=-1)
# 学習データ指標の平均±標準偏差を計算
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# 検証データ指標の平均±標準偏差を計算
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(train_sizes, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(train_sizes, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(train_sizes, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(train_sizes, valid_high, valid_low, alpha=0.15, color='green')
# 最高スコアの表示
best_score = valid_center[len(valid_center) - 1]
plt.text(np.amax(train_sizes), valid_low[len(valid_low) - 1], f'best_score={best_score}',
color='black', verticalalignment='top', horizontalalignment='right')
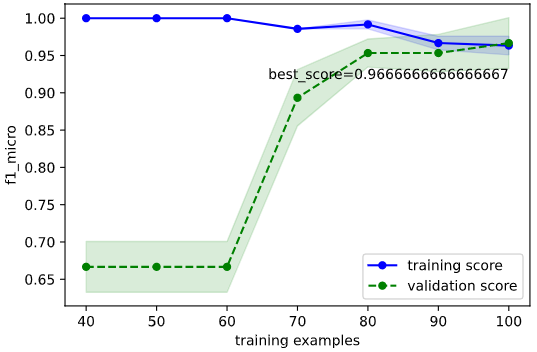
2.5の確認方法に基づいて確認すると、下記のようにOKと判断できます
・目的の性能を達成しているか → 目標性能は定めていないが、チューニング前より向上(0.96 → 0.967)したのでOKとする
・過学習していないか → 検証データ指標と学習データ指標が収束しているのでOK
検証曲線
検証曲線をプロットし、
・性能の最大値を捉えられているか
・過学習していないか
を確認します
# 検証曲線描画対象パラメータ
valid_curve_params = {'gamma': [0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100],
'C': [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]}
# 最適パラメータを上記描画対象に追加
for k, v in valid_curve_params.items():
if best_params[k] not in v:
v.append(best_params[k])
v.sort()
for i, (k, v) in enumerate(valid_curve_params.items()):
# モデルに最適パラメータを適用
model.set_params(**best_params)
# 検証曲線を描画
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# 最適パラメータを縦線表示
plt.axvline(x=best_params[k], color='gray')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale('log')
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
2.5の確認方法に基づいて確認すると、下記のようにOKと判断できます
・性能の最大値を捉えられているか → 頂点が広く分かりづらいが、gammaもCもだいたい捉えられていそうなのでOKとする
・過学習していないか → 最適パラメータにおいて学習データ指標と検証データ指標が近いのでOK
チューニング後のモデルを可視化
最後に、チューニング後のモデルを可視化します(チューニング前と比較)
classplot.class_separator_plot(model, ['petal_width', 'petal_length'], 'species', iris,
cv=cv, display_cv_indices=[0, 1, 2],
clf_params=best_params)
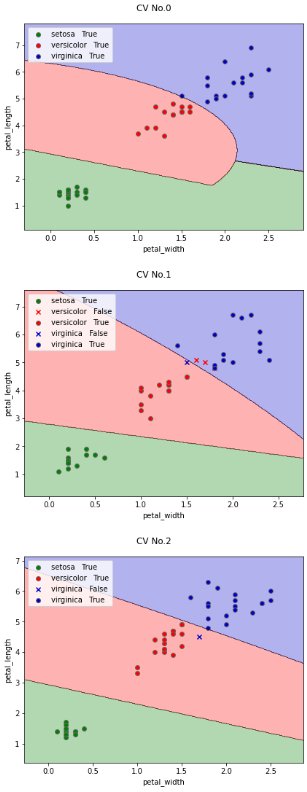
チューニング前から性能が良かったので、決定境界を見ても性能向上したかどうかは分かりませんが、
少なくとも判定を間違えた数は6個→5個に減っていることが分かります。
3.2 パイプライン処理(標準化+SVM)による分類
前例のirisデータセットでは、説明変数のスケールがcmで揃っていましたが、
現実のデータは変数のスケールが揃わない事が多いです。
SVMのような特徴量空間上での距離に基づくアルゴリズムでは、
変数のスケールが揃っていないと特定の変数が過大評価され、性能が落ちてしまいます。
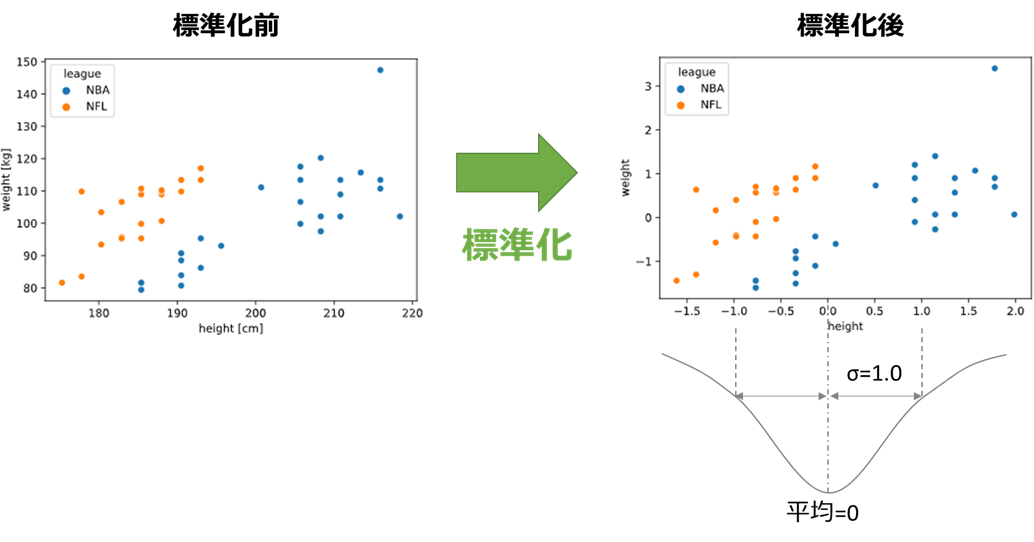
そのため、変数のスケールを揃えて性能向上させるための前処理として、標準化が必要となります。
標準化とは平均が0、標準偏差が±1となるよう説明変数をスケール変換することです。
あるデータxの平均をμ、標準偏差をσとすると、xを標準化したx'は
x'=\frac{x-\mu}{\sigma}
標準化のような前処理を含めたチューニングを行う場合、パイプラインを利用する必要があります。
パイプラインに関しては別記事で詳説しているので、本記事では詳細に触れず、実装を進めていきます。
データセットには、こちらの記事のNFL選手とNBA選手の分類を利用します。
チューニング前のモデルの確認
データセットを読み込み、"height"(身長), "weight"(体重)を特徴量として可視化します
import pandas as pd
import seaborn as sns
df_athelete = pd.read_csv(f'./sample_data/nba_nfl_2.csv')
sns.scatterplot(x='height', y='weight', data=df_athelete, hue='league') # 説明変数と目的変数のデータ点の散布図をプロット
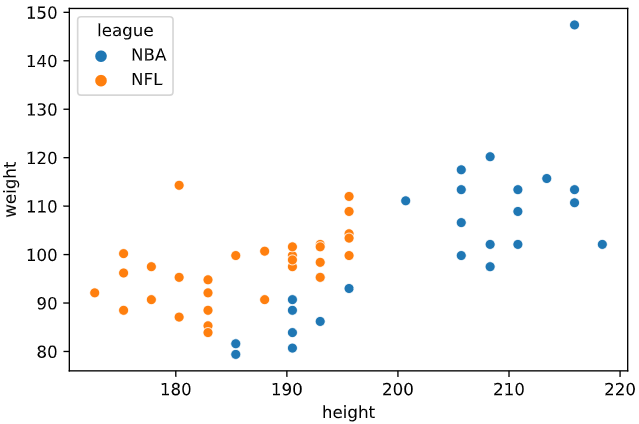
3.1と同様に、3分割クロスバリデーションでチューニング前(デフォルトパラメータ)のモデルを可視化します。
なお、3.1のときとの実装の違いは、
・前処理に標準化(StandardScaler)を加えるため、Pipelineクラスでパイプライン化
・N数が40(1クラスあたり20)と少ないため、クロスバリデーションにStratified K-Foldを使用
・評価指標neg_log_lossの確率計算のために、SVCの引数"probability=True"を指定
となります。
また、"probability=True"を指定する確率計算に乱数シードを利用するため、結果の再現性を取るためにSVCの引数"random_state"を指定します。
from seaborn_analyzer import classplot
from sklearn.svm import SVC
from sklearn.model_selection import StratifiedKFold
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 乱数シード
seed = 42
# モデル作成(標準化+SVMパイプライン、loglossを使うためprobability&random_state指定が必要)
model = Pipeline([("scaler", StandardScaler()), ("svm", SVC(probability=True, random_state=seed))])
# クロスバリデーションして決定境界を可視化
cv = StratifiedKFold(n_splits=3, shuffle=True, random_state=seed) # StratifiedKFoldでクロスバリデーション分割指定
classplot.class_separator_plot(model, ['height', 'weight'], 'league', df_athelete,
cv=cv, display_cv_indices=[0, 1, 2])
こちらもデフォルトでもいい感じで分類できていそうですね‥(笑)
ひとまずチューニングを続けていきます。
手順1 最大化したい評価指標の定義
今回は
・2クラス分類
・不均衡データではない
ので、2.1のフローに基づき"logloss"を採用します。
チューニング前の評価指標をクロスバリデーションで算出します。
from sklearn.model_selection import cross_val_score
import numpy as np
X = df_athelete[['height', 'weight']].values # 説明変数をndarray化
y = df_athelete['league'] # 目的変数をndarray化
scoring = 'neg_log_loss' # 評価指標をneg_log_lossに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
scores=[-0.17737566 -0.1880831 -0.21874771]
average_score=-0.1947354941390147
このクロスバリデーションで求めたスコアの平均値average_scoreが、パラメータチューニングで向上させたい指標となります。
また、パラメータgammaはこちらのgamma='scale'のときの式で動的に計算されるので、
参考値として計算しておきます。
print(f'gamma = {1 /(X.shape[1] * StandardScaler().fit_transform(X).var())}')
gamma = 0.5000000000000001
今回のデータではデフォルトのgamma≒0.5であることがわかります
手順2 パラメータ種類と範囲の選択
・種類
SVMにはgammaとCの2種類のパラメータしか存在しないので、どちらもチューニング対象として採用します。
・範囲
適当な初期範囲を定めて検証曲線をプロットし、その結果に基づいて範囲を調整していきます。
なお、今回のようにPipelineクラスでパイプラインを構成している場合、パラメータ名を
"[学習器名]__[パラメータ名]"
とする必要があります(例:"svm"のパラメータ"C"をチューニングしたい場合、"svm__C"とする)
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
cv_params = {'svm__gamma': [0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 100, 1000],
'svm__C': [0.001, 0.01, 0.1, 0.3, 1, 3, 10, 100, 1000]}
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale('log')
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
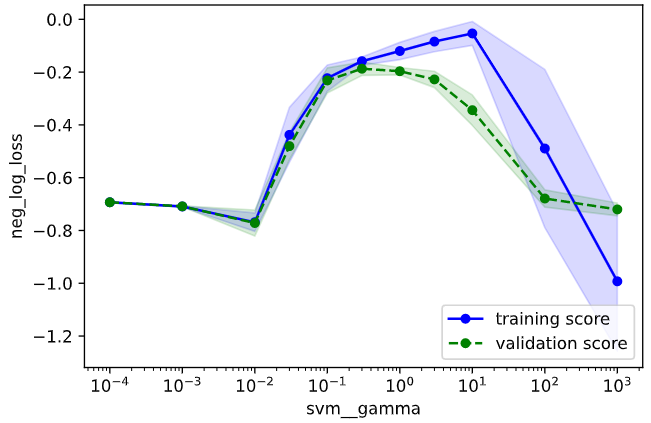
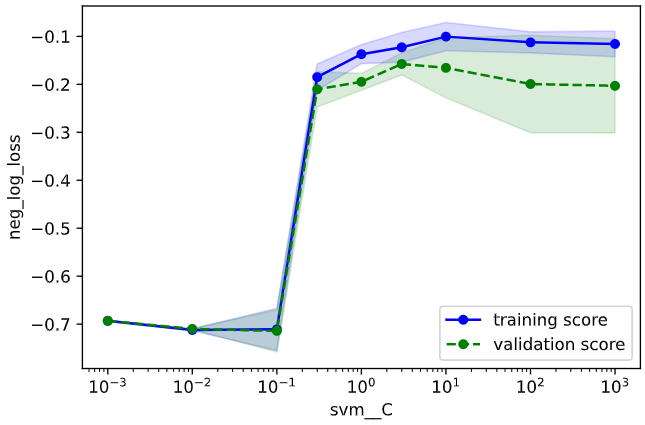
plt.show()
3.1の教訓から広めに範囲を取った事が功を奏したのか、どちらのパラメータも過学習、未学習の傾向がつかめている事が分かります。
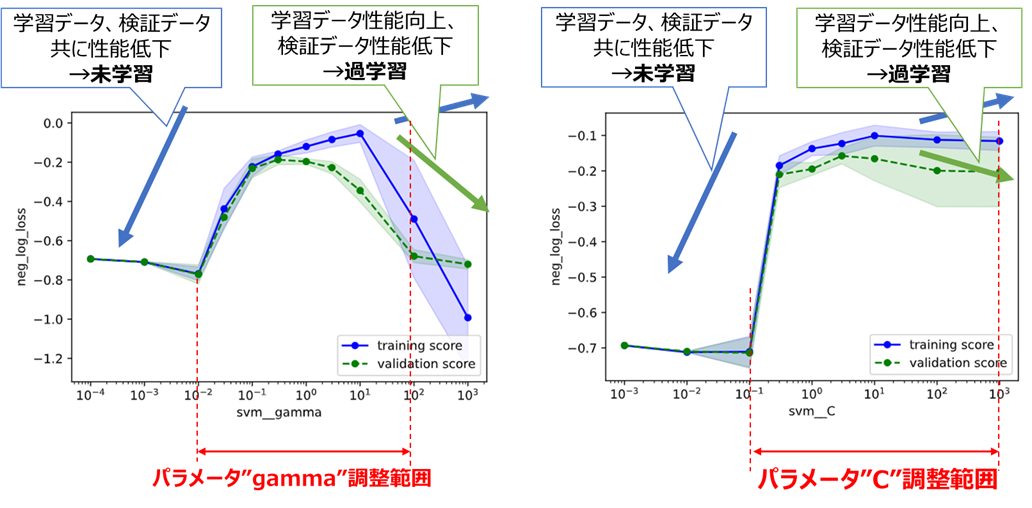
今回も未学習・過学習の小さい範囲よりも少し広めにとって、
パラメータ"gamma":0.01~100
パラメータ"C":0.1~1000
を調整範囲とすることとします。
手順3&4 パラメータ選択&クロスバリデーション
3.1のときと同様に、下記A、B、C (BayesianOptimization)、C (Optuna)の4種類の実装法をそれぞれ解説します。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | **グリッドサーチ ** | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
グリッドサーチの場合
GridSearchCVクラスで、グリッドサーチによる最適化を実行します
from sklearn.model_selection import GridSearchCV
# 最終的なパラメータ範囲
cv_params = {'svm__gamma': [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100],
'svm__C': [0.1, 0.3, 1, 3, 10, 30, 100, 300, 1000]}
# グリッドサーチのインスタンス作成
gridcv = GridSearchCV(model, cv_params, cv=cv,
scoring=scoring, n_jobs=-1)
# グリッドサーチ実行(学習実行)
gridcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = gridcv.best_params_
best_score = gridcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'svm__C': 10, 'svm__gamma': 0.3}
スコア -0.17112358617348056
C=10, gamma=0.3のときに評価指標loglossが最大となり、その時の値は-0.171‥であることが分かります
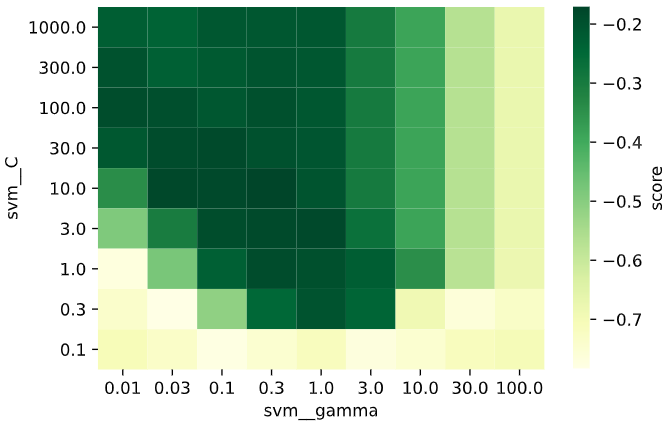
グリッドサーチで選択したパラメータと、算出した評価指標との関係をヒートマップで表示します。
import pandas as pd
# パラメータと評価指標をデータフレームに格納
param1_array = gridcv.cv_results_['param_svm__gamma'].data.astype(np.float64) # パラメータgamma
param2_array = gridcv.cv_results_['param_svm__C'].data.astype(np.float64) # パラメータC
mean_scores = gridcv.cv_results_['mean_test_score'] # 評価指標
df_heat = pd.DataFrame(np.vstack([param1_array, param2_array, mean_scores]).T,
columns=['svm__gamma', 'svm__C', 'test_score'])
# グリッドデータをピボット化
df_pivot = pd.pivot_table(data=df_heat, values='test_score',
columns='svm__gamma', index='svm__C', aggfunc=np.mean)
# 上下軸を反転(元々は上方向が小となっているため)
df_pivot = df_pivot.iloc[::-1]
# ヒートマップをプロット
sns.heatmap(df_pivot, cmap='YlGn', cbar_kws={'label': 'score'})
ランダムサーチの場合
RondomizedSearchCVクラスで、ランダムサーチによる最適化を実行します
from sklearn.model_selection import RandomizedSearchCV
# パラメータの密度をグリッドサーチのときより増やす
cv_params = {'svm__gamma': [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100],
'svm__C': [0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000]}
# ランダムサーチのインスタンス作成
randcv = RandomizedSearchCV(model, cv_params, cv=cv,
scoring=scoring, random_state=seed,
n_iter=50, n_jobs=-1)
# ランダムサーチ実行(学習実行)
randcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = randcv.best_params_
best_score = randcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'svm__gamma': 0.2, 'svm__C': 10}
スコア -0.17418521473927107
C=10, gamma=0.2のときに評価指標loglossが最大となり、その時の値は-0.174(グリッドサーチのときより少し悪い)であることが分かります
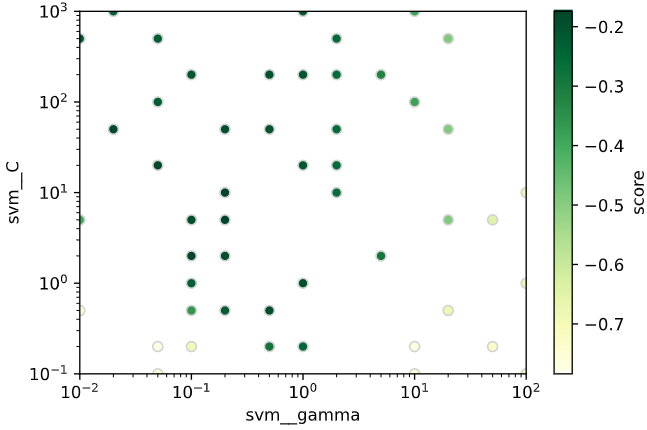
ランダムサーチで選択したパラメータと、算出した評価指標との関係を散布図で表示します。
# パラメータと評価指標をndarrayに格納
param1_array = randcv.cv_results_['param_svm__gamma'].data.astype(np.float64) # パラメータgamma
param2_array = randcv.cv_results_['param_svm__C'].data.astype(np.float64) # パラメータC
mean_scores = randcv.cv_results_['mean_test_score'] # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(np.amin(cv_params['svm__gamma']), np.amax(cv_params['svm__gamma'])) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(np.amin(cv_params['svm__C']), np.amax(cv_params['svm__C'])) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('svm__gamma') # X軸ラベル
plt.ylabel('svm__C') # Y軸ラベル
ベイズ最適化(BayesianOptimization)の場合
BayesianOptimizationによるベイズ最適化の実装法を解説します。
3.1の教訓に基づき、今回は最初から対数スケールに対応した実装法を採用します
from bayes_opt import BayesianOptimization
# パラメータ範囲(Tupleで範囲選択)
bayes_params = {'svm__gamma': (0.01, 100),
'svm__C': (0.1, 1000)}
# パラメータ範囲を対数化
bayes_params_log = {k: (np.log10(v[0]), np.log10(v[1])) for k, v in bayes_params.items()}
# ベイズ最適化時の評価指標算出メソッド
def bayes_evaluate(svm__gamma, svm__C):
# 最適化対象のパラメータ
params = {'svm__gamma': np.power(10 ,svm__gamma),
'svm__C': np.power(10, svm__C)}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params_log, random_state=seed)
bo.maximize(init_points=5, n_iter=40, acq='ei')
# 最適パラメータの表示と保持
best_params = {k: np.power(10, v) for k, v in bo.max['params'].items()}
best_score = bo.max['target']
print(f'最適パラメータ {best_params}\nスコア {best_score}')
※bo.maximizeの引数init_points, n_iter, acqは適宜変更してください
最適パラメータ {'svm__C': 3.7411698145492176, 'svm__gamma': 0.512102940492465}
スコア -0.15602935692141787
グリッドサーチ、ランダムサーチよりもスコアが改善していることが分かります。
探索履歴を可視化してみます
# パラメータと評価指標をndarrayに格納
df_history = pd.DataFrame(np.power(10 ,bo.space.params), columns=bo.space.keys) # パラメータ
mean_scores = bo.space.target # 評価指標
# 散布図プロット
sc = plt.scatter(df_history['svm__gamma'].values, df_history['svm__C'].values, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(bayes_params['svm__gamma'][0], bayes_params['svm__gamma'][1]) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(bayes_params['svm__C'][0], bayes_params['svm__C'][1]) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('svm__gamma') # X軸ラベル
plt.ylabel('svm__C') # Y軸ラベル
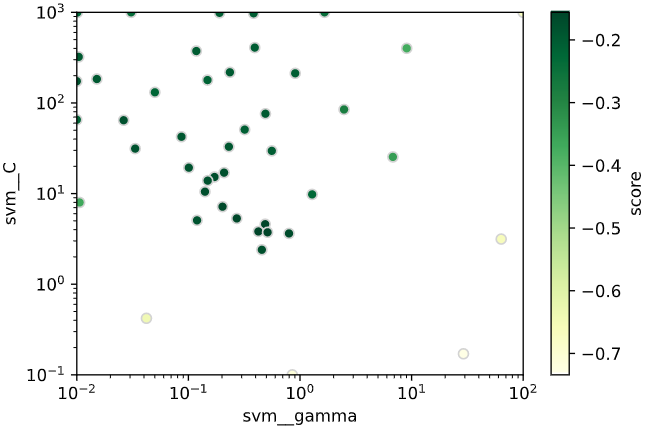
スコアが高い部分を集中探索しており、ベイズ最適化による効率探索が実現できていることが分かります。
ベイズ最適化(Optuna)の場合
Optunaによるベイズ最適化の実装法を解説します。
import optuna
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
params = {
"svm__gamma": trial.suggest_float("svm__gamma", 0.01, 100, log=True),
"svm__C": trial.suggest_float("svm__C", 0.1, 1000, log=True)
}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
study = optuna.create_study(direction="maximize",
sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=40)
# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
最適パラメータ {'svm__gamma': 0.6504753435540145, 'svm__C': 2.709993949798205}
スコア -0.1603081455942764
他の探索法と同様、探索履歴を散布図で可視化してみます。
# %% Optunaの評価指標を可視化(散布図)
# パラメータと評価指標をndarrayに格納
param1_array = [trial.params['svm__gamma'] for trial in study.trials] # パラメータgamma
param2_array = [trial.params['svm__C'] for trial in study.trials] # パラメータC
mean_scores = [trial.value for trial in study.trials] # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc) # カラーバー追加
cbar.set_label('score') # カラーバーのタイトル
plt.xscale('log') # 第1軸をlogスケールに
plt.yscale('log') # 第2軸をlogスケールに
plt.xlim(0.01, 100) # X軸表示範囲をデータ最小値~最大値に
plt.ylim(0.01, 1000) # Y軸表示範囲をデータ最小値~最大値に
plt.xlabel('svm__gamma') # X軸ラベル
plt.ylabel('svm__C') # Y軸ラベル
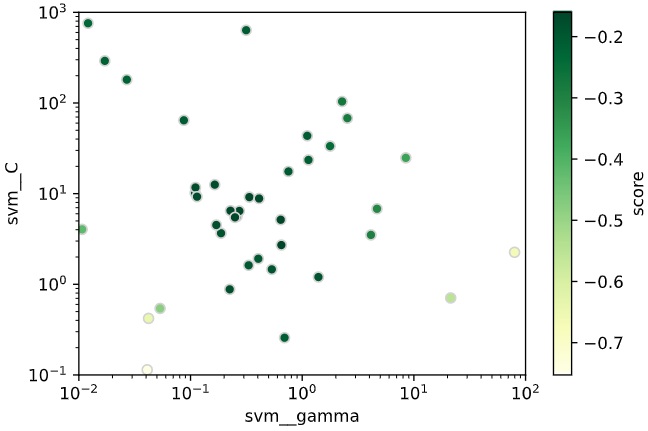
BayesianOptimizationと同様、スコアが高い部分を集中探索しており、ベイズ最適化による効率探索が実現できていることが分かります。
グリッドサーチ、ランダムサーチ、ベイズ最適化、いずれの手法でもパイプラインだからといって特別な実装はほぼ必要なく(パラメータ名に学習器名を追加するくらいでしょうか)、**パイプラインの効果を実感**できたかと思います!
手順5 学習・検証曲線の確認
学習、検証曲線で過学習の有無を確認します。
今回はOptunaで調整したパラメータ(gamma=0.546‥, C=9.32‥)を例に描画してみます
学習曲線
学習曲線をプロットし、
・目的の性能を達成しているか
・過学習していないか
を確認します
from sklearn.model_selection import learning_curve
# 最適パラメータを学習器にセット
model.set_params(**best_params)
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1)
print(scores.mean())
# 学習曲線の取得
train_sizes, train_scores, valid_scores = learning_curve(estimator=model,
X=X, y=y,
train_sizes=np.linspace(0.1, 1.0, 10),
cv=cv, scoring=scoring, n_jobs=-1)
# 学習データ指標の平均±標準偏差を計算
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# 検証データ指標の平均±標準偏差を計算
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(train_sizes, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(train_sizes, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(train_sizes, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(train_sizes, valid_high, valid_low, alpha=0.15, color='green')
# 最高スコアの表示
best_score = valid_center[len(valid_center) - 1]
plt.text(np.amax(train_sizes), valid_low[len(valid_low) - 1], f'best_score={best_score}',
color='black', verticalalignment='top', horizontalalignment='right')
# 軸ラベルおよび凡例の指定
plt.xlabel('training examples') # 学習サンプル数を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
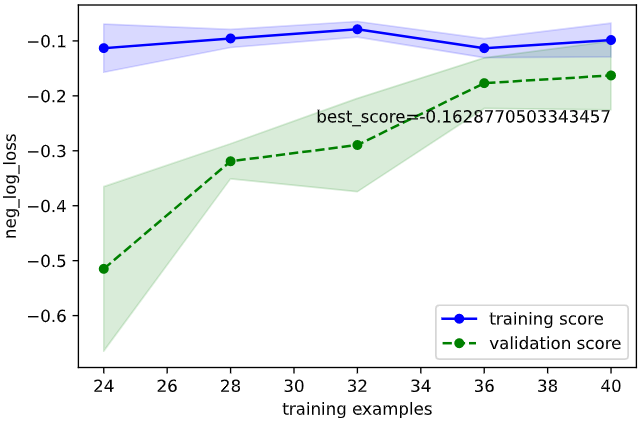
2.5の確認方法に基づいて確認すると、下記のようにOKと判断できます
・目的の性能を達成しているか → 目標性能は定めていないが、チューニング前より向上(-0.194 → -0.162)したのでOKとする
・過学習していないか → 検証データ指標と学習データ指標が収束しているのでOK
検証曲線
検証曲線をプロットし、
・性能の最大値を捉えられているか
・過学習していないか
を確認します
# 検証曲線描画対象パラメータ
valid_curve_params = {'svm__gamma': [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100],
'svm__C': [0.1, 0.3, 1, 3, 10, 30, 100, 300, 1000]}
# 最適パラメータを上記描画対象に追加
for k, v in valid_curve_params.items():
if best_params[k] not in v:
v.append(best_params[k])
v.sort()
for i, (k, v) in enumerate(valid_curve_params.items()):
# モデルに最適パラメータを適用
model.set_params(**best_params)
# 検証曲線を描画
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# 最適パラメータを縦線表示
plt.axvline(x=best_params[k], color='gray')
best_index = np.where(np.array(v)==best_params[k])
best_score = valid_center[best_index][0]
plt.text(best_params[k], np.amax(valid_center), f'best_{k}={best_params[k]}\nbest_score={best_score}',
color='black', verticalalignment='bottom', horizontalalignment='left')
# スケールを'log'に(線形なパラメータは'linear'にするので注意)
plt.xscale('log')
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
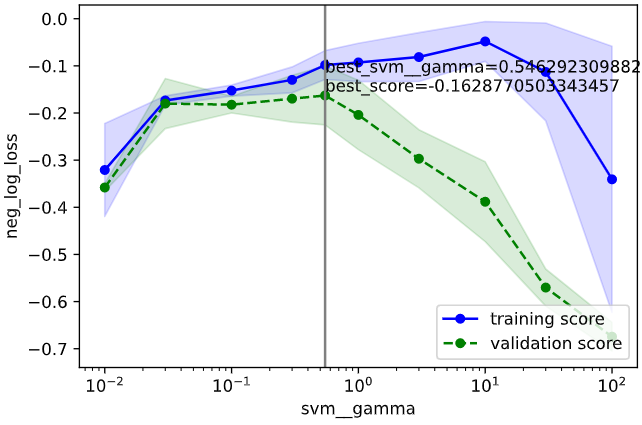
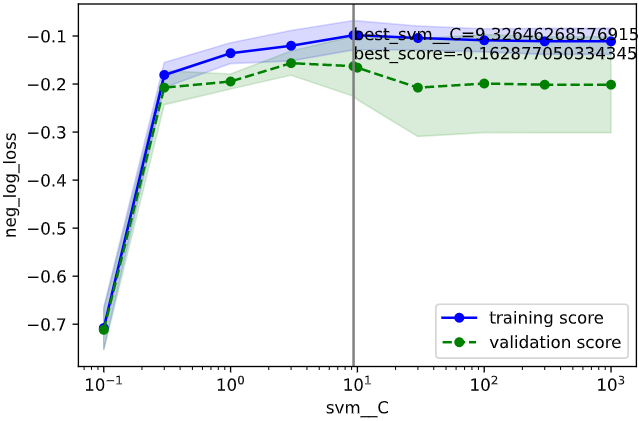
2.5の確認方法に基づいて確認すると、下記のようにOKと判断できます
・性能の最大値を捉えられているか → gammaもCもだいたい捉えられていそうなのでOKとする
・過学習していないか → 最適パラメータにおいて学習データ指標と検証データ指標が近いのでOK
チューニング後のモデルを可視化
最後に、チューニング後のモデルを可視化します(チューニング前と比較)
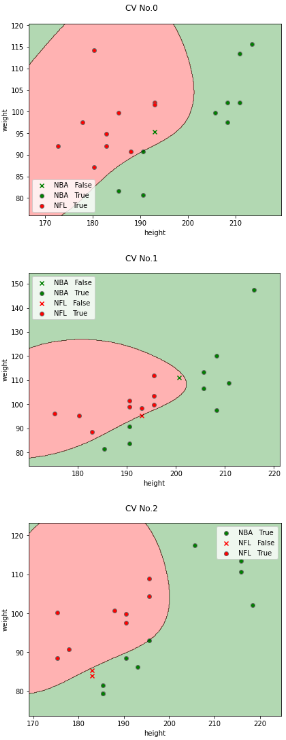
classplot.class_separator_plot(model, ['height', 'weight'], 'league', df_athelete,
cv=cv, display_cv_indices=[0, 1, 2],
model_params=best_params)
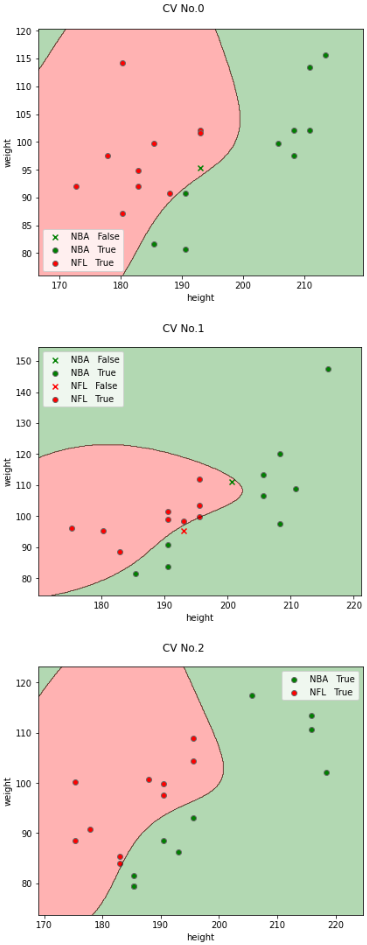
チューニング前から性能が良かったので、決定境界を見ても性能向上したかどうかは分かりませんが、
少なくとも判定を間違えた数は5個→3個に減っていることが分かります。
その他諸注意
下記を押さえておくと、より効率的なパラメータチューニングができるかと思います。
評価指標選択(本文2-1)時の注意
「2-1 評価指標選択」実施時には、下記の知識があると助けとなります。
分類指標、回帰指標に分けて解説します
分類指標
注意点1 不均衡データ
各クラスのデータ数の偏りが大きい「不均衡データ」(例:10000人の非がん患者と、10人のがん患者とを分類する問題)では、Accuracy等の指標を使用するのは適切ではありません。
詳細説明はこちらが分かりやすいので割愛しますが、
不均衡データにおいては、PR-AUCやF1-scoreが適切な指標となります
注意点2:LogLossと正負
LogLossは小さいほど良い指標なので、他の指標では「最大化」するようチューニングするのに対し、これらの指標は「最小化」するようチューニングする必要があります。
ただし、scikit-learnではLogLossにマイナス1を掛けたneg_log_lossという指標が指定できるので、これらの指標を使用すれば通常通り「最大化」するようチューニングすることができ、実用上は他の指標との違いを意識する必要はありません
注意点3 多クラス分類におけるF1-score
3種類以上の多クラス分類(例:リンゴ、ミカン、ブドウを分類)の場合、Scikit-LearnにおいてF1-scoreの算出法にはf1_micro, f1_macro, f1_weightの3種類があります。
| scikit-learnでの名称 | 手法 | 不均衡データへの強さ |
|---|---|---|
| 'f1_micro' | 全体のTP,FN.FP,TNを和にしてからF値を計算 | 弱い |
| 'f1_macro' | クラスごとにF値を計算して平均 | バランス |
| 'f1_weighted' | クラスごとにF値を計算してデータ数で加重平均 | 強い |
| 詳細はこちらやこちらが詳しいですが、不均衡データにおいては、小さいクラスの影響を大きく評価するf1_macroの方がf1_microより良いと言われています。 | ||
| (逆に、大きなクラスさえ正解していれば小さいクラスでの性能は問わない、という場合はf1_microを選択するのも可です) |
f1_weightedは加重平均する分f1_macroよりもさらに不均衡データへの対応力を強化していますが、逆に小さいクラスが大きく評価されすぎる可能性もあるので、どちらを採用するかは実際のデータを見て決めるのが良いかと思います。
(といってもいきなり選択するのは難しいので、実用的には両方でチューニングし、思うように分類できていた方を採用する、という形で良いかと思います)
注意点4 多クラス分類におけるAUC
F1-Scoreと同様、AUCにおいても他クラス分類では複数の手法が存在し、
Scikit-Learnにおいては以下の4種類が指定可能です。
4種類の手法は、内部的にはAUC算出用のroc_auc_scoreメソッドにおいて、'average'引数、'multi_class'引数を変えています。
| scikit-learnでの名称 | 'average'引数 | 'multi_class'引数 |
|---|---|---|
| 'roc_auc_ovr' | 'ovr' | 'macro' |
| 'roc_auc_ovo' | 'ovo' | 'macro' |
| 'roc_auc_ovr_weighted' | 'ovr' | 'weighted' |
| 'roc_auc_ovo_weighted' | 'ovo' | 'weighted' |
| 'average'引数はF1における'macro'と'weighted'と同様の考え方です(なぜか'micro'はないようです) |
'multi_class'引数は、AUCを算出するときに、
ovr:「算出対象クラス vs 他のクラスをまとめて1クラス」として算出
ovo:「算出対象クラス vs 他のクラス」を1つずつ別個に算出し、最後に平均を取る
(指標算出ではなく学習なので厳密には異なりますが、こちらが参考になるかと思います)
不均衡データに対する対応力としては、前述のroc_auc_scoreメソッド公式を見る限り、
ovo > ovr
weight > macro
となります。
ただしF1-Scoreのときと同様、対応力を上げすぎると逆に小さなクラスが過大評価される恐れもありますし、一番対応力の弱そうな'roc_auc_ovr'でも、不均衡データに対する一応の対応はしている(avarage='micro'ではない)ので、こちらもバランスを見て決めるのが良いかと思います。
回帰指標
注意点1:R2と相関係数
良くある誤解ですが、scikit-learnにおけるR2(決定係数)は、相関係数(ピアソンの相関係数)の2乗とは異なります。
近い値にはなるので混同していても気づかない(実害が出ない)ことが多いですが、厳密には異なることをご留意ください
注意点2:RMSE・RMSLEと正負
RMSEおよびRMSLEは小さいほど良い指標なので、他の指標では「最大化」するようチューニングするのに対し、これらの指標は「最小化」するようチューニングする必要があります。
ただし、scikit-learnではRMSEにマイナス1を掛けたneg_root_mean_squared_errorや、RMSLEの2乗にマイナス1を掛けたneg_mean_squared_log_errorという指標が指定できるので、これらの指標を使用すれば通常通り「最大化」するようチューニングすることができ、実用上は他の指標との違いを意識する必要はありません
注意点3:RMSEとRMSLEの使い分け
RMSLEの特徴として、対数正規分布を前提としている事(RMSEは正規分布)や、推定値のマイナス側誤差がプラス側誤差よりも大きく評価される事が挙げられます。
これらの特徴に基づき、
・値の範囲が大きい場合(例:目的変数が正規分布よりも対数正規分布に近いロングテールな分布のとき)
・推定値が実測値より小さいときのペナルティを大きく評価したい場合(例:在庫切れしたくない需要予測)
場合に、RMSEよりRMSLEが使用されることが多いです
注意点4:勾配ブースティング系アルゴリズムとR2-score
別記事作成予定ですが、XGBoostやLGBM等の勾配ブースティング系アルゴリズムでは、探索初期段階でのR2の値が1を大きく超える(予測値が全て等しくなったときに発生)外れ値となることが多く、この外れ値に引きずられてパラメータチューニングの効率が著しく悪化するようです。
ですので、
勾配ブースティング系アルゴリズムのチューニング指標はRMSEやRMSLEを使用するのが良さそうです
最終性能評価
前述したパラメータチューニングの手法では、過学習を防ぐために学習データとテストデータを分け、
さらにクロスバリデーションで平均を取る、という方法をとっています。
これにより過学習の影響を防ぎ、未知データに対して推定性能を上げるようチューニングできるのですが、
特にデータ数が少ない時などは、クロスバリデーションで分割された学習データの偏りに左右され、**多少の過学習(クロスバリデーションのデータの分け方に過剰適合した状態)**が発生してしまいます
この「クロスバリデーション分割に対する過学習」の影響も含めた性能を評価するため、
パラメータチューニング用のデータとは別にテストデータをあらかじめ分割しておき、
チューニング後にこの最終評価用テストデータで最終的な性能評価を実施する場合も多いです。
実際のフローとしては、下図のようにチューニングのフローの前後にデータ分割と最終性能評価を加える形が一般的です
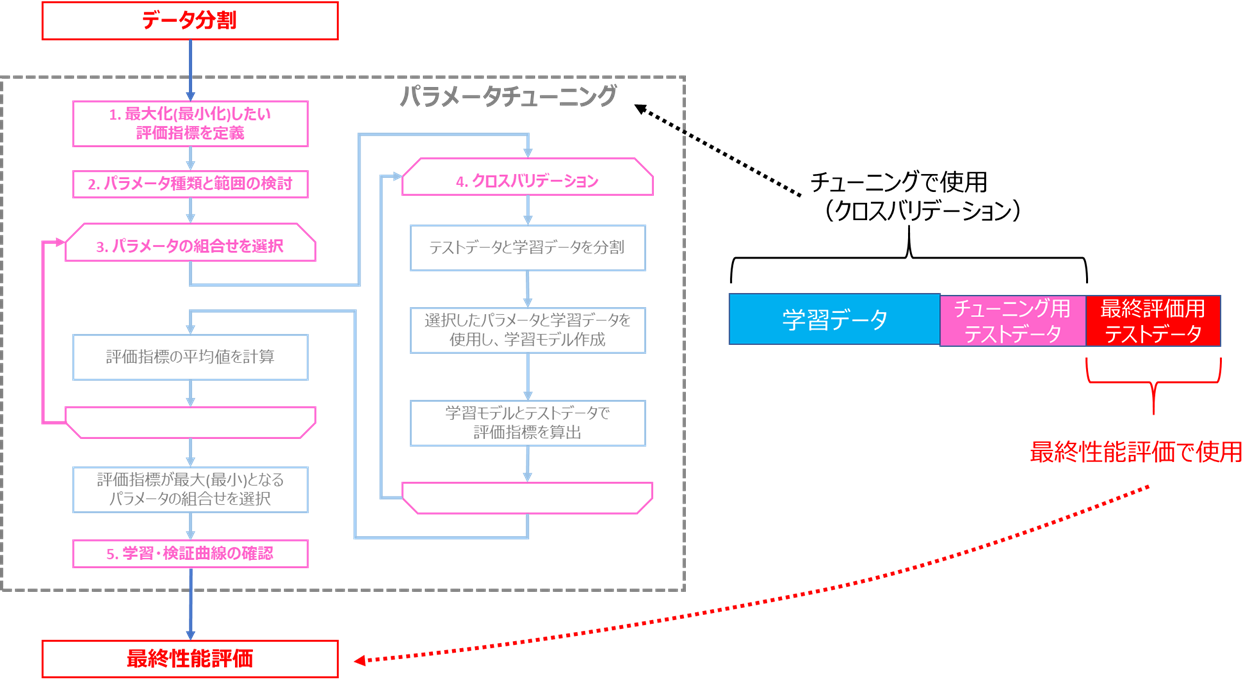
この方法では、2種類の「テストデータ」が登場するので、
・パラメータチューニング用のテストデータ(「検証データ」とも言う)
・最終性能評価用のテストデータ(狭義の「テストデータ」)
と分けて考える必要があります。
チューニングしなくてもいい感じで学習してくれるアルゴリズム
ここまで読まれた方の中には
「チューニングって必要知識も実装量も多くて面倒くさい!」
という感想を持った方も多いかと思います。
そんな方に朗報ですが、
分類:ランダムフォレスト
回帰:ガウス過程回帰
は、チューニングなしでも割といい感じで学習してくれる傾向があると感じたので(ネットを探しても同じ意見がいくつか見つかりました)、簡易に開発できるかと思います。
ただし、どちらのアルゴリズムも学習データの密度が低い部分の推定は不正確になりがちなので、未知データへの対応力を重視する方はSVMやXGBoostなどチューニングが効果を発揮するアルゴリズムでチューニングを実施する事をお勧めします。
機械学習における「パラメータ」
ここまで読み進めた方は理解されているかと思いますが、機械学習において「パラメータ」と呼べる存在は多数存在し、
下記の3種類がよく登場するかと思います
・学習で決定するパラメータ(例:線形回帰における直線の傾き)
・ハイパーパラメータ(これが狭義の「パラメータ」、例:SVMのGammaやC)
・パラメータチューニングで使用する設定値(例:ベイズ最適化やランダムサーチのn_iterなど)
混同しないよう注意しましょう!
参考書籍
・O'Reilly Japan - Pythonではじめる機械学習
・impress top gear - Python機械学習プログラミング 達人データサイエンティストによる理論と実践