はじめに
機械学習の定番アルゴリズムの1つである「サポートベクターマシン(SVM)」ですが、
実用的、かつ比較的シンプルなアルゴリズムから、入門書等でも取り上げられることが多いです。
ただし、解説の抜け漏れや、難解すぎる書籍や記事が多いと感じたので、備忘録も兼ねて
・網羅的
・平易な説明
・実データでの実装例あり(Pythonのライブラリscikit-learn(インストール法)を使用)
を心がけ、高校生でも「理解した!」と言えるような記事を目指したいと思います。
注意
注意1
・高校生でもわかると銘打ってしまったのに申し訳ありませんが、
高校で勉強しない(理系の大学1~2年で学習)偏微分の知識が出てきます。
大変分かりやすいYouTube動画があるので、こちらを見れば「理解した!」と言えるのではと思います。
偏微分
ラグランジュの未定乗数法
不等式条件のラグランジュの未定乗数法(KKT条件)
注意2
・本文中の数式に
$${W^T}X$$
のように"T"という記号が出てきますが、これは行列の縦横を交換する「転置」です。
一見難解に見えますが、ベクトルの内積を行列の積で表現するための慣用的な表現で、
上式の場合ベクトルWとXの内積と読み替えれば問題ありません。
注意3
・アルゴリズムの最後に出てくる2次計画問題に関しては、私もソルバー頼みで解法を理解しているわけではないので、説明を省略することをご了承いただければと思います。
注意4
サンプルコードを動かすためには、以下のライブラリをインストールしてください
(カッコ内は私の環境でのバージョン、Pythonは3.9.4を使用)
seaborn (0.11.1)
numpy (1.20.1)
pandas (1.2.2)
matplotlib (3.3.4)
scipy (1.6.0)
scikit-learn (0.24.1)
mlxtend (0.18.0)
機械学習におけるサポートベクターマシンの位置づけ
サポートベクターマシンは、主に「分類」に使用されるアルゴリズムとなります。
・分類の例
ケース1:体温、せきの回数から、病気の有無を推定する
ケース2:長さ、重さ、色から果物の種類(リンゴ、ミカン、ブドウ)を推定する
ケース1は「有り」か「無し」の2種類の分類しか存在しないので、2値分類と呼び、
ケース2は3種類以上の分類が存在するので、多値分類(多クラス分類)と呼びます
多値分類とサポートベクターマシン
本記事では2値分類のアルゴリズムを解説していますが、2値分類のアルゴリズムを複数並べることで、他値分類にも対応できます。
詳細はこちらが参考になります
回帰とサポートベクターマシン
本手法を回帰に応用した「サポートベクター回帰」と呼ばれる手法もありますが、分類と比べると利用頻度が低いため、本記事では割愛します。
サポートベクターマシンの基本概念
例えば下図のような2つの説明変数(例:体温、せきの回数)を使って、
クラス1(例:病気あり)とクラス2(例:病気なし)を分類したいとします。

機械学習の分類問題においては、これらのクラス間に境目となる直線や曲線(3次元以上では面)を引くことで、分類を実現します。
この境目となる直線や曲線を、決定境界と言います。
上の例において直線で決定境界を引いた場合を考えます。
下図の決定境界Aと決定境界Bではどちらが分類性能が高く見えるでしょうか?

多くの人が、決定境界Aの方が高性能だと感じるかと思います。
そして決定境界Bが良くないと思う根拠として、
「赤く塗りつぶした点までの距離が近すぎて、誤判定しそう」
が、感覚的に違和感のない説明になるかと思います。
「最も近い点(サポートベクター)までの距離が遠くなるよう決定境界を決める」分類手法を、
サポートベクターマシンと呼びます。
例えば、2次元において直線の方程式は
ax + by + c = 0
となります。
このとき、点(xi, yi)と直線の距離は
\frac{|ax_i+by_i+c|}{\sqrt{a^2+b^2}}
となるので、全ての学習データ(i=1,2,‥n)に対して
min_{i=1,2‥n}\frac{|ax_i+by_i+c|}{\sqrt{a^2+b^2}}
を最大化するa, bの組合せを探す(cは規格化して消去される)ことが、2次元におけるサポートベクターマシンの学習となります。
アルゴリズム詳細は次節で解説するので、まずは実データで実装してみましょう!
バスケットボール(NBA)選手とアメリカンフットボール(NFL)選手を身長体重で識別できるかを試してみます
name,league,position,height,weight
Wilt Chambelain,NBA,C,215.9,113.4
Bill Russel,NBA,C,208.3,97.5
Kareem Abdul-Jabbar,NBA,C,218.4,102.1
Elvin Hayes,NBA,PF,205.7,106.6
Moses Malone,NBA,C,208.3,97.5
Tim Duncan,NBA,PF,210.8,113.4
Karl Malone,NBA,PF,205.7,117.5
Robert Parish,NBA,C,215.9,110.7
Kevin Garnett,NBA,PF,210.8,108.9
Nate Thurmond,NBA,C,210.8,102.1
Walt Bellamy,NBA,C,208.3,102.1
Wes Unseld,NBA,C,200.7,111.1
Hakeem Olajuwon,NBA,C,213.4,115.7
Dwight Howard,NBA,C,208.3,120.2
Shaquille O'Neal,NBA,C,215.9,147.4
John Stockton,NBA,PG,185.4,79.4
Jason Kidd,NBA,PG,193,95.3
Steve Nash,NBA,PG,190.5,80.7
Mark Jackson,NBA,PG,190.5,88.5
Magic Johnson,NBA,PG,205.7,99.8
Oscar Robertson,NBA,PG,195.6,93
Chris Paul,NBA,PG,185.4,79.4
LeBron James,NBA,SF,205.7,113.4
Isiah Thomas,NBA,PG,185.4,81.6
Gary Payton,NBA,PG,193,86.2
Andre Miller,NBA,PG,190.5,90.7
Rod Strickland,NBA,PG,190.5,83.9
Maurice Cheeks,NBA,PG,185.4,81.6
Russel Westbrook,NBA,PG,190.5,90.7
Rajon Rondo,NBA,PG,185.4,81.6
Ray Lewis,NFL,LB,185.4,108.9
London Fletcher,NFL,LB,177.8,109.8
Derrick Brooks,NFL,LB,182.9,106.6
Donnie Edwards,NFL,LB,188,100.7
Zack thomas,NFL,LB,180.3,103.4
Keith Brooking,NFL,LB,188,108.9
Karlos Dansby,NFL,LB,193,113.4
Junior Seau,NFL,LB,190.5,113.4
Brian Urlacher,NFL,LB,193,117
Ronde Barber,NFL,DB,177.8,83.5
Lawyer Milloy,NFL,DB,182.9,95.7
Takeo Spikes,NFL,LB,188,109.8
James Farrior,NFL,LB,188,110.2
Charles Woodson,NFL,DB,185.4,95.3
Antoine Bethea,NFL,DB,180.3,93.4
Derrick Johnson,NFL,LB,190.5,109.8
Lance Briggs,NFL,LB,185.4,110.7
Antoine Winfield,NFL,DB,175.3,81.6
Rodney Harrison,NFL,DB,185.4,99.8
Brian Dawkins,NFL,DB,182.9,95.3
※NBA選手はポジションがばらけるようAssistsとReboundsの歴代15位までを、
NFL選手はTacklesの歴代20位まで(ディフェンスの選手)をデータベース化しています。
縦軸を体重、横軸を身長としてプロットすると
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
df_athelete = pd.read_csv(f'./nba_nfl_1.csv') # データ読込
sns.scatterplot(x='height', y='weight', data=df_athelete, hue='league') # 説明変数と目的変数のデータ点の散布図をプロット
plt.xlabel('height [cm]') # X軸のラベル(身長)
plt.ylabel('weight [kg]') # Y軸のラベル(体重)
このデータをscikit-learnを使ってサポートベクターマシンで分類し、
mlxtend(参考)で決定境界を可視化します。
SVMを実行する前は、事前に説明変数を標準化する必要があることに注意してください
import numpy as np
from sklearn.svm import SVC
from mlxtend.plotting import plot_decision_regions
from sklearn.preprocessing import StandardScaler
def label_str_to_int(y): # 目的変数をstr型→int型に変換(plot_decision_regions用)
label_names = list(dict.fromkeys(y[:, 0]))
label_dict = dict(zip(label_names, range(len(label_names))))
y_int=np.vectorize(lambda x: label_dict[x])(y)
return y_int
def legend_int_to_str(ax, y): # 凡例をint型→str型に変更(plot_decision_regions用)
hans, labs = ax.get_legend_handles_labels()
ax.legend(handles=hans, labels=list(dict.fromkeys(y[:, 0])))
X = df_athelete[['height','weight']].values # 説明変数(身長、体重)
y = df_athelete[['league']].values # 目的変数(種目)
stdsc = StandardScaler() # 標準化用インスタンス
X = stdsc.fit_transform(X) # 説明変数を標準化
y_int = label_str_to_int(y) # 目的変数をint型に変換
model = SVC(kernel='linear', C=1000) # 線形SVMを定義(後述のソフトマージンの影響を減らすためCは大きく)
model.fit(X, y_int) # SVM学習を実行
ax = plot_decision_regions(X, y_int[:, 0], clf=model, zoom_factor=2) #決定境界を可視化
plt.xlabel('height [normalized]') # x軸のラベル
plt.ylabel('weight [normalized]') # y軸のラベル
legend_int_to_str(ax, y) # 凡例をint型→str型に変更
※なお、label_str_to_int()およびlegend_int_to_str()メソッドですが、mlxtendでの決定境界表示はクラスラベルをint型に変更しないとエラーが出る謎仕様 特殊な仕様となっているため、一度int型に変換してモデルを作成したのち、凡例のみstr型に表示を戻すための処理です。

直線で決定境界が引かれ、かつマージンが最大化されていることが分かります。
サポートベクターマシンの性能向上
こちらの記事で触れましたが、機械学習は推定性能を向上させるため、次のような機能に対応していることが一般的です。
A. 多次元説明変数:任意のn次元の説明変数に対応
B. 非線形:決定境界を直線(超平面)以外の柔軟な形状に変化させる
C. 汎化性能向上:学習データへの過剰適合を防ぎ、未知データに対する推定能力を向上させる
SVMにおいても、A~Cに対応するアルゴリズムが付加されているので、以下で詳説します。
A. 多次元説明変数
以下の式では、大文字はベクトルを表します(参考)
前述の2次元の例では直線で引いた決定境界ですが、3次元以上で一般化すると、超平面で境界を引くこととなります。
超平面の方程式は、
{W^T}X_i+w_0=0
で表されます。
この超平面と点Xiとの距離は、
d = \frac{|w_1x_1 + w_2x_2... + w_nx_n + w_0|}{\sqrt{w_1^2+w_2^2...+w_n^2}} = \frac{|W^TX_i + w_0|}{||W||}
となります。
この距離の最小値をマージンmとした上で、
y_i= \left\{
\begin{array}{ll}
1 & (X_iがクラス1のとき) \\
-1 & (X_iがクラス2のとき)
\end{array}
\right.
となるyiを定義すると、
マージンmは下式のように表わされます
\frac{y_i(W^TX_i + w_0)}{||W||} \geq m \quad (i = 1, 2, ...N)
両辺をmで割って変形すると
y_i\biggl(\biggl(\frac{W}{m||W||}\biggl)^TX_i + \frac{w_0}{m||W||}\biggl) - 1 \geq 0
ここで
新たなW = \frac{W}{m||W||}\\
新たなw_0 = \frac{w_0}{m||W||}
となるよう標準化すると、
(最初の式のように、Wは平面を張るベクトルの方向が同じであれば大きさは問わないので、計算しやすいよう$||W||=1/m$となるよう標準化)
y_i({W^T}X_i+w_0)-1 \geq 0
となります。
この条件下で、マージン
m=\frac{1}{||W||}
を最大化すれば良いのですが、
この後の計算をしやすくするため、
\frac{1}{2}{||W||}^2
を最小化する問題に置き換えます。
するとマージン最大化の条件式は、
g_i(W,w_0)=y_i({W^T}X_i+w_0)-1 \geq 0
(※等号が成り立つときが、決定境界に最も近い点=サポートベクター)
の制約条件下で、
f(W)=\frac{1}{2}{||W||}^2
を最小化する問題となります。
不等号条件化での最小化問題なので、ラグランジュの未定乗数法に基づき
L(W,w_0,\alpha)=f(W)-\sum_{i=1}^{n}\alpha_i g_i(W,w_0)\\
=\frac{1}{2}{||W||}^2-\sum_{i=1}^{n}\alpha_i(y_i({W^T}X_i+w_0)-1)
の極値を求めます。
極値を求めるためにW, w0で偏微分し、
\frac{\partial L}{\partial W}=0 \quad \Rightarrow \quad W=\sum_{i=1}^{n}\alpha_i y_i X_i\\
\frac{\partial L}{\partial w_0}=0 \quad \Rightarrow \quad \sum_{i=1}^{n}\alpha_i y_i=0
となるので、これらをLの式に代入し、KKT条件の式(αi≧0)も追加すると、
\sum_{i=1}^{n}\alpha_i y_i=0\\
\alpha_i \geq 0
の制約条件下で
L(\alpha)=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i \alpha_j y_i y_j X_i^T X_j - \sum_{i=1}^{n}\alpha_i
を最小化する問題となります。
以降はαに関する2次計画問題に帰結するので省略しますが、興味がある方は[こちらのサイトが分かりやすいです]
(https://satopirka.com/2018/12/theory-and-implementation-of-linear-support-vector-machine/)
上記手法により、多次元説明変数においてもマージンを最大化する超平面(の係数W)を求めることができます。
B. 非線形
先ほどのNBA選手とNFL選手の識別の例において、NFL選手のデータを、より体重の軽い傾向にあるオフェンス(ライン以外)の選手に置き換えます
name,league,position,height,weight
Wilt Chambelain,NBA,C,215.9,113.4
Bill Russel,NBA,C,208.3,97.5
Kareem Abdul-Jabbar,NBA,C,218.4,102.1
Elvin Hayes,NBA,PF,205.7,106.6
Moses Malone,NBA,C,208.3,97.5
Tim Duncan,NBA,PF,210.8,113.4
Karl Malone,NBA,PF,205.7,117.5
Robert Parish,NBA,C,215.9,110.7
Kevin Garnett,NBA,PF,210.8,108.9
Nate Thurmond,NBA,C,210.8,102.1
Walt Bellamy,NBA,C,208.3,102.1
Wes Unseld,NBA,C,200.7,111.1
Hakeem Olajuwon,NBA,C,213.4,115.7
Dwight Howard,NBA,C,208.3,120.2
Shaquille O'Neal,NBA,C,215.9,147.4
John Stockton,NBA,PG,185.4,79.4
Jason Kidd,NBA,PG,193,95.3
Steve Nash,NBA,PG,190.5,80.7
Mark Jackson,NBA,PG,190.5,88.5
Magic Johnson,NBA,PG,205.7,99.8
Oscar Robertson,NBA,PG,195.6,93
Chris Paul,NBA,PG,185.4,79.4
LeBron James,NBA,SF,205.7,113.4
Isiah Thomas,NBA,PG,185.4,81.6
Gary Payton,NBA,PG,193,86.2
Andre Miller,NBA,PG,190.5,90.7
Rod Strickland,NBA,PG,190.5,83.9
Maurice Cheeks,NBA,PG,185.4,81.6
Russel Westbrook,NBA,PG,190.5,90.7
Rajon Rondo,NBA,PG,185.4,81.6
Drew Brees,NFL,QB,182.9,94.8
Tom Brady,NFL,QB,193,102.1
Payton Manning,NFL,QB,195.6,104.3
Brett Favre,NFL,QB,188,100.7
Philip Rivers,NFL,QB,195.6,103.4
Dan Marino,NFL,QB,193,101.6
Ben Roethlisberger,NFL,QB,195.6,108.9
Eli Manning,NFL,QB,195.6,99.8
Matt Ryan,NFL,QB,193,98.4
John Elway,NFL,QB,190.5,97.5
Emmitt Smith,NFL,RB,175.3,100.2
Walter Payton,NFL,RB,177.8,90.7
Frank Gore,NFL,RB,175.3,96.2
Barry Sanders,NFL,RB,172.7,92.1
Adrian Peterson,NFL,RB,185.4,99.8
Curtis Martin,NFL,RB,180.3,95.3
LaDainian Tomlinson,NFL,RB,177.8,97.5
Jerome Bettis,NFL,RB,180.3,114.3
Eric Dickerson,NFL,RB,190.5,99.8
Tony Dorsett,NFL,RB,180.3,87.1
Jerry Rice,NFL,WR,188,90.7
Larry Fitzgerald,NFL,WR,190.5,98.9
Terrell Owens,NFL,WR,190.5,101.6
Randy Moss,NFL,WR,193,95.3
Isaac Bruce,NFL,WR,182.9,85.3
Tony Gonzalez,NFL,TE,195.6,112
Tim Brown,NFL,WR,182.9,88.5
Steve Smith,NFL,WR,175.3,88.5
Marvin Harrison,NFL,WR,182.9,83.9
Reggie Wayne,NFL,WR,182.9,92.1
※NFL選手は、Passing(主にQB), Rushing(主にRB), Receiving(主にWR)の各ヤード数歴代10位までをデータベース化しています
df_athelete = pd.read_csv(f'./nba_nfl_2.csv')
sns.scatterplot(x='height', y='weight', data=df_athelete, hue='league') # 説明変数と目的変数のデータ点の散布図をプロット
plt.xlabel('height [cm]') # x軸のラベル
plt.ylabel('weight [kg]') # y軸のラベル
残念ながら直線(線形)の決定境界では分けられないようです。
前述のSVMは線形分離可能な場合のみを想定したアルゴリズムのため、線形分離不可のときは、
① カーネルトリックによる非線形決定境界 → 「B.非線形」に対応する工夫
② ソフトマージン → 「C.汎化性能」に対応する工夫
という2種類の対処法いずれか(あるいは両方)を実施する必要があります。
本節では①に関して解説します。
カーネルトリックとは?
例えば、下図の青い点と赤い点とを分類したい場合を考えます。

見ての通り、xy座標系では線形(直線)での分離は困難です。
では
z=x^2+y^2
として、z軸を追加した座標系でプロットしてみるとどうなるでしょう?

上図のように、z軸を追加することで線形分離可能となり、
この分離面を元のxy座標系に逆変換すると、円形(=非線形)の決定境界を引くことに相当します。
このように、元の座標軸(特徴量)を組み合わせた高次元の座標系への変換Φを行うことで、
線形分離不可能な場合でも、非線形な決定境界による分類を実現できます。
このとき、xを射影して$\Phi(x)$に変換するため、前述のラグランジュの未定乗数法で最小化する関数
L(\alpha)=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i \alpha_j y_i y_j X_i^T X_j - \sum_{i=1}^{n}\alpha_i
は、
L(\alpha)=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i \alpha_j y_i y_j \phi(X_i)^T \phi(X_j) - \sum_{i=1}^{n}\alpha_i
へと置き換えられます。
ただし、
\phi(X_i)^T \phi(X_j)
の部分が計算コストが大きいため、
一般的には写像Φは直接定義せず、
カーネル関数
K(X_i,X_j)=\phi(X_i)^T \phi(X_j)
を定義して計算することが多いです。このカーネル関数による変換法をカーネルトリックと呼びます。
カーネル関数の中でも特によく使われるのが
K(X_i,X_j)=exp\biggl(-\frac{||X_i-X_j||^2}{2\sigma^2}\biggl)\\
=exp \Bigl(-\gamma||X_i-X_j||^2 \Bigl)
で定義されるRBFカーネル(Radial Basis Function kernel)です。
この式中に含まれる$\gamma$が、ハイパーパラメータの1つとなります
scikit-learn公式の説明を見ると、$\gamma$は「1点の学習データが、識別面に影響を与える距離」を表すパラメータと記載されており、数式で分散σ2の逆数となっていることからも、何となくイメージが付くかと思います。
γが大きくなるほど、1点の影響範囲が小さい = 曲率が大きな識別面となる
というようなイメージです。
先ほどのNBA選手とNFL選手での分類を、$\gamma$(scikit-learnでは"gamma")を変えてRBFカーネルで学習してみます。
X = df_athelete[['height','weight']].values # 説明変数(身長、体重)
y = df_athelete[['league']].values # 目的変数(種目)
stdsc = StandardScaler() # 標準化用インスタンス
X = stdsc.fit_transform(X) # 説明変数を標準化
y_int = label_str_to_int(y)
for gamma in [10, 1, 0.1, 0.01]: # gammaを変えてループ
model = SVC(kernel='rbf', gamma=gamma) # RBFカーネルのSVMをgammaを変えて定義
model.fit(X, y_int) # SVM学習を実行
ax = plot_decision_regions(X, y_int[:, 0], clf=model, zoom_factor=2)
plt.xlabel('height [normalized]')
plt.ylabel('weight [normalized]')
legend_int_to_str(ax, y)
plt.text(np.amax(X[:, 0]), np.amin(X[:, 1]), f'gamma={model.gamma}, C={model.C}', verticalalignment='bottom', horizontalalignment='right') # gammaとCを表示
plt.show()
※scikit-learnのSVMはソフトマージンのため、後述のCも含まれていることにご注意ください
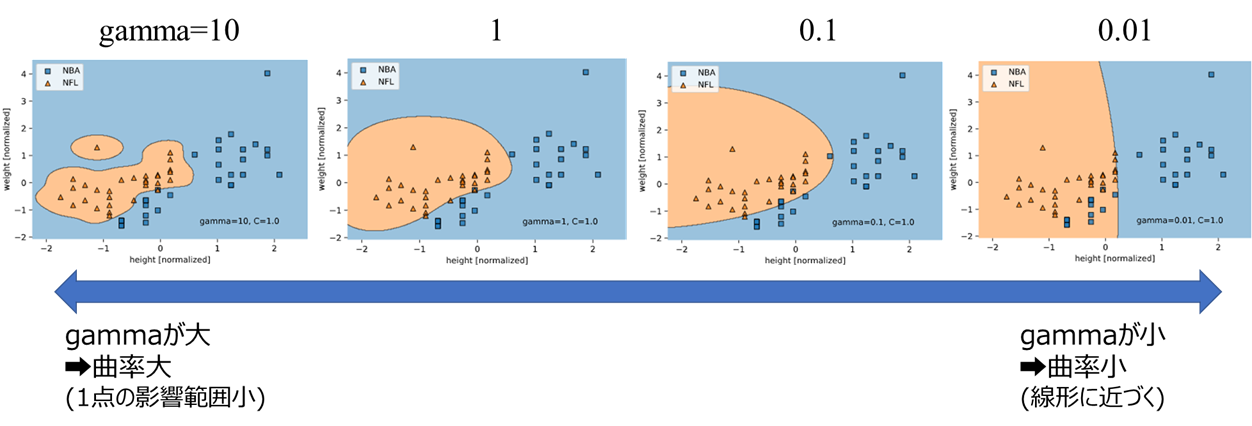
gamma $(\gamma)$が小さくなるほど曲率が小さくなって線形に近づき、gammaが大きくなるほど曲率が大きくなることが分かります。
ここからも、gammaが「どれくらい非線形か」を調整するパラメータであることが分かるでしょう
C. 汎化性能
前述のように、SVMには線形分離不可能な場合に対応するために「ソフトマージン」という手法が適用できます(詳細はこちらが詳しいです)
Aで登場したマージン最大化の制約条件
y_i({W^T}X_i+w_0)-1 \geq 0
ですが、これは「誤分類は1個も許さない」(ハードマージン)という意味合いの式となっています。
これでは線形分離不可能な場合、この制約条件を満たせず学習ができなくなってしまうため、
下式で表すスラック変数$\xi_i$を導入し、
\xi_i = max\bigl\{0, 1 - y_i(W^TX_i + w_0)\bigr\}
制約条件を下式のように書き換え、ある程度の誤分類を許容するようにします(ソフトマージン)
y_i({W^T}X_i+w_0)-1+\xi_i \geq 0
上式から読みとれるスラック変数$\xi_i$の性質として
・ξi = 0のとき、本来の定義でのマージン範囲内(線形分離可)
・0 < ξi < 1のとき、本来の定義でのマージンを超えて決定境界に近づく(誤分類ではない)
・ξi > 1のとき、決定境界を飛び越えて誤分類が発生する
・ξiが大きくなるほど、誤分類の度合いが大きくなる
があり、誤分類を防ぐ観点では、スラック変数は小さくしたい変数であることがわかります。
そこで、マージン最大化の式において最小化すべき関数
f(W)=\frac{1}{2}{||W||}^2
に、スラック変数の総和に係数Cを掛けて足し合わせた
f(W)=\frac{1}{2}{||W||}^2+C\sum_{i=1}^{n}\xi_i
を新たに最小化すべき関数として定義することで、
「マージン最大化」と「誤分類許容」のバランスを取って学習することができます。
この誤分類許容のバランスを決める係数Cが、ハイパーパラメータの1つとなります
基本的にはCが大きいほど誤分類の最小化関数に対する影響が大きくなるため、
Cが大:誤分類を許容しない傾向(過学習寄り)
Cが小:誤分類を許容する傾向(未学習=汎化寄り)
となります
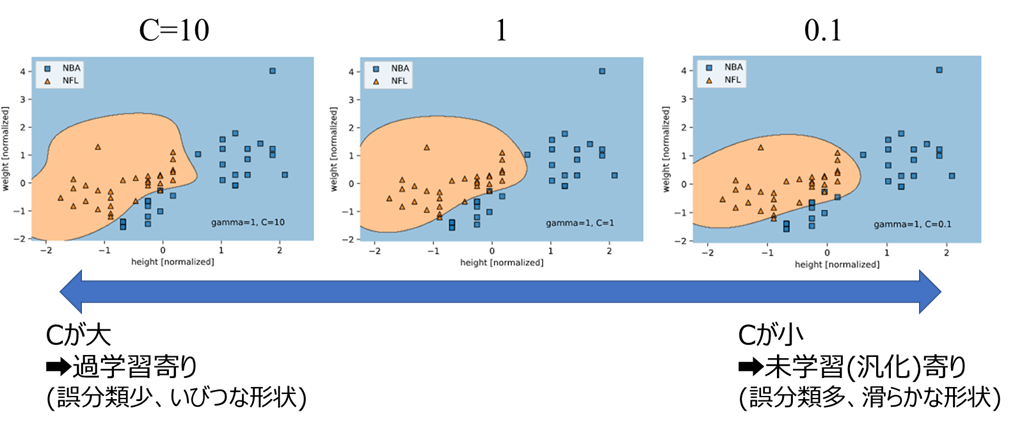
先ほどのNBA選手とNFL選手の分類を、Cを変えてRBFカーネルで学習してみます。
(gammaは0.01で固定)
for C in [10, 1, 0.1]: # Cを変えてループ
model = SVC(kernel='rbf', gamma=0.01, C=C) # RBFカーネルのSVMをCを変えて定義
model.fit(X, y_int) # SVM学習を実行
ax = plot_decision_regions(X, y_int[:, 0], clf=model, zoom_factor=2)
plt.xlabel('height [normalized]')
plt.ylabel('weight [normalized]')
legend_int_to_str(ax, y)
plt.text(np.amax(X[:, 0]), np.amin(X[:, 1]), f'gamma={model.gamma}, C={model.C}', verticalalignment='bottom', horizontalalignment='right') # gammaとCを表示
plt.show()
Cが大きいほど、誤分類は少ないがいびつな決定境界(過学習寄り)
Cが小さいほど、誤分類は多いが滑らかな決定境界(未学習=汎化寄り)
となっていることが分かります。
まとめ
・サポートベクターマシンは、決定境界から最近点までの距離(マージン)を最大化するアルゴリズム
・カーネルトリックで、非線形の決定境界に対応
・カーネルトリックでは、RBFカーネルがよく使われる
・RBFカーネルに対応するハイパーパラメータは"gamma"、小さいほど線形に近づく
・ソフトマージンで、一定の誤分類を許容して汎化性を向上
・ソフトマージンに対応するハイパーパラメータは"C"、小さいほど汎化(未学習)寄りとなる
おわりに
コードおよび使用データはこちらにアップロードしております
(VSCodeでの動作推奨。101行目以降が本記事のコードに該当しますが、1行目から順番に実行してください)
パラメータCとgammaをどの値に設定すれば良いのか?が気になる方も多いと思いますが、具体的な方法は以下の記事にまとめました。こちらもぜひご覧ください
2021/2/9修正:標準化について
SVMは前処理として標準化が必要です。記載が漏れており申し訳ないです
標準化とは平均が0、標準偏差が±1となるよう説明変数をスケール変換することです。
あるデータxの平均をμ、標準偏差をσとすると、xを標準化したx'は
x'=\frac{x-\mu}{\sigma}
で表されます
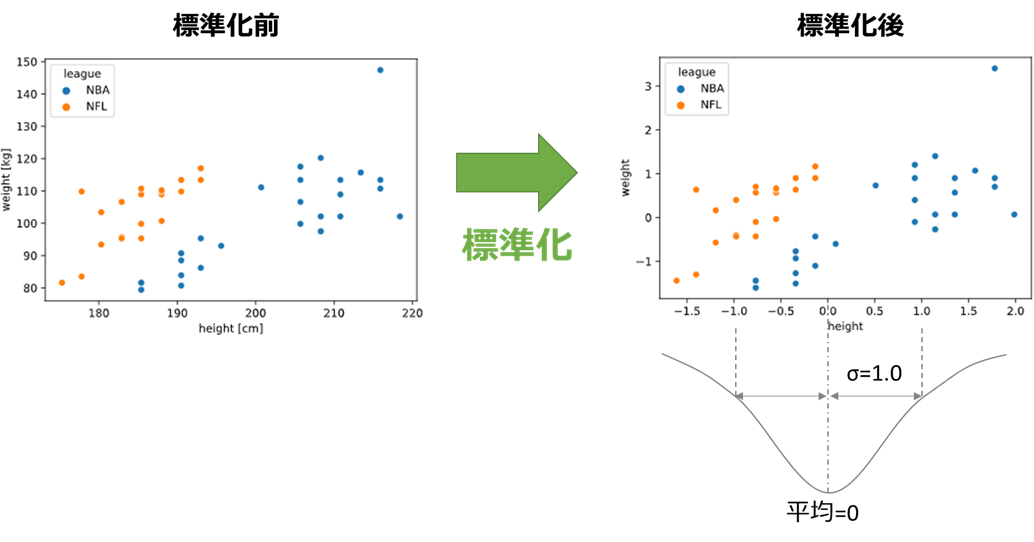
SVMのように特徴量空間での距離に基づいたアルゴリズムでは、標準化により説明変数間のスケールを揃えないと、変数間の評価に偏りが生じてしまい、うまく精度が出ません。
本文中のコードにも、標準化処理を追記しました