はじめに
今回は機械学習のアルゴリズムの一つであるサポートベクトルマシンについての理論をまとめていきます。
お付き合い頂ければ幸いです。
サポートベクトルマシンとは
サポートベクトルマシン(svm)は汎化性能や応用分野の広さから、データ分析の現場でよく用いられる機械学習のアルゴリズムの一つです。
マージン最大化と呼ばれる考えに基づき、主に2値分類問題に用いられます。多クラス分類や回帰問題への応用も可能です。
計算コストが他の機械学習のアルゴリズムと比較して大きいため、大規模なデータセットには向かないという弱点があります。
線形分離可能(一つの直線で二つに分けられる)なデータを前提としたマージンをハードマージン、線形分離不可能なデータを前提として、誤判別を許容するマージンをソフトマージンと呼びます。
線形分離可能を一つの直線で二つに分けられると書きましたが、これは2次元のデータにおいてのみであるので、線形分離可能の概念を一般化してn次元空間上の集合をn-1次元の超平面で分離できることを線形分離可能と定義します。
二次元の平面上のデータを一次元の線で分類できるとき、それは線形分離可能であるといえます。また、三次元の空間上のデータを二次元の平面で分類できるときも、線形分離可能であるといえます。
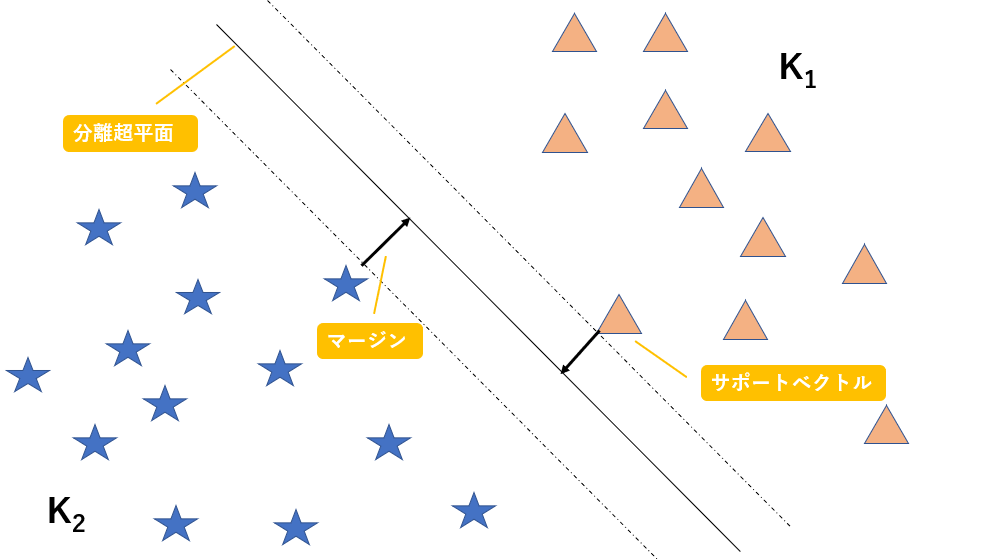
このように、n次元のデータを分類するn-1次元の平面(厳密には平面ではない)を分離超平面と呼び、また分離超平面とその分離超平面に最も近いデータとの距離をマージンと呼び、このマージンを最大化することがこのアルゴリズムの目標になります。
また、分離超平面に最も近いでデータのことをサポートベクトルと呼びます。以下に図解します。
図に示すマージンを最大化するような超平面を作成することで精度を上昇させることができるのは、直感的に明らかですよね。
図示するために今回は二次元でデータを表現しましたが、n次元空間上のデータをn-1次元の超平面で分割していると考えてください。
二次元の数ベクトル空間上においては、上の図のように二つのデータを分割する直線を$ax + by + c = 0$と表すことができ、パラメータ$a, b, c$を調整することで全ての直線を表すことができます。
今回はn次元数ベクトル空間上の超平面を想定しているので、その超平面の式を以下数式で与えられます。今、全部でN個のデータが存在する場合を考えます。
$$W^TX_i + b = 0 \quad (i = 1, 2, 3, ...N)$$
$W^TX_i+b=0$の部分を計算すると、$w_1x_1 + w_2x_2 + ...w_nx_n+b=0$となり、これは二次元における直線の式である$ax + by + c = 0$をn次元に拡張した超平面の式であることが感覚的に理解できると思います。
図の三角のデータは$K_1$の集合に属していて、図の星のデータは$K_2$の集合に属していると考えると、以下の式を満たすことが分かります。
W^TX_i + b > 0 \quad (X_i \in K_1)\\
W^TX_i + b < 0 \quad (X_i \in K_2)
この式をまとめて表すためにラベル変数tを導入します。
i番目のデータ$x_i$がクラス1に属するときに$t_i=1$、クラス2に属するときに$t_i=-1$とします。
t_i = \left\{
\begin{array}{ll}
1 & (X_i \in K_1) \\
-1 & (X_i \in K_2)
\end{array}
\right.
このように定義した$t_i$を用いると、条件式を以下のように表すことができます。
$$t_i(W^TX_i + b) > 0 \quad (i = 1, 2, 3, ...N)$$
このように、条件式を一行で表すことができました。
マージンはn次元空間上の点と超平面との距離になるので、点と直線の距離について復習しましょう。二次元の点と直線の距離は、点を$A(x0,y0)$ 、直線を$l:ax+by+c=0$とすると以下の式で表されましたね。
d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2+b^2}}
n次元空間上の1点と超平面との距離は以下の式で表されます。
d = \frac{|w_1x_1 + w_2x_2... + w_nx_n + b|}{\sqrt{w_1^2+w_2^2...+w_n^2}} = \frac{|W^TX_i + b|}{||w||}
よって、ここまでの式からマージンMを最大化するという条件は以下の式で表されます。
max_{w, b}M, \quad \frac{t_i(W^TX_i + b)}{||W||} \geq M \quad (i = 1, 2, 3, ...N)
ちょっとよく分からないと思うので、解説します。
あるデータ$X_a$を選んだときの、$X_a$と超平面$W^TX + b=0$との距離は、$ \frac{t_i(W^TX_a + b)}{||W||}$と表されますね。
$|W^TX_a + b|$をラベル変数tを用いて$t_i(W^TX_a + b)$と表しています。
また、$max_{w, b}M$は変数$w, b$のもとでMを最大化するという意味であり、$\frac{t_i(W^TX_i + b)}{||W||} \geq M $という条件は、超平面と全てのデータとの距離をマージンMよりも大きくするということを表しています。
よって、この数式を満たすMを求めるということが、サポートベクトルマシンを最適化するということになります。
ここで、$\frac{t_i(W^TX_i + b)}{||W||} \geq M $の両辺をMで割り、以下の条件を導入します。
\frac{W}{M||W||} = \tilde{W}\\
\frac{b}{M||W||} = \tilde{b}
すると、最適化問題の条件式は以下のように表されます。
t_i(\tilde{W^T}X_i + \tilde{b}) \geq 1
全てのデータに対して上の式は成り立ちますが、等号が成り立つときの$X_i$が最も近いデータの$X_i$になります。
つまり、マージンMを簡略化した $\tilde{M}$は以下の式で表されます。
\tilde{M} = \frac{t_i(\tilde{W^T}X_i + \tilde{b})}{||\tilde{W}||} = \frac{1}{||\tilde{W}||}
この式変形により、最適化問題は以下のようになります。
max_{\tilde{W}, \tilde{b}}\frac{1}{||\tilde{W}||}, \quad t_i(\tilde{W^T}X_i + \tilde{b}) \geq 1 \quad (i = 1, 2, 3, ...N)
結構難しくなってきましたね。頑張っていきましょう。
途中の式変形でチルダがついてしまいましたが、簡単のために取っ払いましょう。そして、$\frac{1}{||\tilde{W}||}$の部分については、ノルムの逆数を最大化するという意味ですので、簡単のためにノルムを二乗を最小化する問題に変換しましょう。ここの部分の式変形は少しごり押しです。後の計算を簡単にするために$\frac{1}{2}$をつけます。
min_{W, b}\frac{1}{2}||W||^2, \quad t_i(W^TX_i + b)\geq 1 \quad (i = 1, 2, 3, ...N)
上記の式を解くこと、つまり$t_i(W^TX_i + b)\geq 1$という条件の下で$\frac{1}{2}||W||^2$を最小化することによりマージンを最大化することができます。これが線形分離可能な場合の最適化問題の式になります。
しかし、この条件では線形分離可能な問題しか解くことができません。つまり、ハードマージンにしか適用できません。
上記の式の制約条件$t_i(W^TX_i + b)\geq 1$を緩めることで、線形分離不可能な問題(ソフトマージン)にも対応できるようにしましょう。
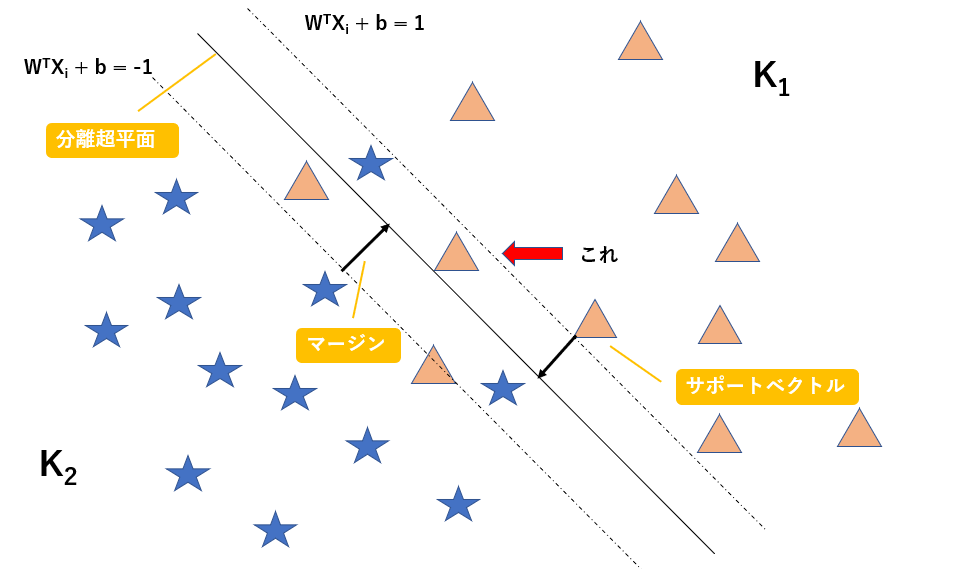
以下に図解します。
この図のように線形分離不可能な問題を考えます。図の赤矢印で示すように、マージンの内側にデータが入り込んでしまっています。
$W^TX_i + b = 1$を満たす超平面上にサポートベクトル(超平面に最も近いデータ)が存在するのはここまでの話から考えると当然ですね。
図の赤矢印で示すデータは$ t_i(W^TX_i + b)\geq 1$を満たしていませんが、$ t_i(W^TX_i + b)\geq 0.5$という条件なら満たすかもしれません。
よって、スラッグ変数$\xi$を導入することで制約条件を緩めることにしましょう。以下のように定義します。
t_i(W^TX_i + b)\geq 1 - \xi_i \\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}
以上の式より、データがマージンの内側にある場合にのみ、制約を緩めることにします。
よって、このスラッグ変数を導入することにより、マージン最適化問題は以下のようになります。
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\} \quad 制約条件\quad
t_i(W^TX_i + b)\geq 1 - \xi_i\\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}\\
i = 1, 2, 3, ... N
マージンを最大化しようとする、つまり$\frac{1}{2}||W||^2$を最小化すると当然マージンの中に入ってくるデータが増えるため、$C\sum_{i=1}^{N} \xi_i$が増加します。よって、この最適化問題は相反する二つの項のバランスを取りながら最小化をはかることになります。
Cハイパーパラメーターであり、私たちが調節しながらモデルを構築することになります。
終わりに
かなり長くなってきたので、今回はここまでになります。
次回の記事ではこの最適化問題の式の解き方やカーネル法についてまとめていきたいと思います。
お付き合いいただきありがとうございました。
よろしければ次回の記事もご覧ください。
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく②~ラグランジュの未定乗数法~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく②~ラグランジュの未定乗数法~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく③~カーネル法について~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく④~ソフトマージンとハードマージンの実装~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく⑤~カーネル法を用いた分類の実装~
Shopify アプリのご紹介
Shopify アプリである、「商品ページ発売予告アプリ | リテリア Coming Soon」は、商品ページを買えない状態のまま、発売日時の予告をすることができるアプリです。Shopify で Coming Soon 機能を実現することができます。