はじめに
今回は前回の記事の続きなります。
よろしければ以下の記事もご覧ください。
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく①~理論と数式編~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく②~ラグランジュの未定乗数法~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく③~カーネル法について~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく④~ソフトマージンとハードマージンの実装~
カーネル法を用いずに実装
今回は線形分離不可能な問題をカーネル法を用いずに分類していきます。
ここでは、カーネル関数を使わない方法を、カーネル法を使わないと定義しています。
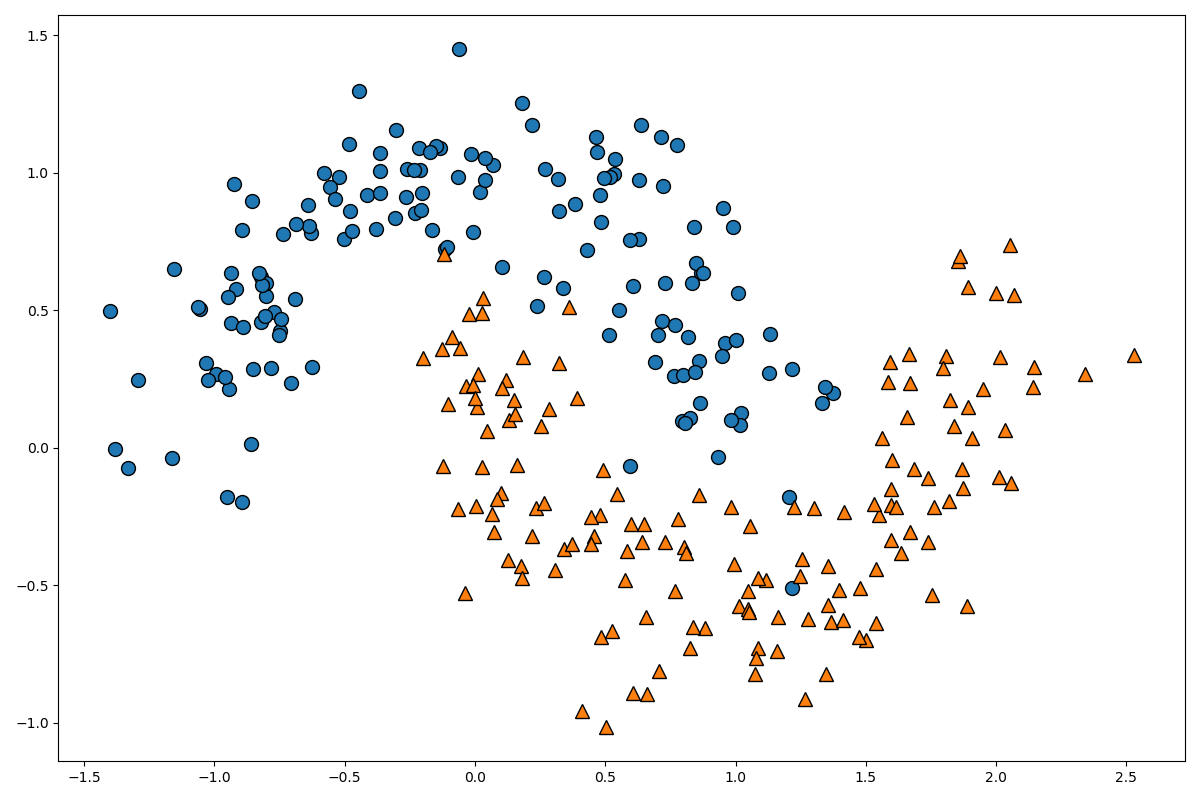
以下のコードでデータを準備して、図示しましょう。
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
moons = make_moons(n_samples=300, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
plt.figure(figsize=(12, 8))
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.plot()
plt.show()
make_moonsは、二次元の月のような形をしたデータを作成する関数です。
サンプル数とノイズを設定することができます。
図を見て頂ければ分かりますが、明らかに線形分離不可能ですよね。
この線形分離不可能なデータを線形分離可能なデータに変形するために、この入力空間のデータを高次元特徴空間のデータに写像しましょう。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)
これで、入力空間のデータを高次元特徴空間に写像することができました。
どのようなデータに写像されたか確認しましょう。
print(poly.get_feature_names())
print(X_train_poly.shape)
['1', 'x0', 'x1', 'x0^2', 'x0 x1', 'x1^2']
(225, 6)
このような形で、二次元入力空間が六次元特徴空間に拡張されています。
次のコードでデータを標準化します。
scaler = StandardScaler()
X_train_poly_scaled = scaler.fit_transform(X_train_poly)
X_test_poly_scaled = scaler.fit_transform(X_test_poly)
データの標準化とは、全てのデータに対して平均を引いた後に標準偏差で割ることで、データの平均を0、分散を1にすることです。
こちらの記事に分かりやすく書いていたので、参考にしてください。
それでは、次のコードでモデルを実装して評価します。
lin_svm = LinearSVC()
lin_svm.fit(X_train_poly_scaled, Y_train)
print(lin_svm.score(X_test_poly_scaled, Y_test))
0.84
ちょっと低いですね。もう少し高次元に写像しましょう。
しかし、高次元に写像して標準化するという処理が面倒くさいので、Pipelineというものを使用しましょう。
poly_scaler_svm = Pipeline([
('poly', PolynomialFeatures(degree=3)),
('scaler', StandardScaler()),
('svm', LinearSVC())
])
poly_scaler_svm.fit(X_train, Y_train)
print(poly_scaler_svm.score(X_test, Y_test))
0.9733333333333334
このように、Pipelineを用いると、データを高次元に写像して、標準化して、svmモデルに入れるという作業を簡略化して書くことができます。degree=3にすることで、より高次元の特徴空間に写像しています。
精度はかなり良いですね。高次元に写像するとかなり効果的です。
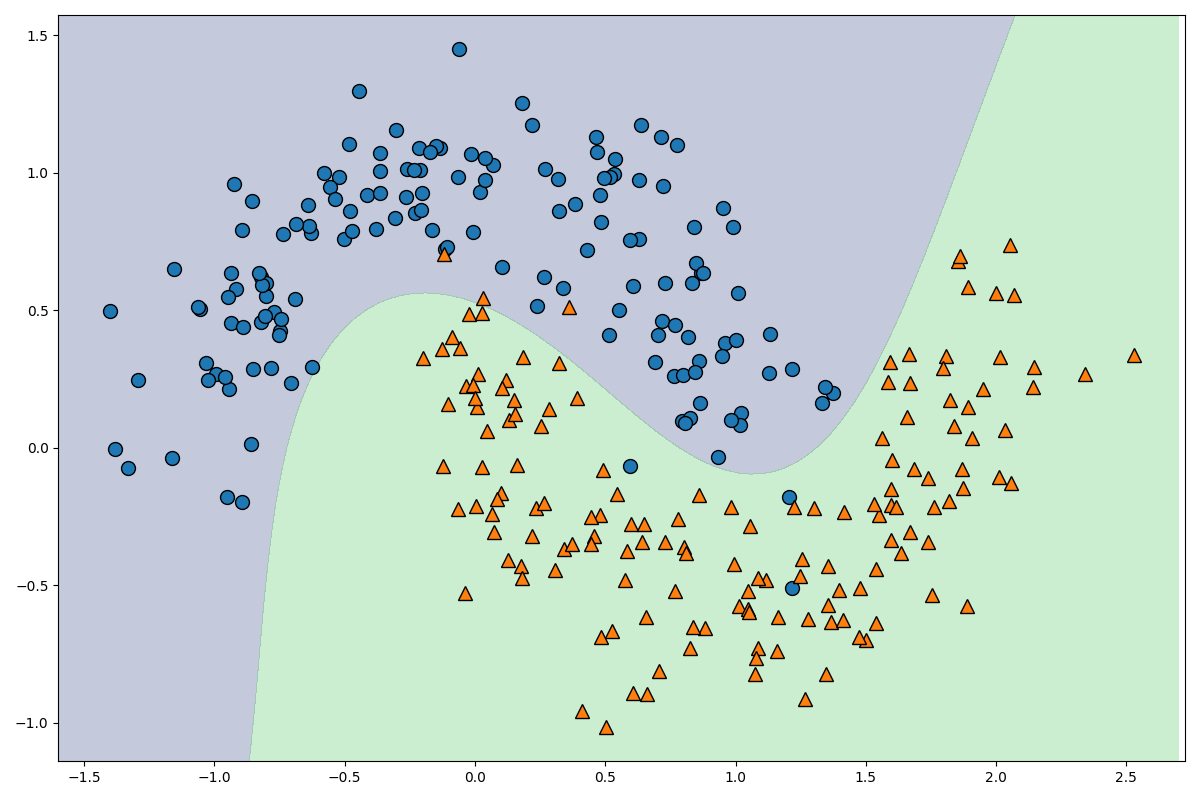
次は、この図を描画してみましょう。以下のコードです。
_x0 = np.linspace(-1.5, 2.7, 100)
_x1 = np.linspace(-1.5, 1.5, 100)
x0, x1 = np.meshgrid(_x0, _x1)
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
plt.figure(figsize=(12, 8))
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.show()
なかなかきれいな線が引けていることが確認できましたね。それではコードを解説します。
_x0 = np.linspace(-1.5, 2.7, 100)
_x1 = np.linspace(-1.5, 1.5, 100)
x0, x1 = np.meshgrid(_x0, _x1)
ここの部分のコードで格子点を作成しています。こちらの記事に分かりやすく書いてあるので、参考にしてください。
np.linspaceは第一引数に始点、第二引数に終点、第三引数に点の数を指定して、numpyのarrayを作成します。それをnp.meshgridに渡すことで、100×100の格子点を作成しています。
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
(x0.ravel()により、100×100のarrayを一次元配列に変換した後、reshape(-1, 1)により二次元の10000×1の行列に変換し、np.hstackによりaxis=1の水平方向に対して結合しています。つまり、Xは10000×2の行列になっています。
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
model.decision_function(X)により10000個の格子点と分離超平面との距離を求めて、それを100×100のデータに変換しています。
plt.contourfは等高線を図示する関数で、levelsにどの部分で色を変化させるかを指定できます。
以上でカーネル法を使わない実装は終了です。
カーネル法を用いた実装
それではカーネル法を用いて実装を行っていきます。
データを準備しましょう。ここまでは同じです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
moons = make_moons(n_samples=300, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
次のコードでモデルを実装しましょう。
karnel_svm = Pipeline([
('scaler', StandardScaler()),
('svm', SVC(kernel='poly', degree=3, coef0=1))
])
karnel_svm.fitX_train, Y_train()
SVCのkarnel引数にpolyを指定することで、多項式カーネルを指定し、degree=3を指定することで三次元までの写像を考えることができます。
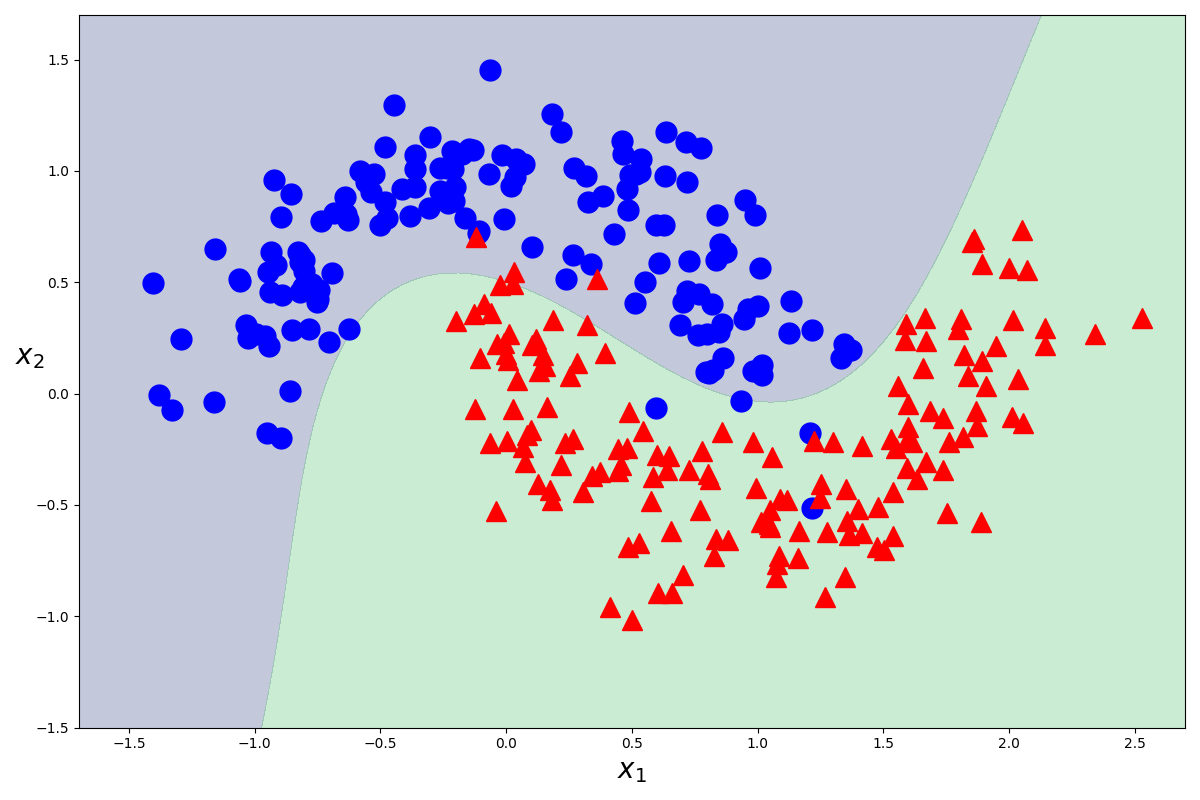
これでモデルの作成ができました。次は、このモデルを図示してみましょう。また同じことをするんですが、面倒くさいので関数にします。
def plot_decision_function(model):
_x0 = np.linspace(-1.7, 2.7, 100)
_x1 = np.linspace(-1.5, 1.7, 100)
x0, x1 = np.meshgrid(_x0, _x1)
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
def plot_dataset(x, y):
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'bo', ms=15)
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'r^', ms=15)
plt.xlabel('$x_1$', fontsize=20)
plt.ylabel('$x_2$', fontsize=20, rotation=0)
plt.figure(figsize=(12, 8))
plot_decision_function(karnel_svm)
plot_dataset(X, Y)
plt.show()
mglearnでプロットしても良かったのですが、今回はplt.plotでプロットしました。Y=0となるものを青色の丸で、Y=1となるものを赤色の三角で描画しています。
図から分かるように、カーネル法を使っても使わなくても同じ結果が返ってきます。しかし、カーネル法を用いた方が内部的に計算がかなり簡単になっているので、できるだけカーネル法を使った方が良い気がします。
どのように簡単になるのかはこちらの記事を参考にしてください。
終わりに
ここまでお付き合い頂きありがとうございました。
お疲れさまでした。