はじめに
今回の記事は前回の記事の続きになっています。
よろしければ以下の記事もご覧ください。
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく①~理論と数式編~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく②~ラグランジュの未定乗数法~
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく③~カーネル法について~
分類問題:ハードマージン
線形分離可能なデータを分離するsvmを実装していきます。
用いるデータはiris(アヤメ)データセットです。
iris(アヤメ)データセットについて
irisデータは、アヤメという花の品種のデータです。
アヤメの品種であるSetosa、Virginica、Virginicaの3品種に関するデータが50個ずつ、全部で150個のデータです。
実際に中身を見ていきましょう。
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
print(iris_df.head())
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
iris.feature_namesに各々のカラム名が格納されているので、それをpandasのDataframeの引数に渡すことで上のようなデータを出力できます。
Sepal Lengthはがく弁の長さが、Sepal Widthにはがく弁の幅が、Petal lengthには花びらの長さが、Petal Widthには花びらの幅のデータが格納されています。
以下のようにすれ正解ラベルを表示できます。
print(iris.target)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
このように、アヤメの品種であるsetosa、versicolor、virginicaをそれぞれ0, 1, 2としています。
アヤメのデータについての説明はここまでです。
実装
以下のコードでデータセットを作成しましょう。
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
import mglearn
iris = load_iris()
X = iris.data[:100, 2:]
Y = iris.target[:100]
print(X.shape)
print(Y.shape)
(100, 2)
(100,)
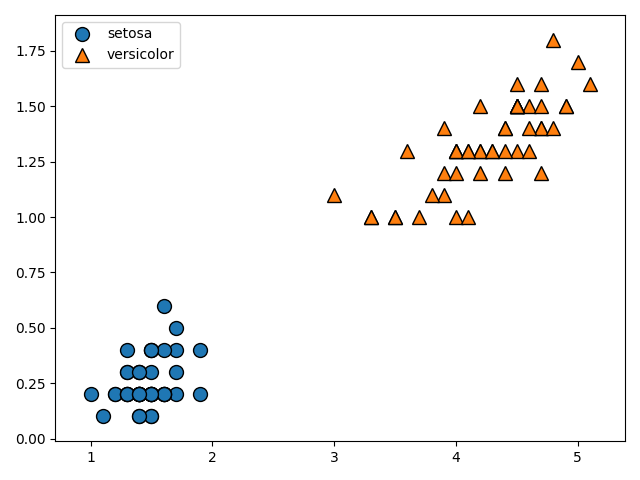
今回はsetosa、versicolorのpetal lengthとpetal widthのデータを用いて分類を行います。
以下のコードでデータの描画を行います。
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)のコードは第一引数をX軸、第二引数にY軸、第三引数に正解ラベルをとって、scatterプロットを行います。
loc='best'により、凡例がグラフの邪魔にならない位置にくるように調整しています。
上のデータから、明らかに直線で分離できることが分かりますね。むしろ簡単すぎるくらいです。
次のコードでモデルを作成しましょう。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
svm = LinearSVC()
svm.fit(X_train, Y_train)
モデルの作成自体はこのコードで終わりです。簡単ですね。
以下のコードでモデルがどのような形になったのかを図示しましょう。
plt.figure(figsize=(10, 6))
mglearn.plots.plot_2d_separator(svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
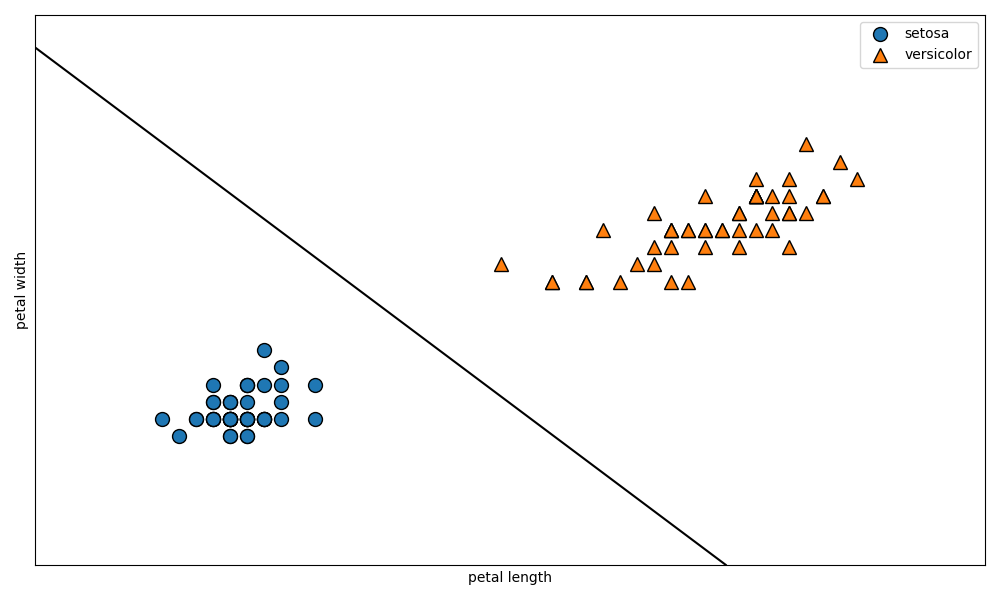
しっかりとデータを分ける境界線が作成されていることが確認できますね。
mglearn.plots.plot_2d_separator(svm, X)の部分は少し分かりにくいと思うので解説します。定義となるコードを確認しましょう。
plot_2d_separator(classifier, X, fill=False, ax=None, eps=None, alpha=1,cm=cm2, linewidth=None, threshold=None,linestyle="solid"):
第一引数に分類モデルを渡して、第二引数に元のデータを渡すと境界線を引いてくれる関数ですね。
ここまでで、線形分離可能な問題におけるsvmのモデルの実装は終了です。
分類問題: ソフトマージン
今回はソフトマージンの問題について取り扱います。
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
import mglearn
iris = load_iris()
X = iris.data[50:, 2:]
Y = iris.target[50:] - 1
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.legend(['versicolor', 'virginica'], loc='best')
plt.show()
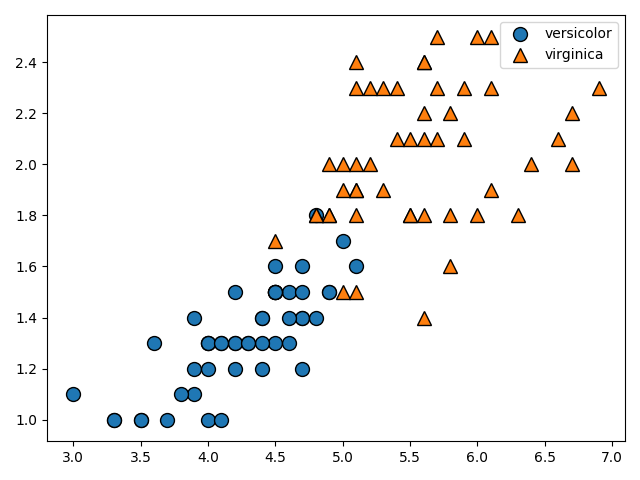
今度はversicolorとverginicaのpetal lengthとpetal widthについてのデータをプロットしています。
完全に線形分離することは不可能な問題ですね。
ここでソフトマージンの式を復習です。導出はこちらの記事を参考にしてください。
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\} \quad \quad
t_i(W^TX_i + b)\geq 1 - \xi_i\\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}\\
i = 1, 2, 3, ... N
データがマージンの内側に入り込んでしまうので、$ C\sum_{i=1}^{N} \xi_i$の項により制限を緩めているのでしたね。
このCの値はskleaarnにおいて、デフォルトで1.0になっています。この数値を変化させて、図がどう変わるのか確認してみましょう。以下のコードで、引数に与えたモデルの境界線をプロットする関数を定義します。
def make_separate(model):
mglearn.plots.plot_2d_separator(svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
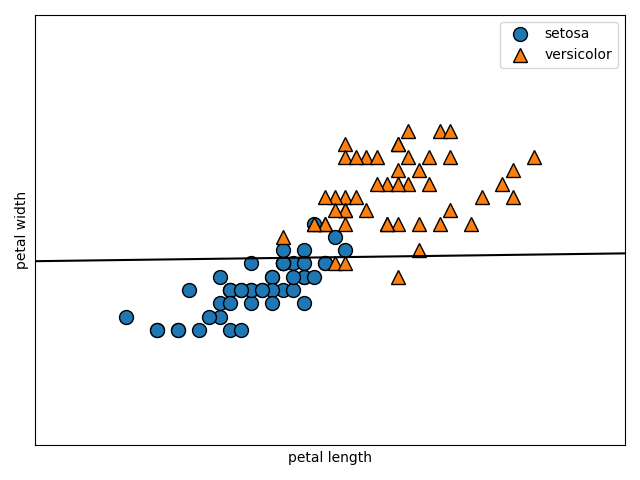
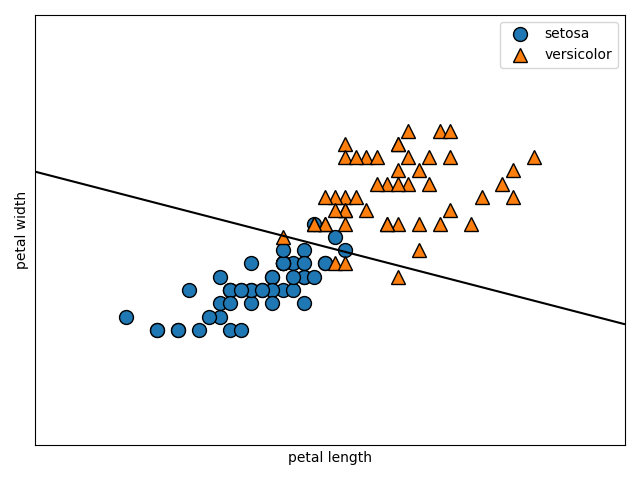
以下のコードで図を描画しましょう。C=0.1とします。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
svm = LinearSVC(C=0.1)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
0.96
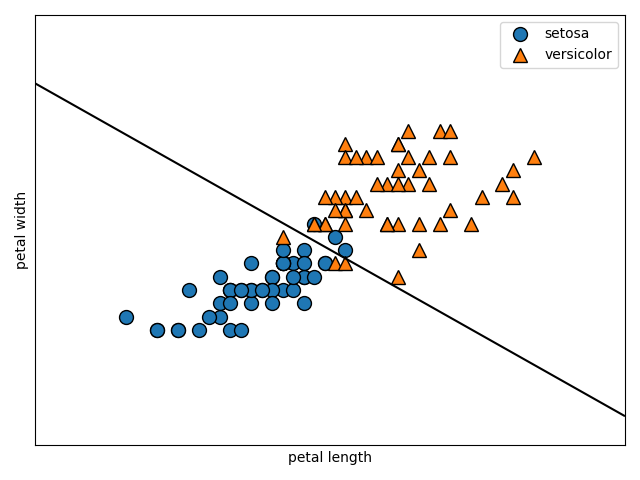
次はC=1.0です。
svm = LinearSVC(C=1.0)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
1.0
次はC=100です。
svm = LinearSVC(C=100)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
1.0
適切なCを設定するのが大切ですね。色々変えながら様子を見ていくのがよさそうです。
ここまででソフトマージンの実装は終了です。
終わりに
ここまでで今回の記事は終了です。
お疲れさまでした。
よろしければ次回の記事もご覧ください。
[機械学習]サポートベクトルマシン(SVM)について、できるだけ分かりやすくまとめていく⑤~カーネル法を用いた分類の実装~