Pythonで非線形関数モデリング

やること

Pythonで観測値（x,yのセット）を指定した関数で近似してモデリングする方法を説明します

イメージ図：こういう感じのことをやります

関数でのフィティングは、モデリングの基本です。
線形の近似であれば、普通に線形回帰のパッケージを使えばいいと思いますが、
ここでは非線形関数含め、自分で指定した任意の関数でフィティングする方法を説明します。

使うもの

Pythonのscipyパッケージに入っている、『curve_fit』というモジュールを使います。
より厳密には、scipy.optimize モジュールの一部です。

まず今回使うパッケージを読み込んでおきます。

import.py

##フィッティングに使うもの
from scipy.optimize import curve_fit
import numpy as np

## 図示のために使うもの
import seaborn as sns
import matplotlib.pyplot as plt

numpyは指数関数の表現のために使います。
seabornを使った図示手法に馴染みのない方は、よければこちらをどうぞ

pythonで美しいグラフ描画
http://qiita.com/hik0107/items/3dc541158fceb3156ee0

やり方 − まずは線形関数でやってみる

では実際に関数フィッティングのやり方を見ていきましょう
まず最初に腕ならしのために線形近似をやってみます。

下記のようにして、フィッティングの対象となる観測データを作ります。
線形で近似するので、直線に近い形のものを用意します。

linear.py

list_linear_x = range(0,20,2)

array_error = np.random.normal(size=len(list_linear_x))

array_x = np.array(list_linear_x)
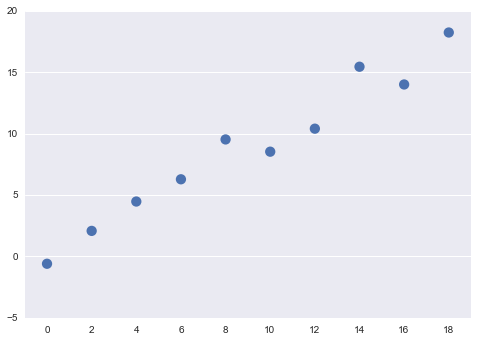
array_y = array_x + array_error ##完全な y=x の直線に誤差項を加えてボコボコしたデータを作ってます

実際に出来上がったデータを見てみます。

linear.py

sns.pointplot(x=array_x, y=array_y, join=False)

※乱数によって多少凸凹具合が違った結果になるので、手元での実行結果とは一致しないと思います。

ではこいつを Y = ax + b の形でフィッティングしてみましょう。
curve_fitの出番です。

fitting.py

## フィッティングしたい関数式を関数として定義してやる
def linear_fit(x, a, b):
    return a*x + b

param, cov = curve_fit(linear_fit, array_x, array_y)

これだけです。第1の返り値paramの中に、リスト形式でパラメータa,bの推定結果が格納されています。
curve_fitの中身は(フィッティングに使う関数,フィッティング対象のx, フィッティング対象のy) で書かれています。なお、第2／第3引数をリスト内包リストで記述すれば、多変数の場合にも対応できます。

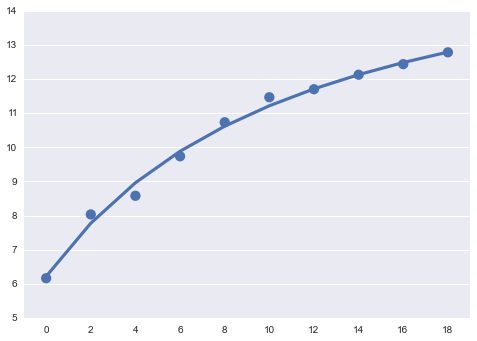
フィッティングの結果を見てみましょう。

fitting.py

array_y_fit = param[0] * array_x + param[1]

sns.pointplot(x=array_x, y=array_y, join=False)
sns.pointplot(x=array_x, y=array_y_fit, markers="")

なお、フィッティングの手法はOLS(最小二乗誤差法)です。

やり方 − 非線形関数でやってみる

次にもう少し複雑な非線形関数での近似をやってみます。
例えば、 f(x) = b * exp( x /(a + x) ) みたいな関数を考えてみましょう。

nonlinear.py

list_y = []

for num in array_x:
    list_y.append( param[1] * np.exp( num /(param[0] + num) ) + np.random.rand() )

array_y= np.array(list_y)
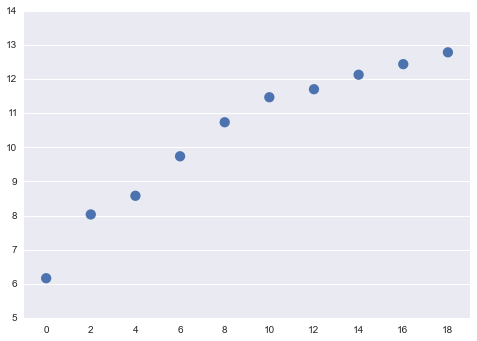
sns.pointplot(x=array_x, y=array_y, join=False)

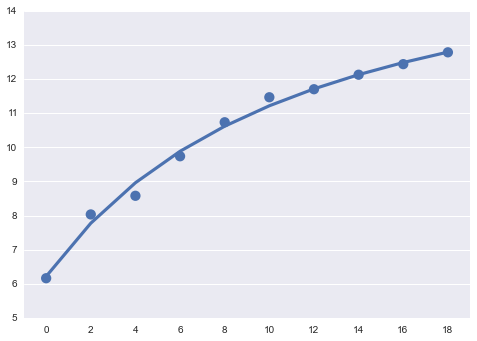
こんな感じのデータを得られました。なんとなく、線形よりも収束するタイプの非線形関数の方がフィットが良さそうです。

ではこいつを f(x) = b * exp( x /(a + x) )の形でフィッティングしてみましょう。

fitting.py

def nonlinear_fit(x,a,b):
    return  b * np.exp(x / (a+x)  )

param, cov = curve_fit(nonlinear_fit, array_x, array_y)

draw.py

list_y = []
for num in array_x:
    list_y.append( param[1] * np.exp( num /(param[0] + num) ))

sns.pointplot(x=array_x, y=array_y, join=False)
sns.pointplot(x=array_x, y=np.array(list_y), markers="")

それっぽくフィッティングできています。

##こちらの記事も
Python Pandasでのデータ操作の初歩まとめ
http://qiita.com/hik0107/items/d991cc44c2d1778bb82e

Pythonでのデータ分析初心者がまず見るべき情報源のまとめ
http://qiita.com/hik0107/items/0bec82cc09d0e05d5357

データサイエンティストに興味があるならまずこの辺りを見ておきな、って文献・動画のまとめ
http://qiita.com/hik0107/items/ef5e044d2f47940ba712