LoginSignup
537
506

More than 5 years have passed since last update.

@masasora

ベイズ最適化入門

Last updated at Posted at 2016-04-02

ベイズ最適化入門

最近ちらほらベイズ最適化について聞くのでまとめてみました。
特に専門でもないので間違ったことが書いてあったりするかもしれませんがもし発見したら指摘して頂けると助かります。

ベイズ最適化のモチベーション

世の中、実際に実験することが面倒くさいものはかなり多いです。なので計画的に実験をデザインしたくなります。
そこで実験するたびに今までの実験結果に基づいて"ベイズ的に"次の実験をデザインするのがベイズ最適化です。
実際使われている分野としては例えば

  • 広告(どのようにA/B testするかとか)
  • 生物学(良さそうなDNAを決定してそれに基づいて実験したいときとか?)
  • 物理or化学（マテリアルデザイン）
  • 機械学習(Deep Learningなど)におけるハイパーパラメータサーチ
  • 強化学習

みたいなものがあるそうです。
最も基本的な例である機械学習のハイパーパラメーターサーチにおいてはマニュアルであったり、自動的にやるとしたらgrid searchやrandomでやるということが多いかと思います。しかしベイズ最適化を使えばもっと上手く行うことができます。
ベイズ最適化では次の実験の結果を予測する代替的な関数(acquisition function)を今までのデータを元に作って、その関数を最大化する点を求め、そこで次の実験を行います。

ベイズ最適化の直感的な説明

強化学習とかでもよく出てくる説明だと思いますが、我々は探索と活用のはざまに揺れています。
活用とはもう既にある程度いいとわかっているものを使うこと、探索とは未知のものに挑戦して全然違う経験を得ることです。
ベイズ最適化とは最適化の枠組みで活用と探索という概念をどちらも考慮して次に選ぶべき行動を選ぶ手法と簡単に言うことができます。つまり活用と探索を考慮したacquisition functionを使うということです。
また人間は何かを買う、何かをはじめてみるなどの状況において無意識的にベイズ最適化を行っているとも言えます。

ベイズ最適化の具体的な説明

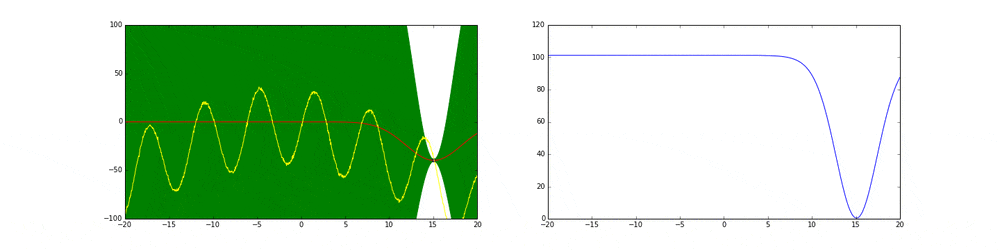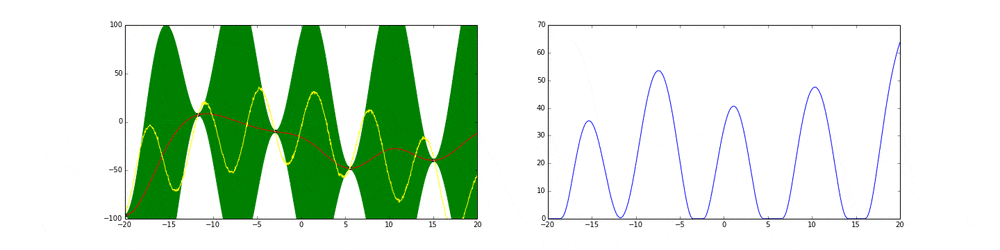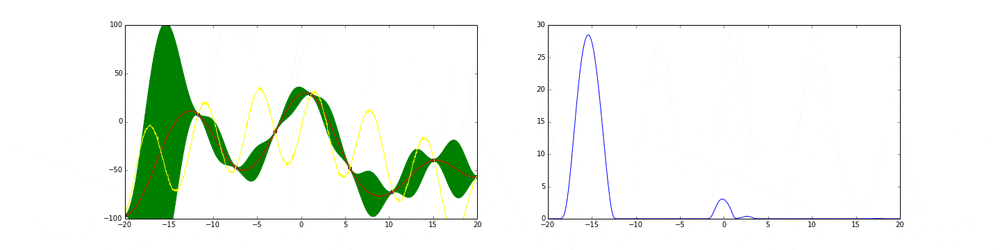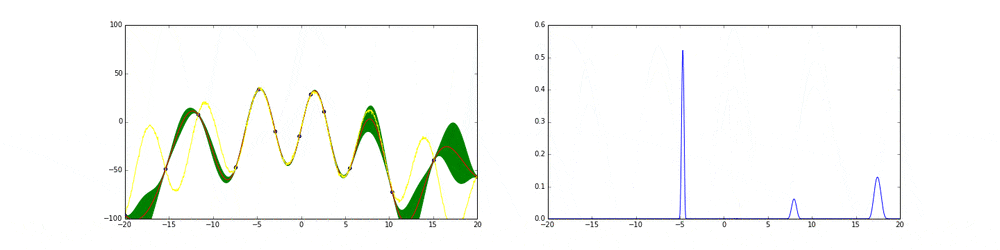
1459589792Q4eF7i9z6oIH0u61459589786.gif

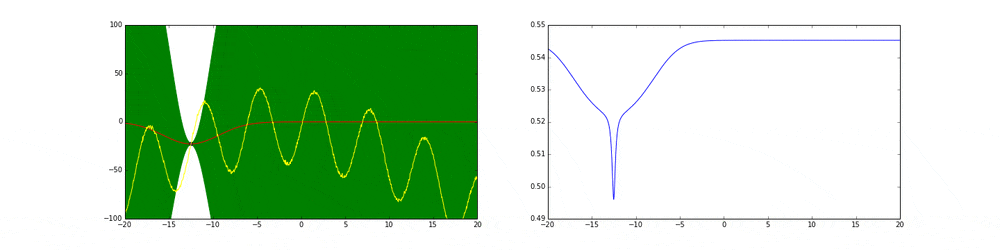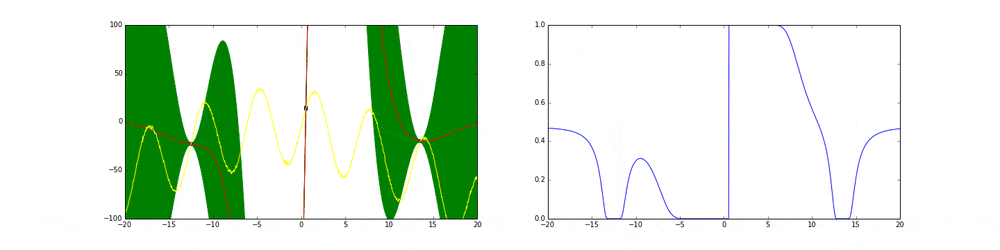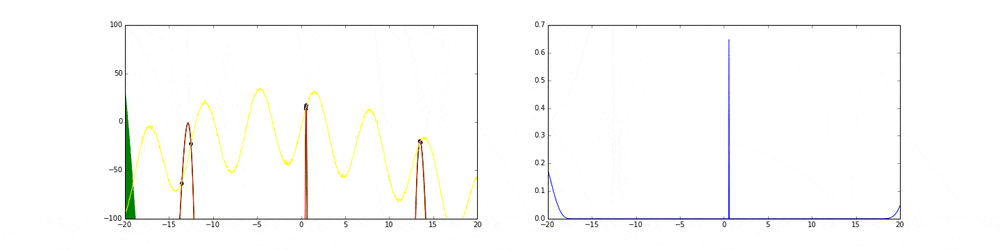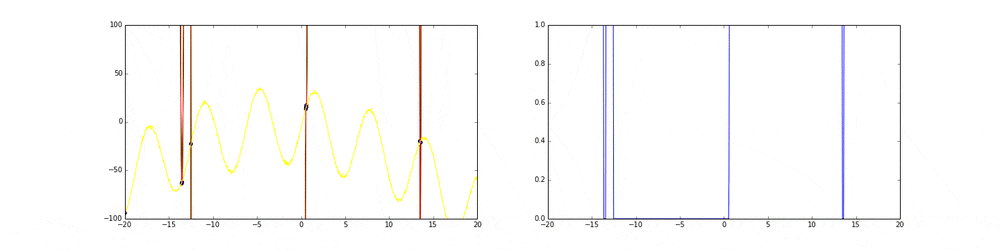
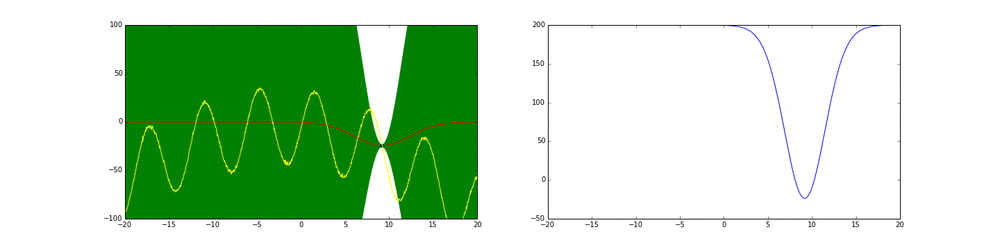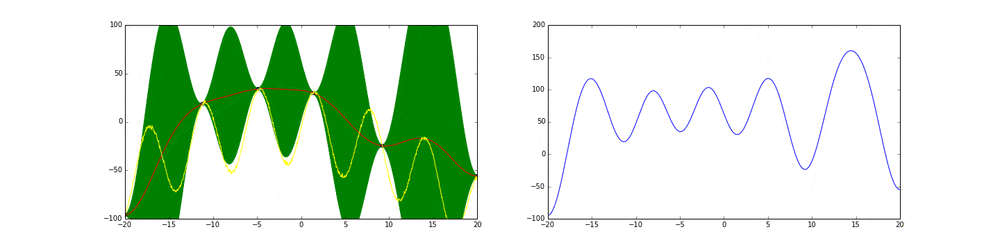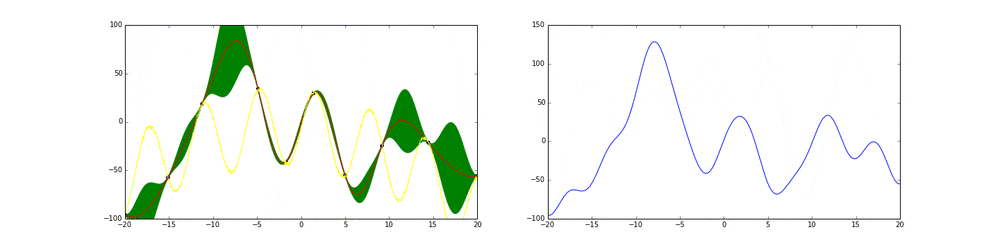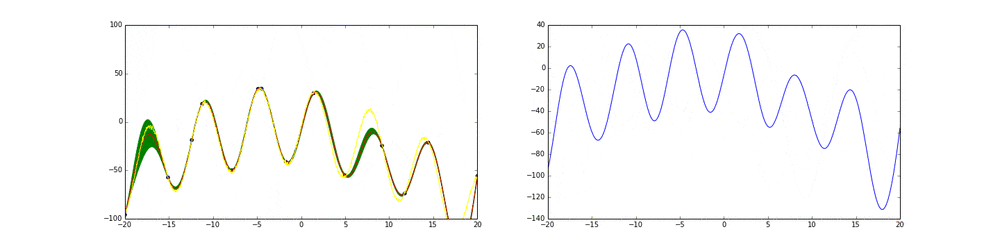
上のgifが大体のベイズ最適化の説明になっています。
まず左にある黄色い線が真の関数です。この関数を最大化する点を求めるためにある制約(今回は(-20,20))の中からうまくだんだん点をとっていこうというのがタスクです。今回は点の評価（実験）は一瞬で終わりますが本来はその評価に時間がかかるということに注意してください。
赤の線は今までのデータ点から予測される予測値の平均値を表しています。緑の領域は信頼区間($平均\pm 分散$)を表しています。この平均と分散は得られたデータ点に基づいてGaussian processを使って算出しています。

点の取り方が問題で点を選ぶ時にベイズ最適化を使います。
まず最初の点はランダムに選ぶとします。次の点からはacquisition functionが高い点を選びます。このacquisition functionは右の青い線で表されています。つまり青い関数において高い点がきっと有望そうだから次はそれにしようということです。
先ほど述べたよう探索と活用を考慮したacquisition functionを作ることがベイズ最適化のキモとも言えます。

ベイズ最適化のもう少し詳しい説明

まずGPについて説明して次にacquisition functionを何種類か紹介します。その後、読んだ文献の中で他に大事そうだったことをまとめました。

Gaussian process(GP)の導入

まず基本的なこととしてGPは確率過程です。確率過程とは確率変数の集合{$X_{t}$}($t \in T$)です。(信号処理において$T$は時間だったりします。機械学習のGPの文脈ではinputの領域です。)

例として$T$が離散的な場合Discrete Markov processがあり、連続的なものの場合Wiener processがあります。確率過程は固定するものを変えることで、時間の関数ともみなせるし、ある時間で切り取ったただの確率変数ともみなせるということはかなり重要です。前者をよくsample pathといいます。
また連続的な確率過程の存在は"consistency"を満たすときに保証されます。　1
Gaussian processではあらゆるxの集合に対するyの同時分布がガウス分布に従います。このとき"consistency"を満たしていることによってそのような連続的な確率過程の存在が保証されます。
またガウス分布は分散と平均が定まれば一意に決定します。平均を0として分散をカーネルとして表現した確率過程が機械学習の文脈で言うガウス過程です。

カーネル回帰の説明

カーネル回帰の一番簡単な解釈はリッジ回帰をカーネルで置き換えたというものですがベイズ最適化の文脈ではあくまで確率過程(gaussian process)としての解釈が重要なのでそちらを書きます。
まず$x$,$y$,$t$があるとします。xは入力、yは出力です。tはyにノイズ(分散が$\beta$)が載ったもので実際の観測値を表します。まずyのpriorを$N(0,K)$(Kはカーネルによるグラム行列)とします。するとN点が観測されたあとの$t_{N+1}$の事後分布(予測分布)が$x_{N+1}$に対して定まります。この事後分布はガウシアンで平均と分散が以下のようになります。

$ \mu_{N+1}= k^{T}(K+\beta I)^{-1}t_{1:N}$ ($k(x_{n},x_{N+1})$を並べたものが$k$)

$ \sigma_{N+1}= k(x_{N+1},x_{N+1})-k^{T}(K+\beta I)^{-1}k$

acquisition functionの設計

上の$x_{N+1}$を選ぶためにacquisition function($a(x)$)を定めます。
前述のとおり活用と探索のトレードオフをうまく汲み取った関数を作ります。”活用”の観点からは平均が高い点を”探索”の観点からは分散が高い点を選べばよいということになります。
これから$f_{+}$はN点目までに得られた点における最大の出力を表すことにします。
一応、コードはここにあげています。
https://github.com/Ma-sa-ue/practice/blob/master/machine%20learning(python)/bayeisan_optimization.ipynb

Probability of Improvement(PI)

1459578637h1DiBeEHdcLl6UW1459578633.gif

$Z = \frac {\mu(x)-f^{+}- \xi}{\sigma(x)},a_{PI}(x)= \Phi (Z)$

$\Phi$は正規分布のcdf。そんなによくないことがgifから分かると思います。$\xi$はgreedyになりすぎることを緩和するため設けていますがそれでも活用に重きが置かれてしまう傾向にあります。

Expected Improvement(EI)

1459589792Q4eF7i9z6oIH0u61459589786.gif

$a_{EI}(x)=(\mu (x)-f_{+}-\xi)\Phi (Z)+\sigma (x)\phi (Z)$

$\phi $は正規分布のpdfです。PIに比べてだいぶよい手法です。improvement ( $f_{N+1}(x)-f^{+}$ )の期待値をとると上のようなります。$\xi$は0.01ぐらいが推奨されているらしいです。

GP Upper (lower) Confidence Band

14595791439NFETVIUPDKiNWu1459579137.gif

$a_{UCB}(x)=\mu (x)+k_{N} \sigma (x)$

これももともとは分散に掛かっている係数は定数となっている単純な手法(Upprt Confidence Bound)です。しかしそれではあんまり上手くいかないので更新ごとに係数を調整しているのがGP-UCBです。EIと同じ傾向を示すことがわかると思います。

Thomson sampling

サンプルパスをとってきてそれをacquisition functionとします。

Information-theoretic approaches

情報理論に基づいた関数を使います。

その他もろもろ

基本的なコンセプトは今まで書かれたことでおそらく終わりだと思うですがこれらのことを踏まえた上で色々な研究がなされています。とりあえず自分が概要を把握している中で上に書いていないけど重要そうなことをまとめてみました。

高次元の探索はどうするの？

探索の入力に対しても多様体仮説が成立する、つまり低次元の部分多様体であるという仮説に基づき低次元に落としつつ最適化を行っていくという手法が提案されています。実際に良い手法らしいです。
http://arxiv.org/pdf/1301.1942.pdf

Input warpningの有効性

普通のカーネルの入れ方だと定常な確率過程を表すことになってしまいます。しかし現実のデータは非定常なことも多いです。
そのような非定常な確率過程を表すために入力を全単射な関数で歪めてやってベイズ最適化を行うというのがアイディアです。
http://jmlr.org/proceedings/papers/v32/snoek14.pdf

そもそもカーネル何選ぶの？

カーネルの選び方はとても重要です。実験では２次形式の指数をとった単純なものを使いましたがベイズ最適化用のカーネルは色々あるらしいです。

カーネルのハイパーパラメータどうするの？

カーネルのハイパーパラメーターの設定をどうするかというのは悩ましい問題です。例えば有名なライブラリのspearmintに使われている手法ではハイパーパラメーターを近似的に積分消去するらしいです。
https://papers.nips.cc/paper/4522-practical-bayesian-optimization-of-machine-learning-algorithms.pdf

ぶっちゃけ単純じゃないですか？

ベイズ最適化自身はかなり昔からあったそうです。それが機械学習の発達につれハイパーパラメーターサーチのためベイズ最適化がまたリバイバルしてきたらしいです。自分の最初の方に書いた程度のことは昔からあったかもしれませんが最近の研究レベルだと理論面でも応用面でも色々発展をとげています。

acquisition functionの最大化どうするの？

注意するべき点としてベイズ最適化は目的関数の観測が面倒という前提でやっています。動画の$y$はすぐ得られていますがもちろん実際はそんなすぐに得られないという訳です。一方、acquisition functionの評価は簡単です。でも凸とか微分可能という保障はないので区間を分割して最大値を求めるとか原始的な手法だったりを使います。(たぶん)

目的関数の観測にかかるコストってそれぞれの入力によって違うのでは？

観測のコストはそれなりにかかるという前提ですがそれでも入力によってコストが違うのも事実です。それを考慮したモデルもあるそうです。

参考文献(正直、この記事を読むよりこっち読んだほうがためになります)

  1. marginalizeしたとき整合性を満たせばいいという分かりやすい主張ですが証明はかなり複雑です。Kolmogorovによって証明されています。連続時間上の確率過程を厳密に議論してくのは相当骨が折れます。 ↩

537
506
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
537
506