はじめに
本記事は、下記のハイパーパラメータチューニングに関する記事の、XGBoostにおける実装例を紹介する記事となります。
XGBoostとパラメータチューニング
XGBoostは分類や回帰に用いられる機械学習アルゴリズムで、その性能の高さや使い勝手の良さ(特徴量重要度などが出せる)から、特に回帰においてはLightBGMと並ぶメジャーなアルゴリズムです。
一方でXGBoostは多くのハイパーパラメータを持つため、その性能を十分に発揮するためにはパラメータチューニングが重要となります。
チューニング対象のパラメータ
XGBoostの主なパラメータは、こちらの記事で分かりやすく解説されています。
XGBoostのパラメータ数は他の回帰アルゴリズム(例:ラッソ回帰(1種類)、SVR(3種類))と比べてパラメータの数が多く、また使用するboosterやAPI(Scikit-learn API or Learning API)によってパラメータの数が変わるなど、複雑なパラメータ構成を持っています。
そのため、全てのパラメータをチューニング対象とすると制御が難しく、一部の重要なパラメータのみを選んでチューニング対象とすることが一般的です。
本記事で使用するパラメータ
本記事では、Optuna公式サンプルコードのチューニング対象パラメータを使用します。
またチューニングに先立ち、学習に使用するAPIおよび使用するboosterを選択する必要があります。今回は
| 選択内容 | 選択する方式 | 選択理由 |
|---|---|---|
| API | Scikit-Learn API | Scikit-Learnの各種チューニング用メソッドを利用するため |
| booster | gbtree | 最もよく使われる方式 |
を採用します
この際、Scikit-learn APIとLearning APIで一部パラメータの名称が異なるのでご注意ください
今回使用するパラメータ一覧と、対応する名称を下記に列記します
| Scikit-Learn APIでの名称 |
Learning APIでの 名称 |
型 (スケール) | 範囲 | デフォルト値 | 内容 |
|---|---|---|---|---|---|
| subsample | subsample | float (linear) | 0-1 | 1.0 | 各決定木においてランダムに抽出される標本の割合(大きいほど過学習寄り) |
| colsample _bytree | colsample _bytree | float (linear) | 0-1 | 1.0 | 各決定木においてランダムに抽出される列の割合 |
| reg_alpha | alpha | float (log) | 0-∞ | 0 | 決定木の葉の重みに関するL1正則化項(小さいほど過学習寄り) |
| reg_lambda | lambda | float (log) | 0-∞ | 1 | 決定木の葉の重みに関するL2正則化項(小さいほど過学習寄り) |
| learning_rate | eta | float (log) | 0-∞ | 0.3 | 過学習防止のための学習率パラメータ(大きいほど過学習寄り) |
| min_child _weight | min_child _weight | float (linear) | 0-∞ | 1 | 決定木の葉の重みの下限(小さいほど過学習寄り) |
| max_depth | max_depth | int (linear) | 0-∞ | 6 | 決定木の深さの最大値(大きいほど過学習寄り) |
| gamma | gamma | float (log) | 0-∞ | 0 | 決定木の葉の追加による損失減少の下限(小さいほど過学習寄り) |
実装
下図のフロー(こちらの記事と同じ)に基づき、XGBoost回帰におけるチューニングを実装します
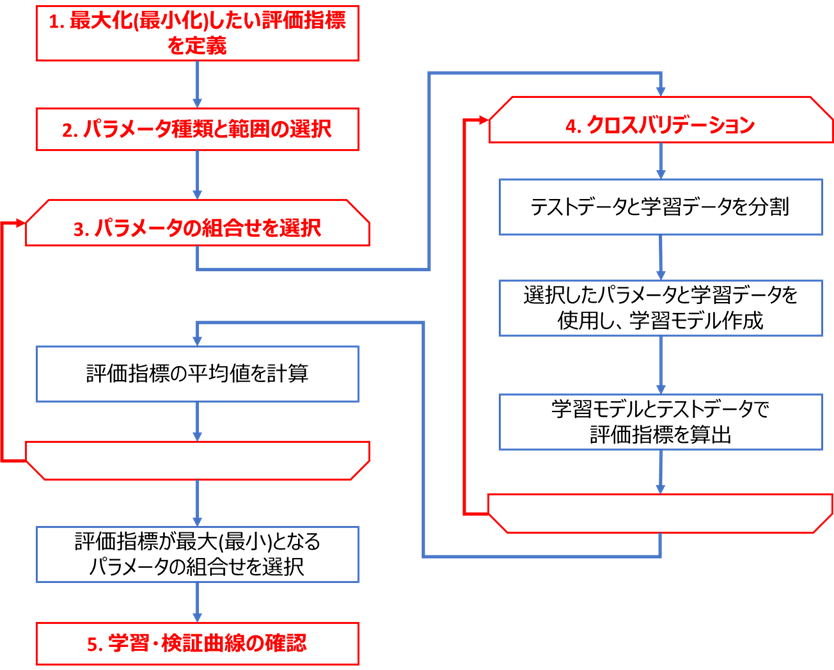
コードはこちらのGitHub(xgb_tuning_tutorials.py)にもアップロードしております。
実装に必要な環境整備
ライブラリ
チューニングの実装に必要なライブラリ等をインストールします。
私の環境では、以下のライブラリを使用しています
・Python本体 (動作確認時は3.9.5を使用)
・Matplotlibで表示可能な環境 (Jupyter等)
・下記ライブラリ (参考として動作確認時のライブラリバージョンも記載)
xgboost (1.4.2)
scikit-learn (0.24.2)
bayesian-optimization (1.2.0)
optuna (2.7.0)
numpy (1.20.3)
pandas (1.2.4)
seaborn (0.11.0)
matplotlib (3.4.2)
・こちらの回帰可視化ライブラリ(チューニング前後のモデル可視化にのみ使用するので、なくともチューニング自体はできます)
使用するサンプルデータ
こちらの記事の、大阪都構想選挙データを使用します
ハードウェア
チューニング速度はCPU等の性能に大きく依存します
参考までに本記事で使用したPC(Lenovoのモバイル)のスペックを下記します
| デバイス | スペック |
|---|---|
| CPU | Intel Core i5-8250U@1.6GHz |
| メモリ | 8GB(4+4) DDR4 2400MHz SODIMM |
| ストレージ | SSD PCIe M.2 |
| OS | Windows 10 Pro 64bit |
コードの実行にはVSCodeのJupyter拡張を使用しております。
CPUやメモリの使用状況にもチューニングは左右されますが、余計なプロセスを終了してからチューニングを開始することで、繰り返してもほぼ同じ所要時間となり、再現性のとれる結果となりました。
実際の実装例
前述のフローに基づき実装を進めていきます
データの読込
こちらのデータセットをCSVからPandasのDataFrame(Jupyterでの表示用)およびNumpyのndarray(XGBoostモデルへの読込用)に読み込みます
import pandas as pd
import time
df_osaka = pd.read_csv(f'./sample_data/osaka_metropolis_english.csv')
OBJECTIVE_VARIALBLE = 'approval_rate' # 目的変数
USE_EXPLANATORY = ['2_between_30to60', '3_male_ratio', '5_household_member', 'latitude'] # 説明変数
y = df_osaka[OBJECTIVE_VARIALBLE].values # 目的変数をndarray化
X = df_osaka[USE_EXPLANATORY].values # 説明変数をndarray化
# データを表示
df_osaka[USE_EXPLANATORY + [OBJECTIVE_VARIALBLE]]
2_between_30to60 3_male_ratio 5_household_member latitude approval_rate
0 0.499141 0.485807 1.83 42.325 0.562728
1 0.425080 0.481006 2.10 42.078 0.526104
2 0.467986 0.473394 2.06 41.535 0.536686
3 0.411267 0.473798 2.20 40.197 0.496048
4 0.390663 0.473722 2.16 43.273 0.471734
5 0.419868 0.474112 2.25 42.190 0.504592
6 0.422815 0.475847 2.52 42.257 0.511019
7 0.342897 0.577474 1.75 38.090 0.492851
8 0.506583 0.468446 1.65 40.870 0.509798
9 0.496780 0.467432 1.96 40.575 0.538094
10 0.374845 0.486567 2.34 39.018 0.465384
11 0.462086 0.505250 1.61 39.560 0.516693
12 0.383394 0.478802 2.36 36.575 0.486810
13 0.392461 0.465524 2.15 36.222 0.450049
14 0.390136 0.471774 2.38 37.270 0.456477
15 0.450164 0.464464 2.06 39.467 0.478386
16 0.368153 0.480087 2.27 39.218 0.480658
17 0.409648 0.460738 2.22 38.316 0.450814
18 0.386937 0.469701 2.23 37.322 0.473037
19 0.402482 0.488469 2.29 40.980 0.468385
20 0.400149 0.486460 2.18 39.835 0.429843
21 0.406196 0.490601 2.35 42.683 0.473805
22 0.433488 0.496974 1.97 43.260 0.550678
23 0.409827 0.491403 1.99 44.470 0.502997
チューニング前のモデルの確認
こちらのライブラリで、チューニング前モデルの特徴量と目的変数の関係を可視化します
from seaborn_analyzer import regplot
from xgboost import XGBRegressor
from sklearn.model_selection import KFold
# 乱数シード
seed = 42
# モデル作成
model = XGBRegressor(booster='gbtree', objective='reg:squarederror',
random_state=seed, n_estimators=10000) # チューニング前のモデル
# 学習時fitパラメータ指定
fit_params = {'verbose': 0, # 学習中のコマンドライン出力
'early_stopping_rounds': 10, # 学習時、評価指標がこの回数連続で改善しなくなった時点でストップ
'eval_metric': 'rmse', # early_stopping_roundsの評価指標
'eval_set': [(X, y)] # early_stopping_roundsの評価指標算出用データ
}
# クロスバリデーションして決定境界を可視化
seed = 42 # 乱数シード
cv = KFold(n_splits=3, shuffle=True, random_state=seed) # KFoldでクロスバリデーション分割指定
regplot.regression_heat_plot(model, USE_EXPLANATORY, OBJECTIVE_VARIALBLE, df_osaka,
pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
cv=cv, display_cv_indices=0,
fit_params=fit_params)
男性比率(3_male_ratio)が高いほど、30-60代(2_between_30to60)が多いほど、北に(latitude)行くほど賛成率(approval_rate)が高い=色が濃いことが分かり、チューニング前でもある程度傾向が捉えられていることが分かります。
XGBRegressorはScikit-Learn APIにおけるXGBoost回帰を実行するクラスで、objectiveが学習時に使用する評価指標、random_stateが使用する乱数シードです。
・early_stopping_roundsについて
XGBoostにはearly_stopping_roundsという便利な機能があります。
XGBoostやLightGBMは学習を繰り返すことで性能を上げていくアルゴリズムですが、学習回数を増やしすぎると性能向上が止まって横ばいとなり、無意味な学習を繰り返して学習時間増加の原因となってしまいます(参考)
early_stopping_roundsは、この学習回数を適切なタイミングで打ち止めるための仕組みで、 「○回連続で評価指標が向上しなくなったら、学習を打ち止める」 というアルゴリズムとなっています。
後述の計算打ち切り問題もあるので、基本的にはearly_stopping_roundsを指定した方が良い かと思います。
Scikit-Learn APIのXGBoostでearly_stopping_roundsを利用する場合、fit_params引数にdict形式で'early_stopping_rounds'、'eval_metric'および'eval_set'を指定します。
また、連続条件に至る前に学習が打ち切られないよう、n_estimatorsに大きな値(例:10000)を指定する必要もあります。
| fit_paramsの引数名 | 意味 |
|---|---|
| early_stopping_rounds | 上記の「○回連続」を指定する引数 |
| eval_metric | 「評価指標」 |
| eval_set | 上記「評価指標」算出のためのデータセットを指定する引数 |
| (verbose) | 学習中のコマンドライン出力(0から2に大きくなるにつれ経過表示が細かくなる) |
eval_setは本来であれば検証用データを入れる事が望ましいですが、cross_val_scoreメソッドの外側で検証用データを分けることができないので、本記事ではCV分割前のデータをそのまま入力します。
(厳密性にこだわる方は、cross_val_scoreやGridSearchCVクラスを使わず、スクラッチでクロスバリデーションを実装してください)
(参考記事でもtest_loglossが収束するタイミングとeval_loglossが収束するタイミングに大きな差はなく、私の経験上からもどちらのデータをeval_setに入れてもスコアに大きな差はないので、実用上は問題がないと考えています)
またeval_metricおよび前述のobjectiveは、後述の「手順1」で指定する評価指標に合わせることが望ましいです。
| 評価指標の名称 | 手順1の評価指標 | objective | eval_metric |
|---|---|---|---|
| RMSE | 'neg_mean_squared_error' | 'reg:squarederror' | 'rmse' |
| RMSLE | 'neg_mean_squared_log_error' | 'reg:squaredlogerror' | 'rmsle' |
| MAE | 'neg_mean_absolute_error' | 'reg:pseudohubererror' | 'mae' |
※'reg:pseudohubererror'は、厳密にはMAEと異なりますが、微分不可能なMAEを2階微分できるように改良した指標だそうです(公式に記載、こちらも参照)
参考までに、分類での評価指標も列記します
(APIドキュメントを見る限りobjective(学習時の評価指標)は2値分類時はbinary:logistic(、ロジスティック回帰)を使用するのが基本となりそうです。手順1の評価指標とeval_metricはAUCなども選択できます。詳しくはリンクを参照ください)
| 評価指標の名称 | 手順1の評価指標 | objective | eval_metric |
|---|---|---|---|
| LogLoss (2値分類) | 'neg_log_loss' | 'binary:logistic' | 'logloss' |
| LogLoss (多クラス分類) | 'neg_log_loss' | 'multi:softmax' | 'mlogloss' |
| AUC(2クラス分類) | 'roc_auc' | 'binary:logistic' | 'auc' |
| AUC(多クラス分類) | 'roc_auc_ovr' | 'multi:softprob' | 'auc' |
| PR-AUC(2クラス分類のみ) | 'average_precision' | 'binary:logistic' | 'aucpr' |
手順1 最大化したい評価指標の定義
今回は
・回帰
・外れ値が多いデータではない
ので、こちらのフローに基づきRMSE(Scikit-Learnでは'neg_mean_squared_error')を採用します。
チューニング前の評価指標をクロスバリデーションで算出します。
# %% 手順1) チューニング前の評価指標算出
from sklearn.model_selection import cross_val_score
import numpy as np
X = df_osaka[USE_EXPLANATORY].values
y = df_osaka[OBJECTIVE_VARIALBLE] # 目的変数をndarray化
scoring = 'neg_mean_squared_error' # 評価指標をRMSEに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, n_jobs=-1, fit_params=fit_params)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
scores=[-0.00074938 -0.0006097 -0.00045056]
average_score=-0.0006032139207020372
チューニング前のスコア(neg_mean_squared_error = -MSE)は-0.000603であることが分かりました。
チューニングでこの値を改善していきます
手順2 パラメータ種類と範囲の選択
・種類
Optunaサンプルコードに基づき、前述の8パラメータを使用します
・範囲
適当な初期範囲を定めて検証曲線をプロットし、その結果に基づいて範囲を調整していきます。
from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
cv_params = {'subsample': [0, 0.1, 0.2, 0.3, 0.4, 0.6, 0.7, 0.8, 0.9, 1.0],
'colsample_bytree': [0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'reg_alpha': [0, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1.0],
'reg_lambda': [0, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1.0],
'learning_rate': [0, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1.0],
'min_child_weight': [1, 3, 5, 7, 9, 11, 13, 15],
'max_depth': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
'gamma': [0, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 1.0]
}
param_scales = {'subsample': 'linear',
'colsample_bytree': 'linear',
'reg_alpha': 'log',
'reg_lambda': 'log',
'learning_rate': 'log',
'min_child_weight': 'linear',
'max_depth': 'linear',
'gamma': 'log'
}
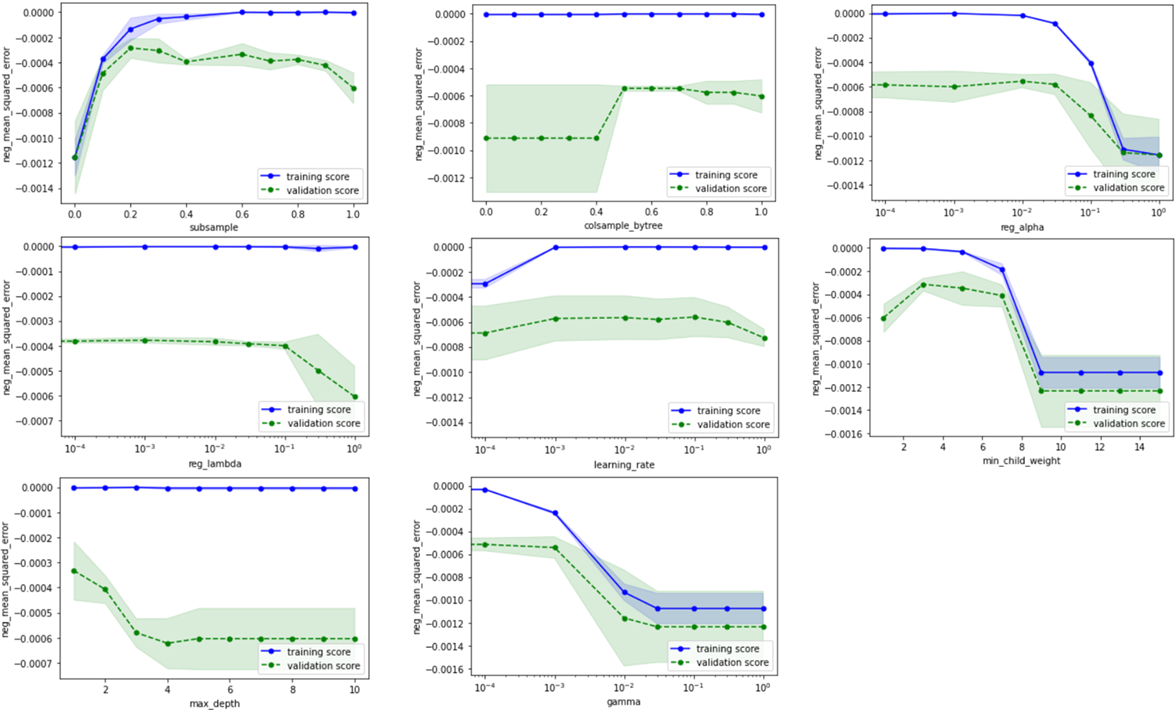
# 検証曲線のプロット(パラメータ毎にプロット)
for i, (k, v) in enumerate(cv_params.items()):
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
fit_params=fit_params,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# スケールをparam_scalesに合わせて変更
plt.xscale(param_scales[k])
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
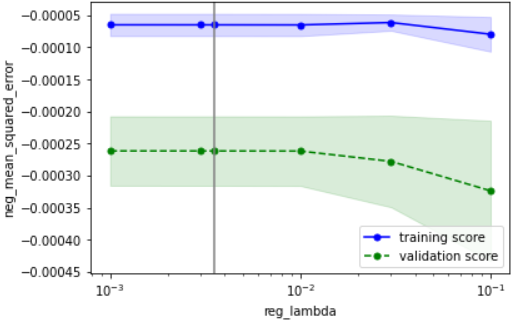
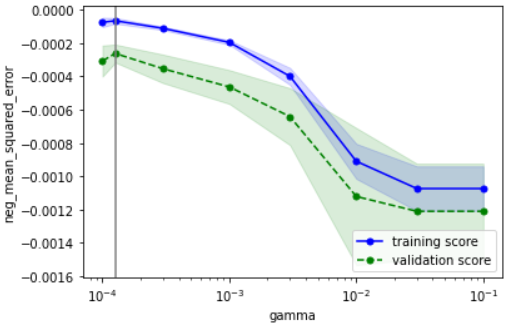
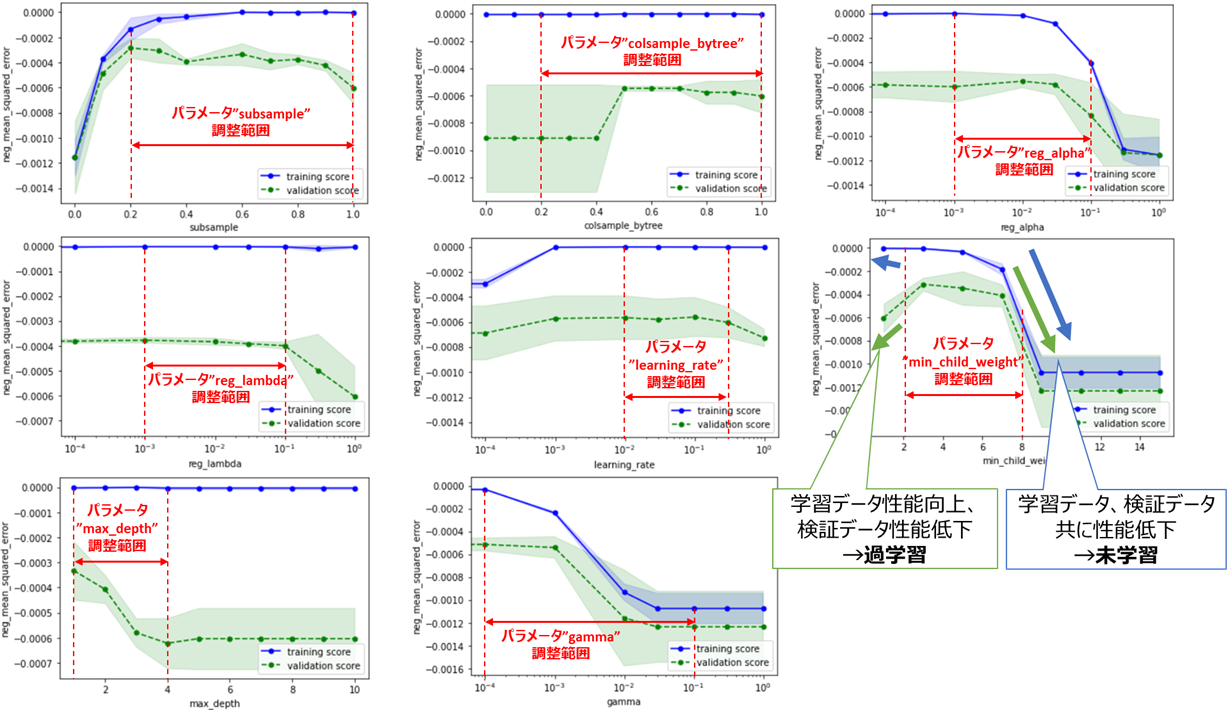
SVMのときほど顕著な傾向は出ていませんが、過学習または未学習になり過ぎない範囲を基準に、以下のようにチューニング範囲を定めます
手順3&4 パラメータ選択&クロスバリデーション
SVMのときと同様に、下記A、B、C (BayesianOptimization)、C (Optuna)の4種類の実装法をそれぞれ解説します。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | **グリッドサーチ ** | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
また、SVMと比べXGBoostは処理が重いため、チューニング時間が課題となります。
スコアと共にチューニングにかかった時間も測定し、各アルゴリズムで比較してみます。
処理時間は試行数にも依存するため、後述のearly_stopping_roundなしのとき(=パラメータによる学習の収束速度に左右されない)のチューニング時間が等しくなる、という基準で、各アルゴリズムの試行数を定めました
| 名称 | 試行数 | early_stopping_roundなし時のチューニング所要時間 |
|---|---|---|
| **グリッドサーチ ** | 1024 (4パラメータ^5) |
186秒 |
| ランダムサーチ | 1000 | 177秒 |
| ベイズ最適化 (Bayesian Optimization) |
250 (初期20+ベイズ230) |
180秒 |
| ベイズ最適化 (Optuna) |
600 | 162秒 |
グリッドサーチの場合
GridSearchCVクラスで、グリッドサーチによる最適化を実行します。
グリッドサーチで8種類のパラメータ全てをチューニングすると、3段階に絞っても3^8 = 6561回の試行が必要となり、処理時間が掛かりすぎてしまうため、
今回は特に重要な5パラメータに絞ってチューニングします。
(5パラメータそれぞれ4段階のチューニング範囲を設定し、4^5 = 1024回の試行)
from sklearn.model_selection import GridSearchCV
start = time.time()
# 最終的なパラメータ範囲
cv_params = {'learning_rate': [0.01, 0.03, 0.1, 0.3],
'min_child_weight': [2, 4, 6, 8],
'max_depth': [1, 2, 3, 4],
'colsample_bytree': [0.2, 0.5, 0.8, 1.0],
'subsample': [0.2, 0.5, 0.8, 1.0]
}
# グリッドサーチのインスタンス作成
gridcv = GridSearchCV(model, cv_params, cv=cv,
scoring=scoring, n_jobs=-1)
# グリッドサーチ実行(学習実行)
gridcv.fit(X, y, **fit_params)
# 最適パラメータの表示と保持
best_params = gridcv.best_params_
best_score = gridcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'colsample_bytree': 1.0, 'learning_rate': 0.3, 'max_depth': 1, 'min_child_weight': 4, 'subsample': 0.8}
スコア -0.0002767765637463618
所要時間571.768007516861秒
colsample_bytree=1.0
learning_rate=0.3
max_depth=1
min_child_weight=4
subsample=0.8
のときに評価指標neg_mean_squared_errorが最大となり、 その時の評価指標は-0.00276‥ であることが分かります
パラメータの値と学習速度について
上記を見ると、後述のearly_stopping_roundを設定しないときと比べて所要時間が倍以上に増えていますが、自作ライブラリ(後日公開&記事化します)でパラメータと所要時間の関係を測定したところ、下図のようにlearning_rateが小さいとき&subsampleが大きいときに学習時間が指数関数的に増える(収束速度が遅くなる)ことが分かりました。
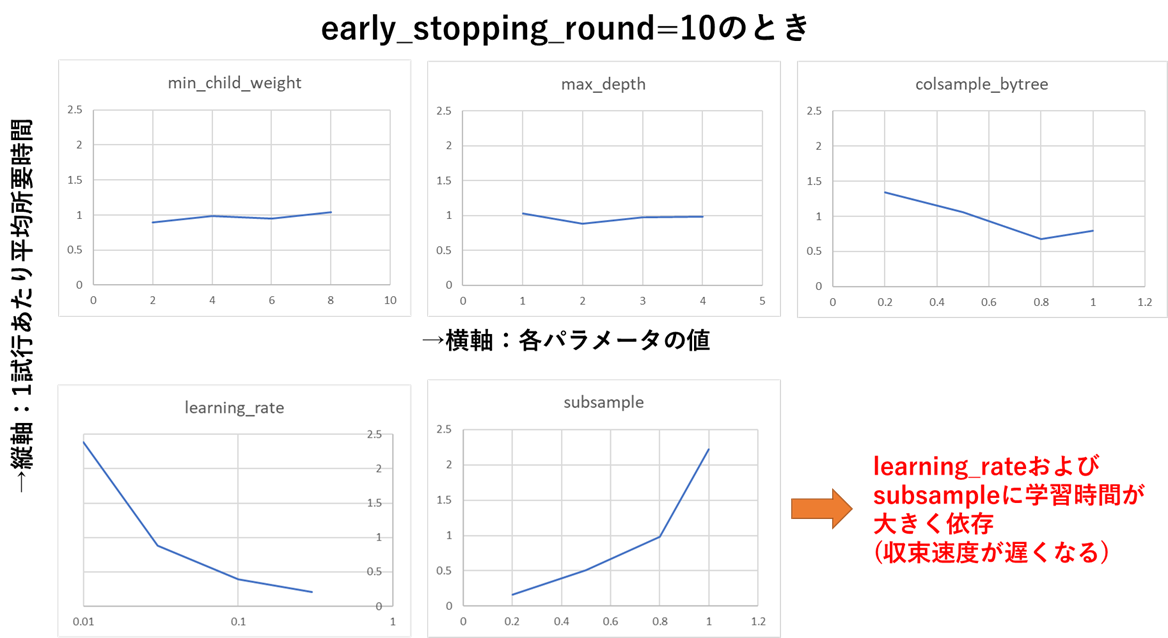
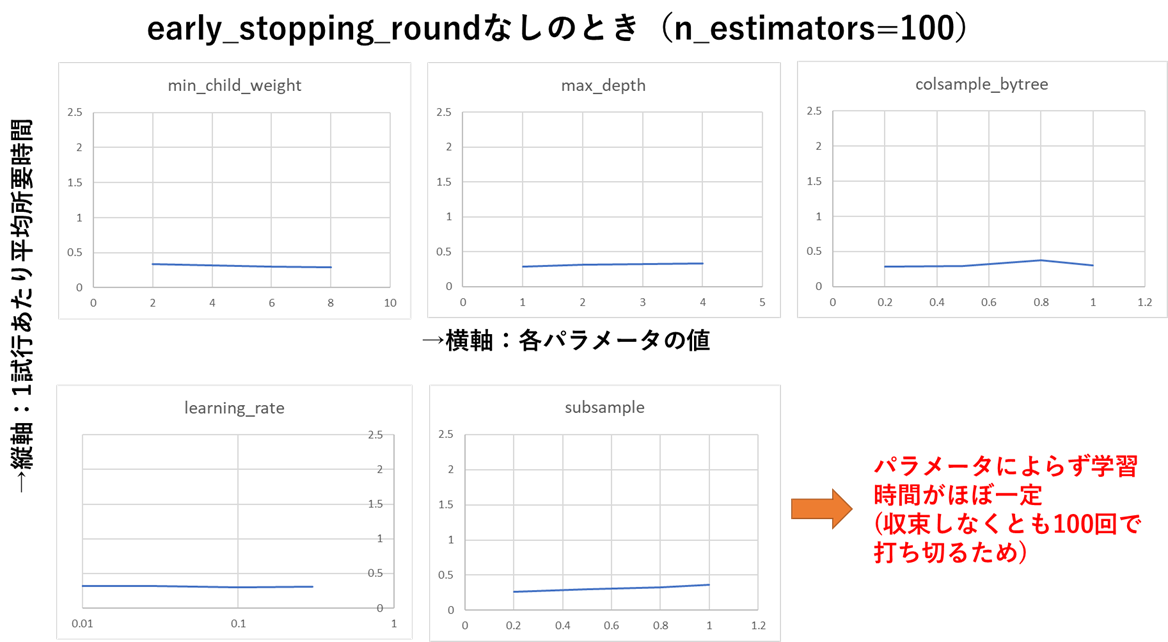
early_stopping_roundを指定しなければこの速度低下が防げるように見えますが、この場合は収束していないのに学習を打ち切っているため、学習性能ををフルに発揮できていないという意味で、やはり避けるべき状況です。
グリッドサーチはチューニング範囲の端部もしっかり学習対象とするため、XGBoostのように指数関数的に学習時間を増やすパラメータをチューニング対象とする場合、グリッドサーチは学習時間で不利となることが分かりました。
グリッドサーチ以外でも、チューニング時間短縮には一部のパラメータの範囲を狭める (learning_rateの下限を大きく、subsampleの上限を小さく)ことが有効と言えるかと思います。
ランダムサーチの場合
RondomizedSearchCVクラスで、ランダムサーチによる最適化を実行します
from sklearn.model_selection import RandomizedSearchCV
start = time.time()
# パラメータの種類と密度をグリッドサーチのときより増やす
cv_params = {'learning_rate': [0.01, 0.02, 0.05, 0.1, 0.2, 0.3],
'min_child_weight': [2, 3, 4, 5, 6, 7, 8],
'max_depth': [1, 2, 3, 4],
'colsample_bytree': [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample': [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'reg_alpha': [0.001, 0.003, 0.01, 0.03, 0.1],
'reg_lambda': [0.001, 0.003, 0.01, 0.03, 0.1],
'gamma': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1]
}
# ランダムサーチのインスタンス作成
randcv = RandomizedSearchCV(model, cv_params, cv=cv,
scoring=scoring, random_state=seed,
n_iter=1000, n_jobs=-1)
# ランダムサーチ実行(学習実行)
randcv.fit(X, y, **fit_params)
# 最適パラメータの表示と保持
best_params = randcv.best_params_
best_score = randcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'subsample': 0.9, 'reg_lambda': 0.03, 'reg_alpha': 0.003, 'min_child_weight': 5, 'max_depth': 1, 'learning_rate': 0.3, 'gamma': 0.0001, 'colsample_bytree': 0.6}
スコア -0.00031207577460643285
所要時間193.16713666915894秒
colsample_bytree=0.9
learning_rate=0.3
max_depth=1
min_child_weight=5
subsample=0.9
reg_lambda=0.03
reg_alpha=0.003
gamma=0.0001
のときに評価指標neg_mean_squared_errorが最大となり、その時の 評価指標は-0.00312‥ (グリッドサーチのときより少し悪い)であることが分かります
また、ランダムサーチはsubsampleやlearning_rateがチューニング範囲の端部をとる(=学習時間が急増する)組合せが少ないので、グリッドサーチのときほどチューニング時間の増加は起こっていません。
ベイズ最適化(BayesianOptimization)の場合
BayesianOptimizationによるベイズ最適化の実装法を解説します。
3.1の教訓に基づき、今回は最初から対数スケールに対応した実装法を採用します
from bayes_opt import BayesianOptimization
start = time.time()
# パラメータ範囲(Tupleで範囲選択)
bayes_params = {'learning_rate': (0.01, 0.3),
'min_child_weight': (2, 8),
'max_depth': (1, 4),
'colsample_bytree': (0.2, 1.0),
'subsample': (0.2, 1.0),
'reg_alpha': (0.001, 0.1),
'reg_lambda': (0.001, 0.1),
'gamma': (0.0001, 0.1)
}
# 対数スケールパラメータを対数化
param_scales = {'learning_rate': 'log',
'min_child_weight': 'linear',
'max_depth': 'linear',
'colsample_bytree': 'linear',
'subsample': 'linear',
'reg_alpha': 'log',
'reg_lambda': 'log',
'gamma': 'log'
}
bayes_params_log = {k: (np.log10(v[0]), np.log10(v[1])) if param_scales[k] == 'log' else v for k, v in bayes_params.items()}
# 整数型パラメータを指定
int_params = ['min_child_weight', 'max_depth']
# ベイズ最適化時の評価指標算出メソッド(引数が多いので**kwargsで一括読込)
def bayes_evaluate(**kwargs):
params = kwargs
# 対数スケールパラメータは10のべき乗をとる
params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in params.items()}
# 整数型パラメータを整数化
params = {k: round(v) if k in int_params else v for k, v in params.items()}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, fit_params=fit_params, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params_log, random_state=seed)
bo.maximize(init_points=20, n_iter=230, acq='ei')
# 最適パラメータとスコアを取得
best_params = bo.max['params']
best_score = bo.max['target']
# 対数スケールパラメータは10のべき乗をとる
best_params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in best_params.items()}
# 整数型パラメータを整数化
best_params = {k: round(v) if k in int_params else v for k, v in best_params.items()}
# 最適パラメータを表示
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
※bo.maximizeの引数init_points, n_iter, acqは、こちらを参考に適宜変更してください
最適パラメータ {'colsample_bytree': 0.5209427700104388, 'gamma': 0.00011232183185766048, 'learning_rate': 0.19648678476501713, 'max_depth': 2, 'min_child_weight': 3, 'reg_alpha': 0.0026548907196842636, 'reg_lambda': 0.006505737123272226, 'subsample': 0.7705550715893523}
スコア -0.0002846640557647852
所要時間200.40562987327576秒
colsample_bytree=0.521
learning_rate=0.196
max_depth=2
min_child_weight=3
subsample=0.771
reg_lambda=0.00651
reg_alpha=0.00265
gamma=0.000112
のときに評価指標neg_mean_squared_errorが最大となり、その時の 評価指標は-0.00284‥ であることが分かります。
評価指標はグリッドサーチとほぼ同等、速度はランダムサーチとほぼ同等と、良好な結果です
ベイズ最適化(Optuna)の場合
Optunaによるベイズ最適化の実装法を解説します。
import optuna
start = time.time()
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
params = {
'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.3, log=True),
'min_child_weight': trial.suggest_int('min_child_weight', 2, 8),
'max_depth': trial.suggest_int('max_depth', 1, 4),
'colsample_bytree': trial.suggest_float('colsample_bytree', 0.2, 1.0),
'subsample': trial.suggest_float('subsample', 0.2, 1.0),
'reg_alpha': trial.suggest_float('reg_alpha', 0.001, 0.1, log=True),
'reg_lambda': trial.suggest_float('reg_lambda', 0.001, 0.1, log=True),
'gamma': trial.suggest_float('gamma', 0.0001, 0.1, log=True),
}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, fit_params=fit_params, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
study = optuna.create_study(direction='maximize',
sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=600)
# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')
最適パラメータ {'learning_rate': 0.1504679873772579, 'min_child_weight': 3, 'max_depth': 2, 'colsample_bytree': 0.9111300404192453, 'subsample': 0.5714914005248717, 'reg_alpha': 0.002208372772109105, 'reg_lambda': 0.0035268968956977302, 'gamma': 0.00012640502817271783}
スコア -0.00026170546747993165
所要時間188.8140163421631秒
colsample_bytree=0.911
learning_rate=0.150
max_depth=2
min_child_weight=3
subsample=0.571
reg_lambda=0.00352
reg_alpha=0.00221
gamma=0.000126
のときに評価指標neg_mean_squared_errorが最大となり、その時の 評価指標は-0.00261‥ であることが分かります。
以上、4種類のアルゴリズムでのチューニング結果をまとめると、下の表のようになります。
| 名称 | スコア(大きいほどGood) | 所要時間 |
|---|---|---|
| グリッドサーチ | -0.000277 | 572秒 |
| ランダムサーチ | -0.000312 | 193秒 |
| ベイズ最適化 (Bayesian Optimization) |
-0.000285 | 200秒 |
| ベイズ最適化 (Optuna) |
-0.000262 | 189秒 |
Optunaが速度、評価指標共にトップであり、効率良い探索ができていることが分かります。
※参考:early_stopping_round不使用時のチューニング結果
上記のパターンではグリッドサーチが多くの時間が掛かっていますが、early_stopping_roundを指定しない場合(常にデフォルトの学習回数100回を使用)では、他のアルゴリズムとほぼ同時間で処理が完了できます(前述の収束前に学習が終了する問題はありますが‥)
参考までに、early_stopping_roundを指定しない場合のスコアと所要時間を下記します
最適パラメータ {'colsample_bytree': 0.5, 'learning_rate': 0.3, 'max_depth': 1, 'min_child_weight': 2, 'subsample': 0.2}
スコア -0.0002765239867990543
所要時間185.77766609191895秒
最適パラメータ {'subsample': 0.9, 'reg_lambda': 0.03, 'reg_alpha': 0.003, 'min_child_weight': 5, 'max_depth': 1, 'learning_rate': 0.3, 'gamma': 0.0001, 'colsample_bytree': 0.6}
スコア -0.00032183034499993064
所要時間177.42294645309448秒
最適パラメータ {'colsample_bytree': 0.6395930243632622, 'gamma': 0.000180988607535196, 'learning_rate': 0.2172024997479354, 'max_depth': 1, 'min_child_weight': 3, 'reg_alpha': 0.0015384076347391687, 'reg_lambda': 0.08556384133211373, 'subsample': 0.6215702870687078}
スコア -0.0002755687009534284
所要時間179.81448650360107秒
最適パラメータ {'learning_rate': 0.2974180333565237, 'min_child_weight': 3, 'max_depth': 1, 'colsample_bytree': 0.6677700394101656, 'subsample': 0.5770218542438953, 'reg_alpha': 0.0014363295487841035, 'reg_lambda': 0.0011632103196598247, 'gamma': 0.00018390932210525767}
スコア -0.00020318715000888437
所要時間161.67626357078552秒
いずれにせよ、Optunaが最も効率よくチューニングできていることが分かります。Optunaの性能恐るべしですね!
手順5 学習・検証曲線の確認
学習、検証曲線で過学習の有無を確認します。
今回はOptunaで調整したパラメータ(colsample_bytree=0.911‥, learning_rate=0.150‥)を例に描画してみます。
学習曲線
学習曲線をプロットし、
・目標性能を達成しているか
・過学習していないか
を確認します
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
# 最適パラメータを学習器にセット
model.set_params(**best_params)
# 学習曲線の取得
train_sizes, train_scores, valid_scores = learning_curve(estimator=model,
X=X, y=y,
train_sizes=np.linspace(0.1, 1.0, 10),
fit_params=fit_params,
cv=cv, scoring=scoring, n_jobs=-1)
# 学習データ指標の平均±標準偏差を計算
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# 検証データ指標の平均±標準偏差を計算
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(train_sizes, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(train_sizes, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(train_sizes, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(train_sizes, valid_high, valid_low, alpha=0.15, color='green')
# 最高スコアの表示
best_score = valid_center[len(valid_center) - 1]
plt.text(np.amax(train_sizes), valid_low[len(valid_low) - 1], f'best_score={best_score}',
color='black', verticalalignment='top', horizontalalignment='right')
# 軸ラベルおよび凡例の指定
plt.xlabel('training examples') # 学習サンプル数を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
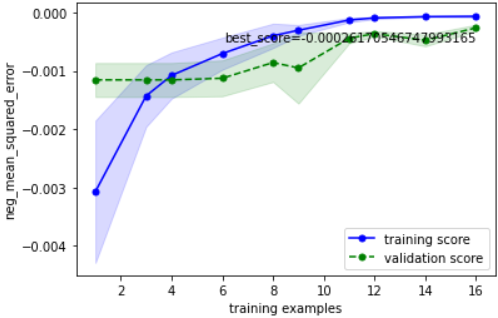
こちらのの確認方法に基づいて確認すると、下記のようにOKと判断できます
・目的の性能を達成しているか → 目標性能は定めていないが、チューニング前より大幅向上(-0.000603 → -0.000262)したのでOKとする
・過学習していないか → データ数が少ない部分では逆転も見られるが、最終的に検証データ指標と学習データ指標が収束しているのでOK
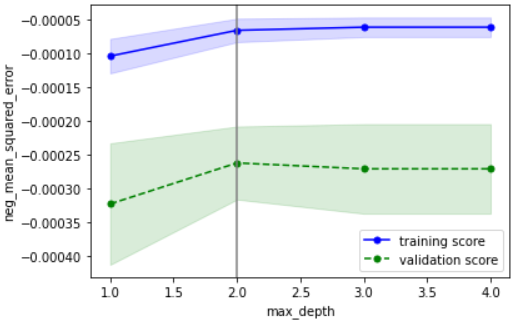
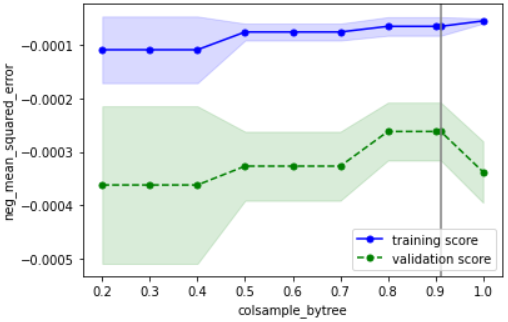
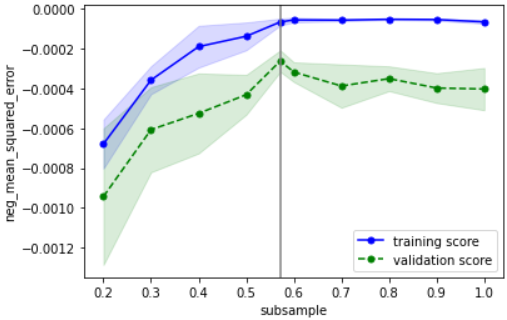
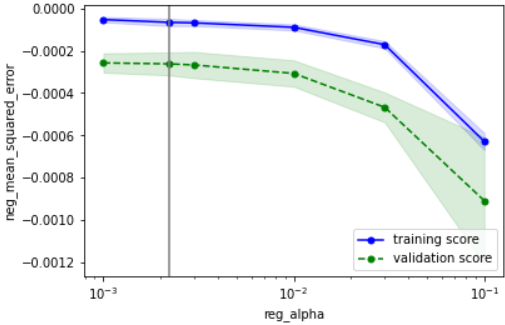
検証曲線
検証曲線をプロットし、
・性能の最大値を捉えられているか
・過学習していないか
を確認します
from sklearn.model_selection import validation_curve
# 検証曲線描画対象パラメータ
valid_curve_params = {'learning_rate': [0.01, 0.02, 0.05, 0.1, 0.2, 0.3],
'min_child_weight': [2, 3, 4, 5, 6, 7, 8],
'max_depth': [1, 2, 3, 4],
'colsample_bytree': [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'subsample': [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
'reg_alpha': [0.001, 0.003, 0.01, 0.03, 0.1],
'reg_lambda': [0.001, 0.003, 0.01, 0.03, 0.1],
'gamma': [0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1]
}
param_scales = {'learning_rate': 'log',
'min_child_weight': 'linear',
'max_depth': 'linear',
'colsample_bytree': 'linear',
'subsample': 'linear',
'reg_alpha': 'log',
'reg_lambda': 'log',
'gamma': 'log'
}
# 最適パラメータを上記描画対象に追加
for k, v in valid_curve_params.items():
if best_params[k] not in v:
v.append(best_params[k])
v.sort()
for i, (k, v) in enumerate(valid_curve_params.items()):
# モデルに最適パラメータを適用
model.set_params(**best_params)
# 検証曲線を描画
train_scores, valid_scores = validation_curve(estimator=model,
X=X, y=y,
param_name=k,
param_range=v,
fit_params=fit_params,
cv=cv, scoring=scoring,
n_jobs=-1)
# 学習データに対するスコアの平均±標準偏差を算出
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# テストデータに対するスコアの平均±標準偏差を算出
valid_mean = np.mean(valid_scores, axis=1)
valid_std = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
# 最適パラメータを縦線表示
plt.axvline(x=best_params[k], color='gray')
# スケールをparam_scalesに合わせて変更
plt.xscale(param_scales[k])
# 軸ラベルおよび凡例の指定
plt.xlabel(k) # パラメータ名を横軸ラベルに
plt.ylabel(scoring) # スコア名を縦軸ラベルに
plt.legend(loc='lower right') # 凡例
# グラフを描画
plt.show()
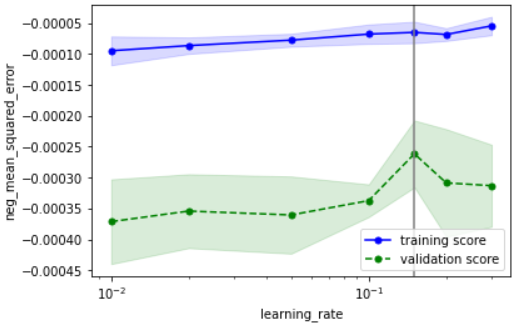
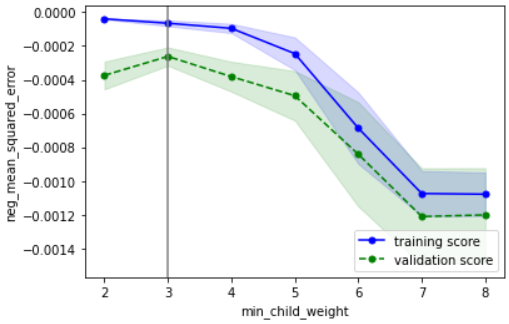
こちらの確認方法に基づいて確認すると、下記のようにOKと判断できます
・性能の最大値を捉えられているか → どのパラメータもだいたい捉えられていそうなのでOKとする
・過学習していないか → データ数が少ないために多少の乖離はあるが、最適パラメータにおいて学習データ指標と検証データ指標が近づいているのでOK
チューニング後のモデルを可視化
最後に、チューニング後のモデルを可視化します(チューニング前と比較)
regplot.regression_heat_plot(model, USE_EXPLANATORY, OBJECTIVE_VARIALBLE, df_osaka,
pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
cv=cv, display_cv_indices=0,
fit_params=fit_params, estimator_params=best_params)
チューニング前より色(予測値)の極端な変化が減り、過学習を防げていそうです。
チューニング成功と言って良いのではと思います。
注意点:XGBoostのチューニング速度について
XGBoostは他の機械学習アルゴリズム(サポートベクター回帰、LightGBMなど)と比べ学習時間が多くかかるため、パラメータチューニングのような学習を繰り返す手法には、多大な時間がかかります(特にデータ数が1000を超えるようなときに顕著)
絶大な効果がある、というほどではないですが、以下の施策がチューニング時間短縮に有効です
・クロスバリデーションの分割数を減らす
・learning_rateの下限を大きく or subsampleの上限を小さく設定(前述)
まとめ
・XGBoostのパラメータチューニングを、8パラメータを選択して実施
・4種類のアルゴリズムのうち、Optunaが速度、評価指標両方で最も優れていた
・パラメータのうち、learning_rateの下限が低い時 or subsampleの上限が高いときは学習速度が遅くなる