今回は scikit-learn の 線形モデルを使った回帰を試してみます。
線形モデルの予測式
線形モデルの一般的な予測式は以下のようになります。
y = w * x + b
ここで、w は 特徴量 x に対する「重み」を b は「バイアス」を表し、
直線の数式として考えると、それぞれ「傾き」と「切片」に該当します。
又、特徴量が1つの場合は単回帰での予測式となり、
特徴量が複数ある場合は以下のような式となり、重回帰での予測式となります。
y = \sum_{i=1}^{n} (w_{i}x_{i}) + b = w_1x_1 + w_2x_2 \cdots + w_nx_n + b
線形回帰(最小二乗法)
予測値と正解値の平均二乗誤差を「損失関数」として使い、
この「損失関数」の結果が最小になるような「重み」と「バイアス」を求めます。
平均二乗誤差(Mean Squared Error)
正解値と予測値の差を二乗し、平均をとったものになります。
MSE(y_i, \hat{y_i}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2\\
y_i:正解値 \hat{y_i}:予測値
クラス
sklearn.linear_model.LinearRegression クラスを使用します。
インポート
必要なものを予めインポートしておきます。
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
トレーニング・予測・評価
ボストン住宅価格データを利用して、トレーニング・予測・評価を行います。
特徴量は「部屋数」のみを使用します(単回帰)
########################
# 線形回帰(最小二乗法)
########################
from sklearn.linear_model import LinearRegression
from sklearn import datasets
# データセットロード
boston = datasets.load_boston()
# 特徴量
X = boston.data[:, [5]] # 部屋数
# 目的変数
Y = boston.target
# トレーニング・テストデータ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
# LinearRegression
lr = LinearRegression()
lr.fit(X_train, Y_train)
# 予測
Y_pred = lr.predict(X_test)
#
# 評価
#
# 平均絶対誤差(MAE)
mae = mean_absolute_error(Y_test, Y_pred)
# 平方根平均二乗誤差(RMSE)
rmse = np.sqrt(mean_squared_error(Y_test, Y_pred))
# スコア
score = lr.score(X_test, Y_test)
print("MAE = %.2f, RMSE = %.2f, score = %.2f" % (mae, rmse, score))
print("Coef = ", lr.coef_)
print("Intercept =", lr.intercept_)
結果は以下のようになりました。
coef_ は「重み」、intercept_ は「バイアス」になります。
MAE = 4.21, RMSE = 6.59, score = 0.47
Coef = [9.31294923]
Intercept = -36.180992646339206
・平均絶対誤差(MAE)
正解値と予測値の差分の絶対値を平均したもの
・平方根平均二乗誤差(RMSE)
正解値と予測値の差分の二乗を平均し、平方したもの
また、この結果を予測式として表すと以下のようになります。
※ x に数値を入れることで 予測結果 y が求まります。
y = 9.31294923 * x + (-36.180992646339206)
プロット
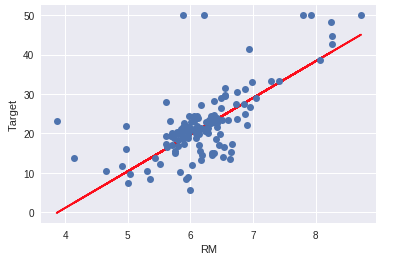
テストデータ上での正解値(青)と予測値(赤)をプロットします。
部屋数の増加に伴い、予測値が上昇している事がわかります。
plt.xlabel("RM")
plt.ylabel("Target")
plt.plot(X_test, Y_pred, "r-")
plt.plot(X_test, Y_test, "o")
特徴量を増やす
特徴量のコードを以下のように修正して、トレーニング・予測・評価を行ってみます。
特徴量が複数(13)となるため、重回帰となります。
# 特徴量
X = boston.data # 全て
13個の「重み」が出力されました。
予測精度が少し上がっています。
MAE = 3.67, RMSE = 5.46, score = 0.64
Coef = [-1.16869578e-01 4.39939421e-02 -5.34808462e-03 2.39455391e+00
-1.56298371e+01 3.76145473e+00 -6.95007160e-03 -1.43520477e+00
2.39755946e-01 -1.12937318e-02 -9.86626289e-01 8.55687565e-03
-5.00029440e-01]
Intercept = 36.980455337620576
リッジ回帰
リッジ回帰とは
・基本は通常の線形回帰
・過学習を抑制するために重みに対してペナルティが与えられる
・ペナルティには L2 正則化 が使われる
・突出した重みが出にくくなる
・トレーニングデータが少ない場合に有効
・トレーニングデータが大量にある場合には効果が薄くなる
L2 正則化
ペナルティとして、以下の正則化項(二乗和)を「損失関数」に付加する。
\lambda \sum_{i=1}^{n} w_i^2 \\
\lambda(ラムダ):ハイパーパラメータ
この正則化項を線形回帰の「損失関数」に付加することで、大きな重みを取ることへのペナルティを与えます。
また、λ はハイパーパラメータとなり、λの値を大きくすることでペナルティを強めることが出来ます。
\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 + \lambda \sum_{i=1}^{n} W_i^2 \\
y_i:正解値 \hat{y_i}:予測値
クラス
sklearn.linear_model.Ridge クラスを使用します。
トレーニング・予測・評価
ボストン住宅価格データを利用して、トレーニング・予測・評価を行います。
(特徴量は1つ、部屋数のみを使用します)
又、alpha値が正則化項の λ にあたるハイパーパラメータとなり、
値を大きくすることでペナルティが強くなります。
以下は、alpha値を 0.1〜100 まで増加させた場合の重みとスコアの変化を確認するコードになります。
########################
# リッジ回帰
########################
from sklearn.linear_model import Ridge
from sklearn import datasets
boston = datasets.load_boston()
# 特徴量
X = boston.data[:, [5]] # 部屋数
# 目的変数
Y = boston.target
# トレーニング・テストデータ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
list_alpha = [n*0.1 for n in range(1, 1001)]
list_coef = []
list_score = []
for alpha_val in list_alpha:
# Ridge
ridge = Ridge(alpha=alpha_val)
ridge.fit(X_train, Y_train)
# 予測
Y_pred = ridge.predict(X_test)
# スコア
score = ridge.score(X_test, Y_test)
list_coef.append(ridge.coef_)
list_score.append(score)
plt.figure(figsize=(18, 7))
plt.subplot(1, 2, 1)
plt.title("Alpha vs Coef", fontweight="bold", size=18)
plt.xlabel("alpha")
plt.ylabel("Coef")
plt.ylim(0, 10)
plt.plot(list_alpha, list_coef, "-b")
plt.subplot(1, 2, 2)
plt.title("Alpha vs Score", fontweight="bold", size=18)
plt.xlabel("alpha")
plt.ylabel("Score")
plt.ylim(0, 1)
plt.plot(list_alpha, list_score, "-g")
plt.show()
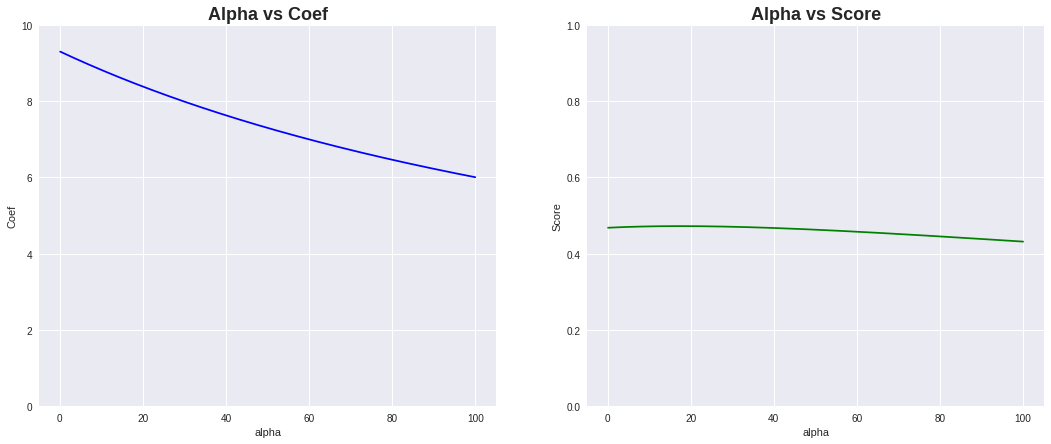
プロットを見てみると alpha値の増加により重みが小さくなる事が確認出来ます。
スコアは、少し上がった後下がっています。
重みが小さくなり、若干アンダーフィッティングが発生しているようです。
トレーニングデータの増減によるリッジ回帰と通常の線形回帰の比較
トレーニングデータを 50〜500件まで変化させ、そのスコアをプロットしてみます。
データセットは、sklearn.datasets.make_regressionクラスを使って生成しました。
※特徴量の数(n_features)を 100、相関関係のある特徴量の数(n_informative)を 5 に設定しています。
from sklearn.datasets import make_regression
ridge_train_score = []
ridge_score = []
lr_train_score = []
lr_score = []
sample_num_list = range(50, 501, 10) # [50, 60, 70 ... 500]
for sample_num in sample_num_list:
# データセット生成
X, Y = make_regression(random_state=12,
n_samples=sample_num,
n_features=100,
n_informative=5,
noise=50.0)
# トレーニング・テストデータ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
# トレーニング
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, Y_train)
lr = LinearRegression()
lr.fit(X_train, Y_train)
# スコア
ridge_train_score.append(ridge.score(X_train, Y_train))
ridge_score.append(ridge.score(X_test, Y_test))
lr_train_score.append(lr.score(X_train, Y_train))
lr_score.append(lr.score(X_test, Y_test))
# プロット
plt.figure(figsize=(15, 7))
plt.title("Ridge vs LinearRegression", fontweight="bold", size=18)
plt.plot(sample_num_list, ridge_train_score, 'y--', label="Ridge Train")
plt.plot(sample_num_list, ridge_score, "g", label="Ridge Test")
plt.plot(sample_num_list, lr_train_score, 'c--', label="LinearRegression Train")
plt.plot(sample_num_list, lr_score, "b", label="LinearRegression Test")
plt.ylim(0, 1.0)
plt.xlabel('Number of sample data')
plt.ylabel('Score')
plt.legend()
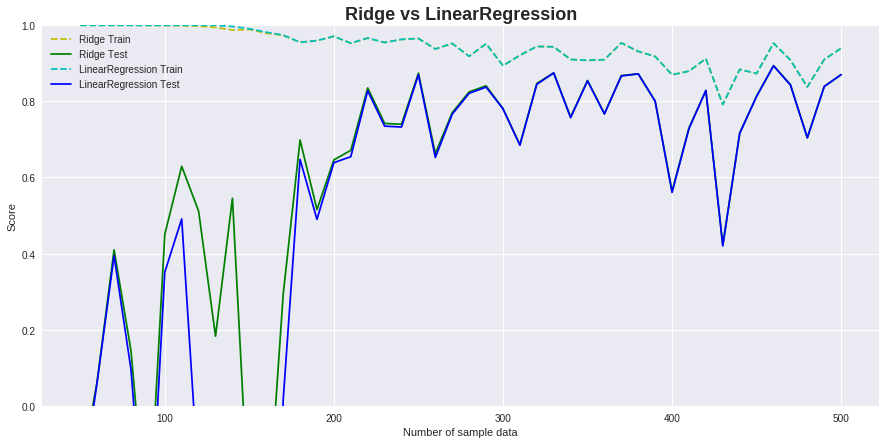
プロットを確認してみると、データ件数が少ない箇所では、
通常の線形回帰より精度が出ており過学習も抑制されています。
トレーニングデータが少ない場合に有効という特性を確認出来ました。
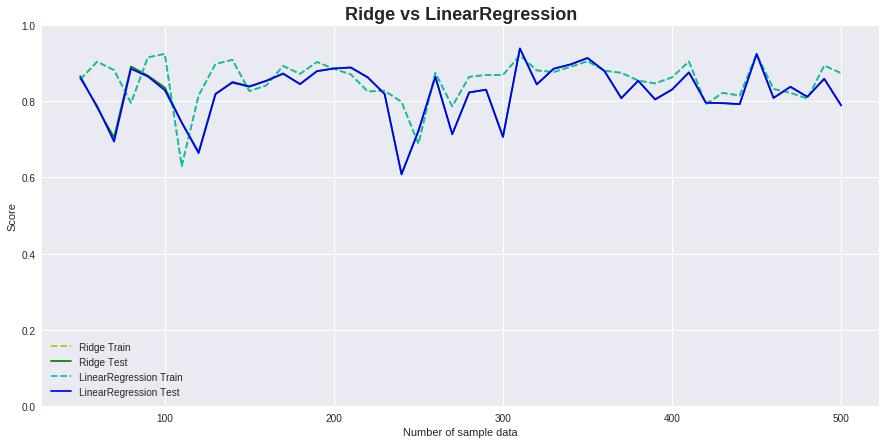
また、特徴量の数を少なく(10)に設定した場合は、通常の線形回帰と変化はありませんでした。
これは特徴量の数が少ない場合には、過学習が起きにくいためと思われます。
Lasso
Lassoとは
・基本は通常の線形回帰
・過学習を抑制するために重みに対してペナルティが与えられる
・ペナルティには L1 正則化 が使われる
・いくつかの重みが完全に0となる
・重みが0となった特徴量の入力は無視される
・特徴量が多く、重要なものがわずかしかないと予想される場合に向いている
L1 正則化
ペナルティとして以下の正則化項(絶対値の和)を「損失関数」に付加する。
\lambda \sum_{i=1}^{n} |w_i| \\
\lambda(ラムダ):ハイパーパラメータ
リッジ回帰と同様、この正則化項を線形回帰の「損失関数」に付加することで、大きな重みを取ることへのペナルティを与えます。
また、λ はハイパーパラメータとなり、λの値を大きくすることでペナルティを強めることが出来ます。
\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 + \lambda \sum_{i=1}^{n} W_i^2 \\
y_i:正解値 \hat{y_i}:予測値
クラス
sklearn.linear_model.Lasso クラスを使用します。
トレーニング・予測・評価
ボストン住宅価格データを利用して、トレーニング・予測・評価を行います。
以下は、alpha値を 0.1、1.0、10 まで増加させた場合の重みの変化を確認するコードになります。
########################
# Lasso
########################
from sklearn.linear_model import Lasso
from sklearn import datasets
boston = datasets.load_boston()
# 特徴量
X = boston.data
# 目的変数
Y = boston.target
# トレーニング・テストデータ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
coef_list = []
alpha_list = [0.1, 1.0, 10]
for alpha_val in alpha_list: # alpha値:初期値1.0
# Ridge
lasso = Lasso(alpha=alpha_val)
lasso.fit(X_train, Y_train)
# 予測
Y_pred = lasso.predict(X_test)
#
# 評価
#
# 平均絶対誤差(MAE)
mae = mean_absolute_error(Y_test, Y_pred)
# 平方根平均二乗誤差(RMSE)
rmse = np.sqrt(mean_squared_error(Y_test, Y_pred))
# スコア
score = lasso.score(X_test, Y_test)
coef_list.append(lasso.coef_)
print("[alpha=%.1f] MAE = %.2f, RMSE = %.2f, score = %.2f" % (alpha_val, mae, rmse, score))
print(" Coef =", lasso.coef_)
print(" Intercept =", lasso.intercept_)
print(" Number without the Weight =", np.sum(lasso.coef_ == 0))
実行結果
いくつかの重みが完全に0になっています。
[alpha=0.1] MAE = 3.74, RMSE = 5.67, score = 0.61
Coef = [-0.10830419 0.04682671 -0.05211898 0.76930234 -0. 3.62459196
-0.01775549 -1.17784084 0.20089449 -0.01298688 -0.8272527 0.00947862
-0.53793915]
Intercept = 27.730698520522022
Number without the Weight = 1
[alpha=1.0] MAE = 4.03, RMSE = 6.05, score = 0.55
Coef = [-0.05921813 0.05001375 -0.00155282 0. -0. 0.75853268
0.01305146 -0.71049912 0.19577234 -0.01414816 -0.80558201 0.00715616
-0.74231187]
Intercept = 44.7377215472102
Number without the Weight = 2
[alpha=10.0] MAE = 4.64, RMSE = 7.01, score = 0.40
Coef = [-0. 0.03268736 -0. 0. 0. 0.
0. -0. 0. -0.01155886 -0. 0.00679307
-0.54971232]
Intercept = 31.341265970206273
Number without the Weight = 9
プロット
重みをプロットします。
def feature_plt(data: np.ndarray,
feature_names: np.ndarray,
coef_: np.ndarray,
title: str):
plt.figure(figsize=(8, 5))
plt.title(title, fontweight="bold", size=18)
plt.plot(coef_.T, 'o')
plt.ylim(-2, 4)
plt.xticks(range(data.shape[1]), feature_names, rotation=90)
plt.hlines(0, 0, data.shape[1])
for i, coef in enumerate(coef_list):
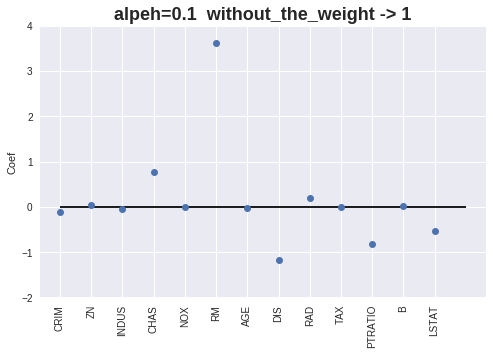
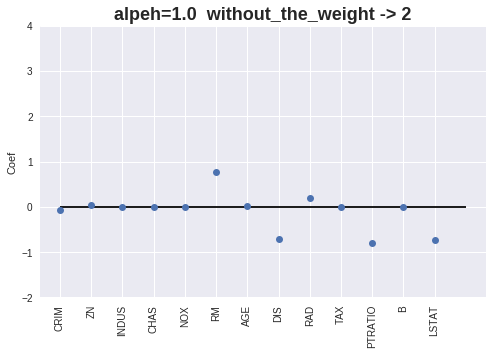
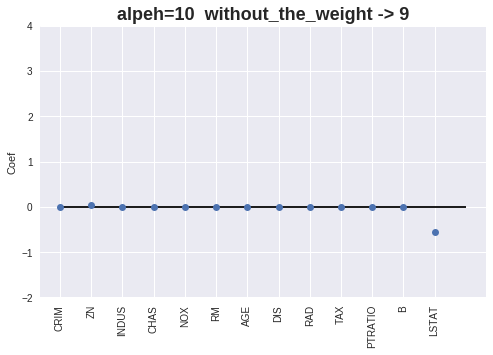
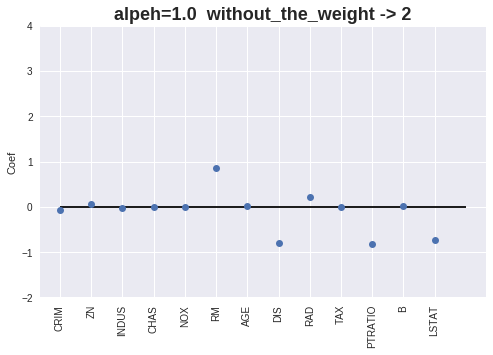
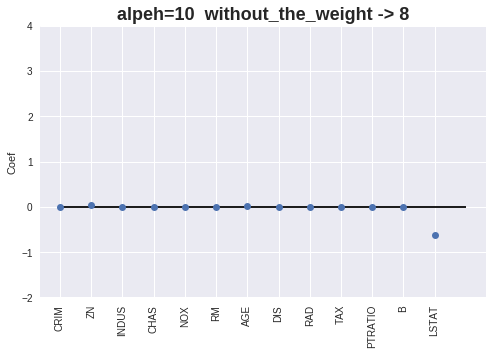
feature_plt(boston.data, boston.feature_names, coef, "alpeh=%s without_the_weight -> %d" % (alpha_list[i], np.sum(coef == 0)))
alpha値が増加すると、重みが0となる特徴量が増える事が確認出来ます。
ElasticNet
リッジ回帰とLassoが組み合わさった回帰となります。
・基本は通常の線形回帰
・過学習を抑制するために重みに対してペナルティが与えられる
・正則化としての L1 と L2 が組み合わされたもの
クラス
sklearn.linear_model.ElasticNet クラスを使用します。
トレーニング・予測・評価
ボストン住宅価格データを利用して、トレーニング・予測・評価を行います。
以下は、alpha値を 0.1、1.0、10 まで増加させた場合の重みの変化を確認するコードになります。
########################
# ElasticNet
########################
from sklearn.linear_model import ElasticNet
from sklearn import datasets
boston = datasets.load_boston()
# 特徴量
X = boston.data
# 目的変数
Y = boston.target
# トレーニング・テストデータ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
coef_list = []
alpha_list = [0.1, 1.0, 10]
for alpha_val in alpha_list: # alpha値:初期値1.0
# Ridge
lasso = ElasticNet(alpha=alpha_val)
lasso.fit(X_train, Y_train)
# 予測
Y_pred = lasso.predict(X_test)
#
# 評価
#
# 平均絶対誤差(MAE)
mae = mean_absolute_error(Y_test, Y_pred)
# 平方根平均二乗誤差(RMSE)
rmse = np.sqrt(mean_squared_error(Y_test, Y_pred))
# スコア
score = lasso.score(X_test, Y_test)
coef_list.append(lasso.coef_)
print("[alpha=%.1f] MAE = %.2f, RMSE = %.2f, score = %.2f" % (alpha_val, mae, rmse, score))
print(" Coef =", lasso.coef_)
print(" Intercept =", lasso.intercept_)
print(" Number without the Weight =", np.sum(lasso.coef_ == 0))
実行結果は以下のようになりました。
[alpha=0.1] MAE = 3.77, RMSE = 5.68, score = 0.61
Coef = [-0.10868369 0.04944529 -0.06152394 0.89220243 -0. 3.167248
-0.01531596 -1.20462522 0.21321796 -0.01330742 -0.84528602 0.00916648
-0.56772562]
Intercept = 31.450143616264054
Number without the Weight = 1
[alpha=1.0] MAE = 4.00, RMSE = 5.99, score = 0.56
Coef = [-0.07852654 0.05269712 -0.03077338 0. -0. 0.86719889
0.0125003 -0.80505201 0.225549 -0.01468779 -0.81006507 0.00746296
-0.72784018]
Intercept = 44.533233738212026
Number without the Weight = 2
[alpha=10.0] MAE = 4.58, RMSE = 6.88, score = 0.42
Coef = [-0. 0.04570394 -0. 0. 0. 0.
0.01759221 -0. 0. -0.01113388 -0. 0.00647568
-0.61765624]
Intercept = 30.772621565404812
Number without the Weight = 8
プロット
重みをプロットします。
def feature_plt(data: np.ndarray,
feature_names: np.ndarray,
coef_: np.ndarray,
title: str):
plt.figure(figsize=(8, 5))
plt.title(title, fontweight="bold", size=18)
plt.plot(coef_.T, 'o')
plt.ylim(-2, 4)
plt.xticks(range(data.shape[1]), feature_names, rotation=90)
plt.hlines(0, 0, data.shape[1])
for i, coef in enumerate(coef_list):
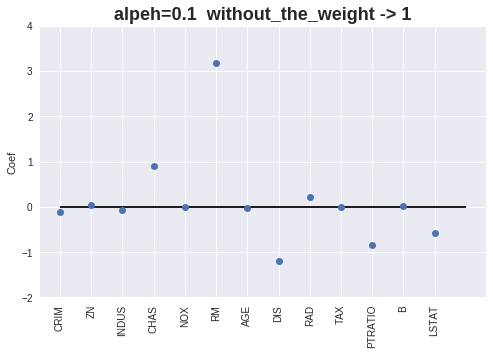
feature_plt(boston.data, boston.feature_names, coef, "alpeh=%s without_the_weight -> %d" % (alpha_list[i], np.sum(coef == 0)))
重みが0の特徴量が多く出力されますが、Lasso を使用時よりは若干少なくなりました。
以上、scikit-learn の 線形モデルを使った回帰を試してみました。