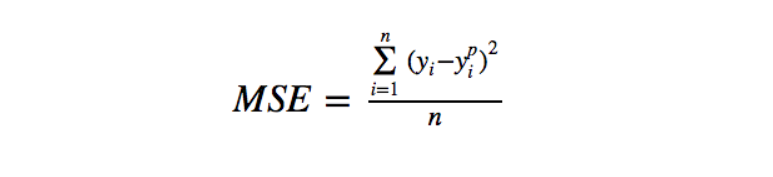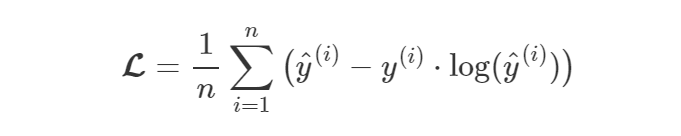目次##
- 平均絶対誤差 (MAE)
- 平均二乗誤差 (MSE)
- Huber損失
- Log-cosh損失
- Poisson損失
- Hinge損失
- Custom-Loss関数
間違いがあったら下のコメントか編集リクエストを頂けると有難いです。
平均絶対誤差 (MAE)##
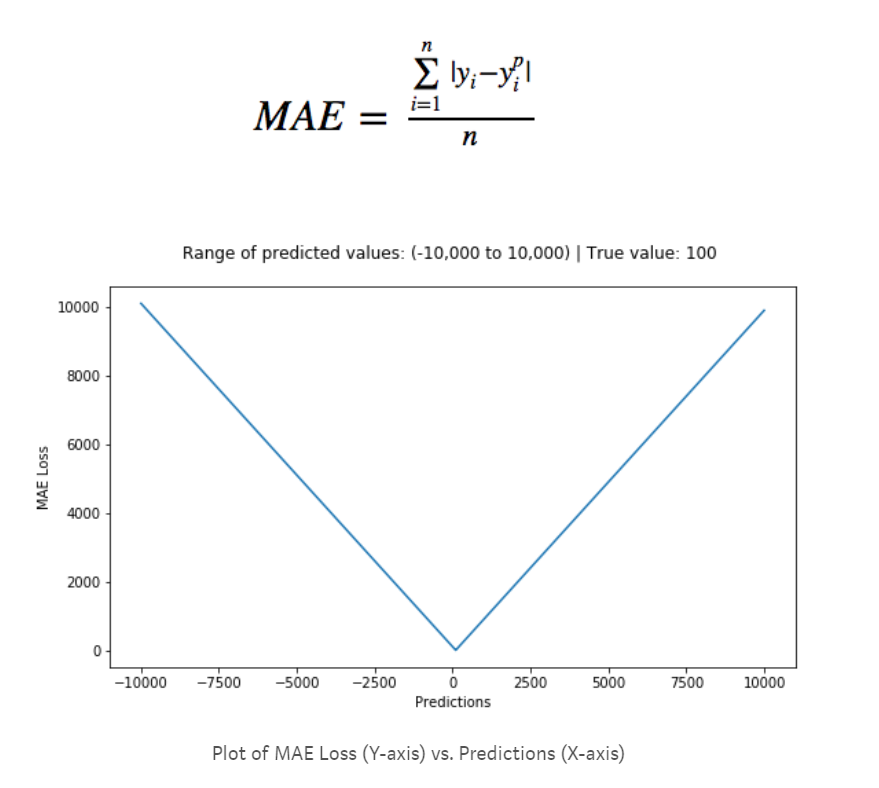
引用元:https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0
(上図はMAEの微分をプロットしている)
詳しくはMSEの項目で説明するが、MAEの一つの特徴として外れ値に寛容なことが言える。損失を二乗しないのでMSEのように外れ値のときの損失がそこまで大きくならないからだ。
MAEには損失関数の微分が常に一定になるという問題がある。これは損失がどのような値であっても同じスピードで損失を埋めることを意味する。損失が小さいときに損失が大きいときと同じスピードで学習されては最適化できないだろう。損失が小さいとき、つまりモデルが細かい調整をするときはゆっくりと学習させるべきである。これはlearning_rateを予め小さく設定すること実現できるがベストとは言えない。
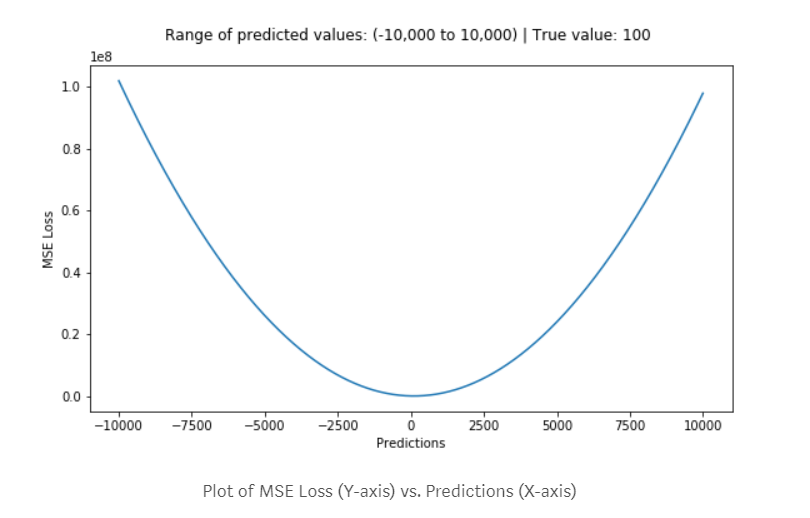
平均二乗誤差 (MSE)##
(上図はMSEの微分をプロットしている)
MAEは外れ値に寛容であったのに対し、MSEは寛容ではない。これは予測値と実測値の差を二乗しているからである。例えばMAEの損失が3だとするとMSEは9になる。ここでもしMAEの損失を大きくして(外れ値は損失が大きい)30とするとMSEは900になる。このことからMSEは外れ値に寛容でなく外れ値から大きく学習しようとする性質があることが分かる。このことはMAEがデータの中央値寄りなのに対し、MSEは平均値に近いと考えると分かりやすいだろう。ではどちらを選ぶべきか。もしも外れ値がビジネス的な立ち位置で重要な場合はMSEを選ぶべきだろう。ちゃんと外れ値からの損失をモデルに組み込もうとしてくれるからである。ただしこの場合、他のデータの予測能力が劣ることも視野に入れなければならない。逆に外れ値がそこまで重要でない(ノイズに近い)データの場合はMAEを使うべきである。ただし外れ値が完全なノイズの場合は外れ値をデータから除去してMSEを使うべきである。
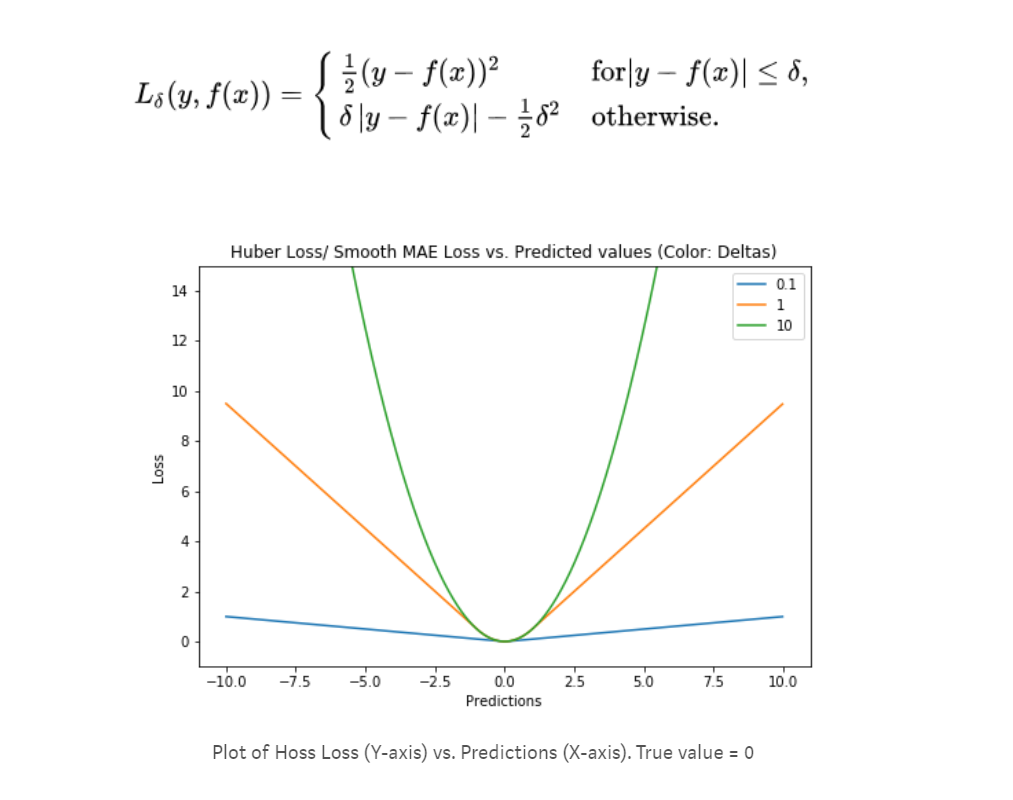
Huber Loss##
Huber Lossとは損失が大きいとMAEに似た機能をし、損失が小さいとMSEの機能になる。MAEとMSEの良いとこどりである。その機能通りSmooth Absolute Lossとも言われている。このMSEとMAEの切り替わりは𝛿で設定する。これにより外れ値に寛容でありながらMAEの欠点を克服できる。
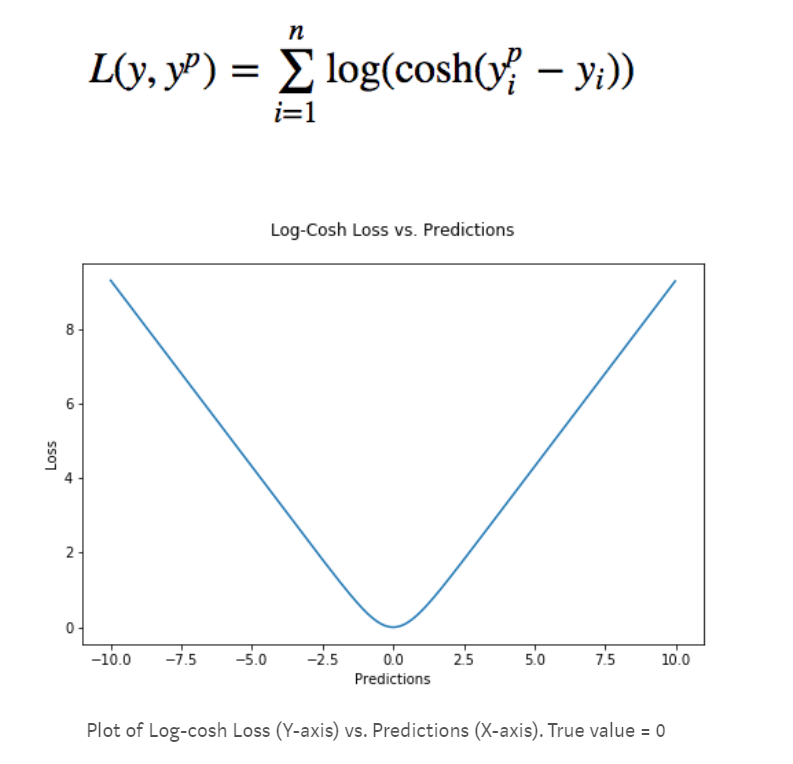
Log-cosh Loss##
Huber Lossと同じように、基本MAEだが損失が小さくなるとMSEに近くなる。マクローリン展開により$cosh(x)=e^\frac{x^2}{2}$。よって$log(cosh(x))$はxが0に近いとき$\frac{x^2}{2}$と同じような動きをする。逆にxが大きいときはテイラー展開により$abs(x)-log(2)$に近い動きをする。
もう一つの利点は2回微分可能であることだ。なぜ2回微分可能が良いのか。それはGBDTは基本ニュートン法で最適な値を探すからである。2回微分可能であれば、ある種のモメンタム(運動量、勢い)をモデルに学習させることができる。
ポアソン損失 (Poisson Loss)##
主にカウントデータで使われる。ポアソン分布が元である。ポアソン分布とはX軸をとある事象が起こる数、Y軸をその夫々の回数が起こる確率とを表す分布である。
予測値の分布とポアソン分布の損失がポアソン損失である。
ヒンジ損失 (Hinge Loss)##
ヒンジ損失に関してはこのサイトが分かりやすい。
f_1(x) = \left\{
\begin{array}{ll}
0 & (x \leq 0) \\
x-a & (x > a)
\end{array}
\right.
上の式は下の式と同等である。
f_1(x) = max(0,x-a)
この式も
f_2(x) = \left\{
\begin{array}{ll}
b-x & (x \leq b) \\
0 & (x > 0)
\end{array}
\right.
以下と同じである。
f_2(x) = max(0,b-x)
よってこれらを合わせると以下の等式になる。
t = ±1 \\
L(y) = max(0, 1-t*y)
ヒンジ損失はSVM等で使われる。
Custom Loss Function##
ライブラリに無い関数はcustom loss functionとして自分で設定が可能だ。この場合gradとhessianを返り値とする必要がある。hessianとは二次導関数のことである。以下はlog-cosh損失の実装だ。
def logcoshobj(preds, dtrain):
labels = dtrain.get_label()
grad = np.tanh(preds - labels) #log-coshを微分→tanh(予測値-ラベル値)
hess = 1.0 - grad*grad
return grad, hess
引用:https://www.kaggle.com/c/allstate-claims-severity/discussion/24520
なおobjective=logcoshobjと設定する必要がある。
eval_metricをカスタム関数としたい場合は以下のようにする。
def accuracy(preds, train_data):
labels = train_data.get_label()
# 返り値は「出力したいmetricの名前」「損失値」「そのメトリックが高くなればモデルも良くなるかの真偽値
return 'customed_accuracy', np.mean(labels == (preds > 0.5)), True
3個目の返り値について例えばaccuracyであればTrueだし、loglossなどの損失関数ならばFalseである。
なお、feval=accuracyと設定する必要がある。
参考文献##
http://www.cs.cornell.edu/courses/cs4780/2015fa/web/lecturenotes/lecturenote10.html
http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0