2019/2/13
Qiita初投稿です.
[追記]
英語ですが,より詳しい説明をarXivにUploadしました.
長くなってしまったので,投稿を分離しました.
Optunaのアルゴリズムは追ってみたいが,コード長過ぎるよ...
という人が参照すべきコード.冗長なコードを簡潔にし,変数名の統一性が取れるようにリファクタリングしました.行数はOptunaと比較してだいぶ減っています.
自作したTPE
注意: 以前に加えた性能向上のための変更により,本記事の説明とは異なる多変量のモデルに関する実装コードでかつ突然変異のHeuristicsが入っています.
Prefered Networks(PFN)から発表されたOptunaが利用しているモデル(TPE)のコードを読んでみたので自分の持つ知識内でまとめてみました.枝刈の部分については記載していません.OptunaではSuccessive Halvingという手法を使用していますが,現在は学習曲線の予測の研究も各所で行われているので,今後それらの内容が導入されてくるのでは,と思っています.
[2020年9月10日追記]
学習曲線予測モデルのPRを投稿しました.
ちなみにOptunaの元はHyperoptでその論文がこちらとこちらが続報.TPEのアルゴリズムはOptunaとHyperoptでほぼほぼ変わってないです.最近は開発が進み新たな機能がどんどん追加されており,細かな実装は異なってきています.ただし,メインで使われているアルゴリズム自体は変わっていません.
手法を説明しているその他のページ
・hyperoptって何してんの?
なお,使用方法に関しては以下のリンクを参照にしてください.
・GridSearchCVはもう古い!Optunaでサポートベクターマシンもラクラクチューニング
・Optunaでハイパーパラメータチューニング
・optunaによるrandom forestのハイパーパラメータ最適化
ハイパパラメータ最適化
機械学習等では学習率,重み減衰率,慣性項等事前に設定すべきパラメータがあり,それらをハイパパラメータと呼ぶ.一般的にハイパパラメータの数の指数オーダーで探索すべき空間が増えるため,特に専門家でない方にとってはハイパパラメータを決定することが難しい.その課題を解決する手段を提案するのがハイパパラメータ最適化.
ハイパパラメータ最適化の代表例
グリッドサーチ ・ ランダムサーチ
最も有名な手法として上の2つがある.問題点は探索に時間がかかることで,特にグリッドサーチは引用先が示している通り,性能に対してあまり影響を及ぼさない変数に対しても真面目に探索するため時間がかかりすぎるという問題点がある.
CMA-ES
進化計算の一種で昨今の進化計算モデルでは最も性能が良いとされている.ただし,ハイパパラメータ最適化の界隈ではベイズ最適化ほどの人気はない.個人的には進化計算が直感的にうまく行きそうな気がしているが,画像認識ではあまり結果が出ていないらしい.(手法自体のハイパパラメータ調整が難しいから?)
Nelder-Mead法
画像認識に対して有効な手法としてNelder-Mead法がある.こちらの論文では以下で説明するTPEよりも良い性能を出す可能性があることを示唆している.ただし,TPEとの違いは幾何学的な探索なのでcategoricalやconditionalなハイパパラメータの探索に弱い.
ベイズ最適化
最適化界隈で熱い手法.多くの論文はこれに関するもの(2019年1月現在).観測点から確率的に良質な点を予測する手法で,確率的な予測を何によって行うかがこの手法のカギを握っている.現状,Gaussian Process(ガウス過程:GP)が広く用いられている.ガウス過程はざっくり言うと探索空間内のある点の平均値と分散を今までの観測点から決定し,その点では評価値がその平均と分散に従った正規分布に従うというもの.空間内の候補点(主にCMA-ESを用いて決める)の内,獲得関数の値が良いものを選択し実際に予測を行う.(詳しくは他のページを参照してください.)
TPE (Tree-Structured Parzen Estimator)
TPEのすごさ
出典に示されている論文によると最近のハイパパラメータ探索手法の中では最も良い結果を出している(1つ目の図).また,12回の探索を通して平均的に結果が良く,結果のばらつきが少なかったのがTPE(2つ目の図).一方でばらつきを考慮すると最高の結果を出したのはNelder-Mead法だったりする.
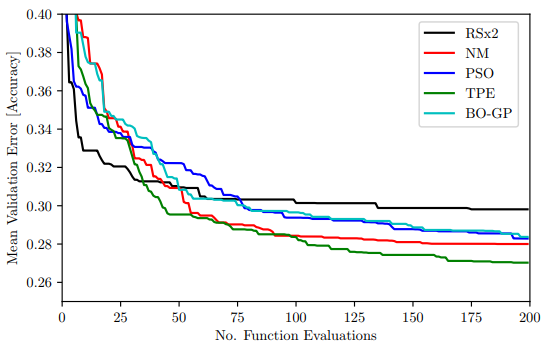
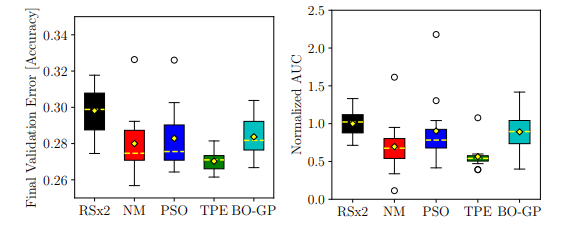
出典:A Comparative Study of Black-box
Optimization Algorithms for Tuning of
Hyper-parameters in Deep Neural Networks
アルゴリズム概説
Optunaで用いられているTPEもベイズ最適化の一種.観測点から確率的に良質な点を探索するという考え方は変わらない.しかしながら,ガウス過程のときはハイパパラメータ同士の相関関係を考慮して関数をモデル化しているが,こちらのモデルでは全てのハイパパラメータに対して独立を仮定して確率密度関数の推定を行う.
評価値の最小化の場合
1.観測点を上位 $\gamma$ %の評価値を基準として2つの集合 $G$(greater), $L$(lower)に分割する
2.G,Lそれぞれの集合に対して,ハイパパラメータごとに $G$ に属する確率密度関数 $g(x)$,$L$に属する確率密度関数 $l(x)$ をカーネル密度推定する
3.ハイパパラメータごとにLの確率密度関数に従った疑似乱数を生成し,その疑似乱数に対して獲得関数を変形した関数 $\frac{l(x)}{g(x)}$ の値を求め,良い値のときの引数 $x$ を採択する
手法名の由来
一応,論文から名前の意図を読み取ると,
・Tree-structured
Introductionによると,
"In this work we restrict ourselves to tree-structured configuration spaces. Configuration spaces are tree-structured in the sense that some leaf variables (e.g. the number of hidden units in the 2nd layer of a DBN) are only well-defined when node variables (e.g. a discrete choice of how many layers to use) take particular values."
とのことなので,選ばれたハイパパラメータによって,評価する必要のないハイパパラメータが生じ,TPEではこのようなConditionalなハイパパラメータを木構造空間で管理する.
・Parzen Estimator
カーネル密度推定のことを指している.観測点から各ハイパパラメータの確率密度関数をカーネル密度推定で推定する.